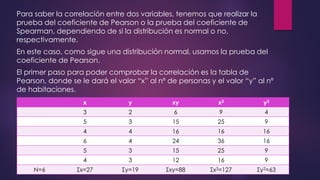
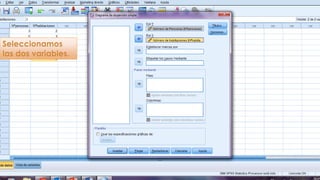
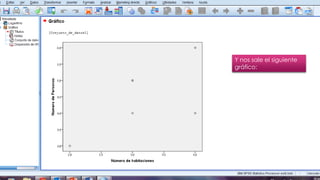
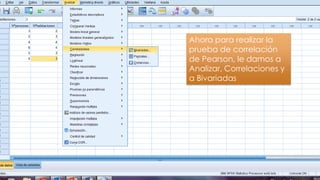
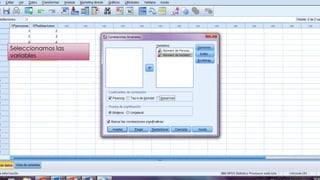
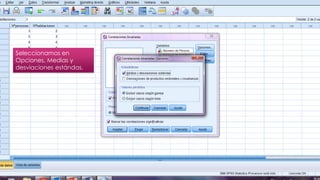
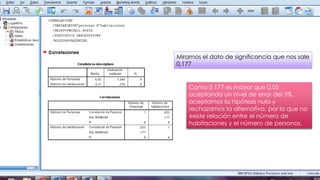
Este documento resume los pasos para analizar la correlación entre el número de personas que habitan en un hogar y el número de habitaciones del mismo usando el coeficiente de Pearson. Calcula un coeficiente de correlación de 0.633 pero determina que no es estadísticamente significativo dado que el valor p de 0.177 es mayor que 0.05, por lo que no existe evidencia de una relación entre las dos variables.

1. LORENA BORJA HERRERA
UNIDAD DOCENTE DE VALME. GRUPO 1

2. En un municipio español se ha realizado una
pequeña encuesta que ha preguntado por el nº de
personas que habitan en un hogar y el nº de
habitaciones del mismo.
Si ambas variables se distribuyen normalmente:
1. Averiguar si existe correlación entre ambas variables en la población de
donde derivan los datos. Calcular el coef. De correlación de Pearson.
2. Averiguar si el coeficiente de correlación es significativo. Realizar las
hipótesis.
3. Incluir los datos en SSPS y realizar gráfico dispersión simple, realizar la
correlación de Pearson y evaluar los resultados.

3. Para saber la correlación entre dos variables, tenemos que realizar la
prueba del coeficiente de Pearson o la prueba del coeficiente de
Spearman, dependiendo de si la distribución es normal o no,
respectivamente.
En este caso, como sigue una distribución normal, usamos la prueba del
coeficiente de Pearson.
El primer paso para poder comprobar la correlación es la tabla de
Pearson, donde se le dará el valor “x” al nº de personas y el valor “y” al nº
de habitaciones.
x y xy x2 y2
3 2 6 9 4
5 3 15 25 9
4 4 16 16 16
6 4 24 36 16
5 3 15 25 9
4 3 12 16 9
N=6 Σx=27 Σy=19 Σxy=88 Σx2=127 Σy2=63

4. Ahora que ya tenemos los datos suficientes para poder
realizar el coeficiente de Pearson, lo hacemos:
(𝟔 · 𝟖𝟖) − (𝟐𝟕 · 𝟏𝟗)
𝟔 · 𝟏𝟐𝟕 − 𝟐𝟕 𝟐)( 𝟔 · 𝟔𝟑 − 𝟏𝟗 𝟐)
=
𝟓𝟐𝟖 − 𝟓𝟏𝟑
𝟓𝟔𝟏
= 𝟎, 𝟔𝟑𝟑

5. Ahora, una vez que hemos obtenido la información y hemos sacado que existe
una correlación entre las dos variables, queremos saber si esa correlación es
verdadera o es debida al azar. Para ello realizamos la prueba de la T de
Student:
𝑡(𝑛−2) = 𝑟 𝑥𝑦 (𝑛 − 2)/(1 − (𝑟 𝑥𝑦
)2
= 0,63 (6 − 2)/(1 − 0,63 2 = 0,63
Ahora comparamos la t real con la de la tabla. Para ello necesitamos el grado de libertad que es
(N-2)=4 y el nivel de significancia que es 0,05. En la tabla sale 2,1318.
Ho= No existe relación entre el número de habitación y el de personas.
H1= Existe relación entre el número de habitación y de personas.
Solución: como t real < t tabla, se rechaza la hipótesis alternativa y se acepta la hipótesis nula,
por lo que no existe relación entre en número de personas y el número de habitaciones.

8. Pasa saber la dispersión, le
damos a Gráficos, Cuadros
de diálogo antiguos y a
Dispersión/Puntos.

9. Seleccionamos
Dispersión simple.

11. Y nos sale el siguiente
gráfico:

12. Ahora para realizar la
prueba de correlación
de Pearson, le damos a
Analizar, Correlaciones y
a Bivariadas

13. Seleccionamos las
variables

14. Seleccionamos en
Opciones, Medias y
desviaciones estándas.

15. Miramos el dato de significancia que nos sale
0,177
Como 0,177 es mayor que 0,05
aceptando un nivel de error del 5%,
aceptamos la hipótesis nula y
rechazamos la alternativa, por lo que no
existe relación entre el número de
habitaciones y el número de personas.