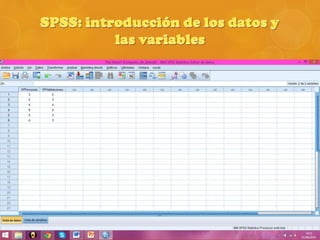
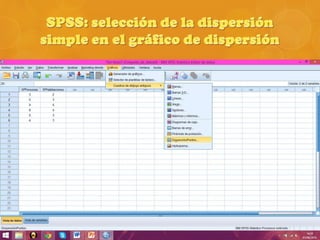
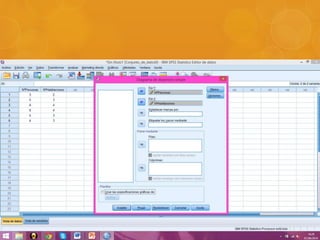
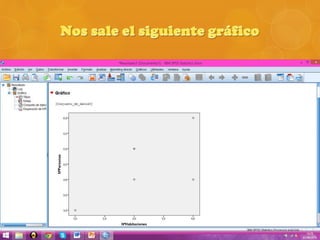
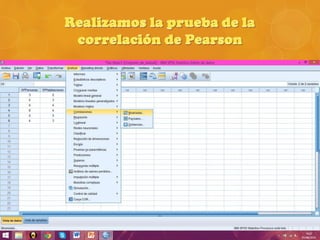
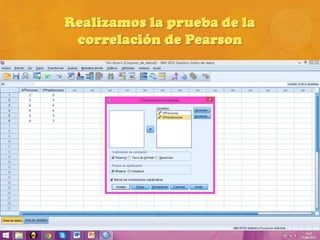
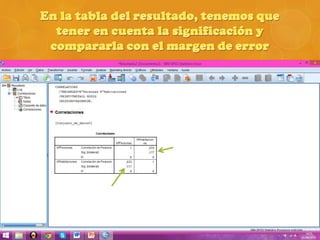
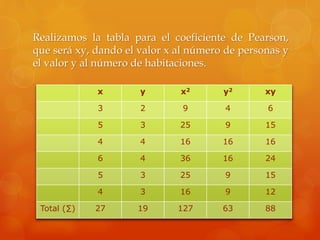
Se realizó una encuesta en un municipio español sobre el número de personas y habitaciones por hogar. Se calculó el coeficiente de correlación de Pearson entre ambas variables, el cual resultó ser 0.633, indicando una fuerte correlación. Sin embargo, al realizar la prueba t de Student, el valor obtenido fue menor que el crítico, por lo que se concluye que la correlación observada se debió al azar y no es representativa de la población.

2. En un municipio español se ha realizado una
pequeña encuesta que ha preguntado por el nº
de personas que habitan en un hogar y el nº
de habitaciones del mismo.

3. Si ambas variables se distribuyen
normalmente:
1. Averiguar si existe correlación entre ambas
variables en la población de donde derivan
los datos. Calcular el coeficiente de
correlación de Pearson.
2. Averiguar si el coeficiente de correlación es
significativo. Realizar las hipótesis.
3. Incluir los datos en SSPS y realizar gráfico
dispersión simple, realizar la correlación de
Pearson y evaluar los resultados.

4. Realizamos la tabla para el coeficiente de Pearson,
que será xy, dando el valor x al número de personas y
el valor y al número de habitaciones.
x y x2 y2 xy
3 2 9 4 6
5 3 25 9 15
4 4 16 16 16
6 4 36 16 24
5 3 25 9 15
4 3 16 9 12
Total (∑) 27 19 127 63 88

5. Con la siguiente fórmula, sustituimos por los
resultados de la tabla: (n=xy=6: coef. Pearson)
R=
6𝑥88 −(27𝑥19)
[(6𝑥127) − 272] [ 6𝑥63 − 192 ]
=
528 −513
√561
= 0’633
Como el valor de la correlación está entre 0’6 y 0’8, el
grado de correlación es fuerte (muy fuerte sería entre
0’8 y 1).

6. Realizamos la T de Student para ver si la
relación se debe al azar o la muestra es
representativa.
T = 𝑟𝑥𝑦 √[(𝑛 − 2)/(1 − 𝑟𝑥𝑦
2
)
T = 0′63 √[(6 − 2)/(1 − 0′63 2) = 1’62
Consultamos en la tabla (4 grados de
libertad): 1’62 < 2’1318: aceptamos la hipótesis
nula que dice que no hay relación (la
correlación es debida al azar y la muestra no
es representativa).

14. Al ser 1’77 mayor que 0’05 que
es el margen de error,
aceptamos la hipótesis nula, por
lo que la relación es debida al
azar, tal y como nos salió
anteriormente.