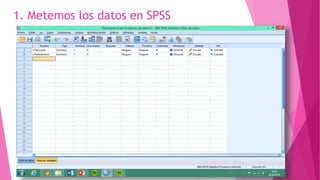
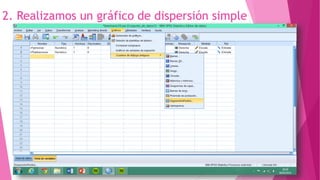
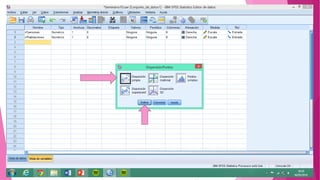
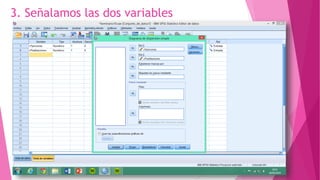
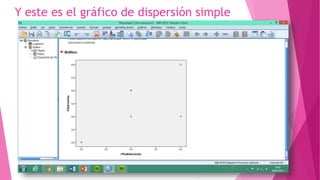
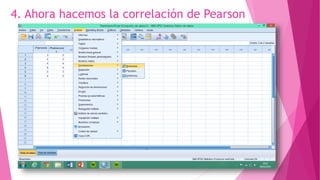
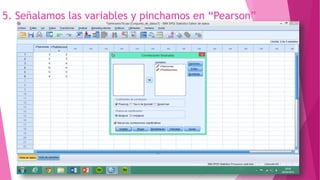
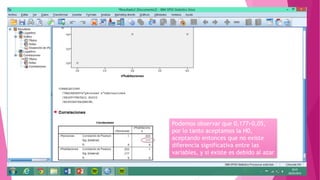
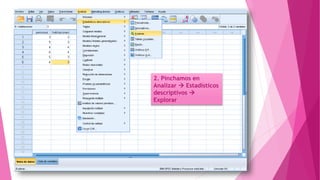
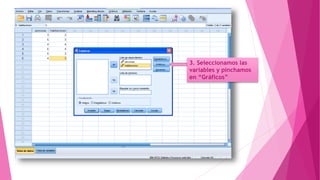
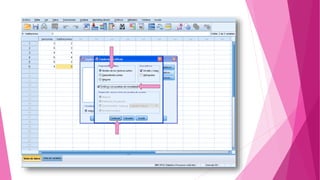
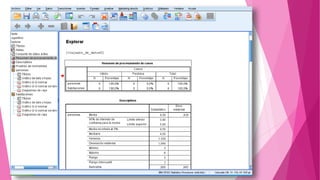
Este documento presenta un problema sobre la correlación entre el número de personas que habitan en un hogar y el número de habitaciones del mismo. Se realizó una encuesta en un municipio español y se distribuyeron normalmente ambas variables. Se calculó el coeficiente de correlación de Pearson, el cual fue significativo, indicando una correlación positiva entre las variables. Sin embargo, al aplicar la prueba t de Student, la correlación no fue estadísticamente significativa, por lo que no existe una diferencia real entre las variables.

1. SEMINARIO 10
Salud Benítez García Grupo 1

2. Problema 1
 En un municipio español se ha realizado una pequeña encuesta que ha preguntado
por el nº de personas que habitan en un hogar y el nº de habitaciones del mismo.
Si ambas variables se distribuyen normalmente:
1. Averiguar si existe correlación entre ambas variables en la población de donde
derivan los datos. Calcular el coef. De correlación de Pearson.
2. Averiguar si el coeficiente de correlación es significativo. Realizar las hipótesis.
3. Incluir los datos en SSPS y realizar gráfico dispersión simple, realizar la correlación de
Pearson y evaluar los resultados.

3.  Tenemos que comprobar si existe normalidad o no en la
muestra
- Utilizamos R Pearson si se distribuye normalmente
- Utilizamos Rho de Spearman si no se distribuye normalmente
 Para realizar las pruebas de normalidad utilizamos SPSS
o Utilizamos el test Kolmogorov- Smirnov: Si el tamaño
muestral es superior a 50
o Test de Shapiro-Wilks: Si el tamaño muestral es inferior a
50

4. Comprobamos si las variables se
distribuyen normalmente en SPSS
1. Metemos los datos
en SPSS

5. 2. Pinchamos en
Analizar  Estadísticos
descriptivos 
Explorar

6. 3. Seleccionamos las
variables y pinchamos
en “Gráficos”

9. Si el resultado de la sig. es mayor que 0,05
 se acepta la Ho, o lo que es lo mismo, se
acepta que el conjunto de datos sigue una
distribución normal
Si el resultado de la sig. es menor que 0,05
 se rechaza la Ho, o lo que es lo mismo, se
rechaza que el conjunto de datos siga una
distribución normal
Como vemos, la sig. es
mayor de 0,05  por lo
tanto aceptamos la Ho, la
muestra sigue una
distribución normal
Como la muestra es menor de 50, nos fijamos en
Shapiro-Wilks

10. Coeficiente de correlación de Pearson
 Mide la asociación entre dos variables cuantitativas
 Requiere que las variables tengan una distribución normal, por lo tanto antes
de calcularlo tenemos que comprobar si la muestra sigue una distribución
normal  como hemos hecho anteriormente.
 Mide el grado de
asociación
 Es adimensional
 Solo toma valores entre -1
y 1  a partir de 0,8 es
una correlación fuerte

11. Hacemos la fórmula
 r = coeficiente de correlacion de pearson
 Σxy= sumatorio de los productos de ambas
variables
 Σx: sumatoria de los valores de la variable
independiente
 Σy: sumatoria de los valores de la variable
dependiente
 Σx2: sumatoria de los valores al cuadrado de la
variable independiente
 Σy2= sumatoria de los valores al cuadrado de la
variable dependiente
 N: tamaño de la muestra en función de parejas
x y X2 Y2 xy
3 2 9 4 6
5 3 25 9 15
4 4 16 16 16
6 4 36 16 24
5 3 25 9 15
4 3 16 9 12
Σx=27 Σy=19 Σx2 =127 Σy2=63 Σxy=88
Nº personas X
Nº habitaciones Y N= 6

12. r=
6𝑥88 −(27𝑥19)
6𝑥127 − 729 [ 6𝑥63 − 361 ]
=0,633
Si el resultado nos da:
• O La correlación en esa
población será 0
• ≠ 0 Si existe correlación, y
hay que estudiarla mediante la
T de Student para ver si la
relación es al azar o no
Como el resultado de la correlación es 0,633≠ 0 hay que estudiarlo. Y
para eso hay que hacer la T de Student.
 Con N-2 grados de libertad, siendo N: numero de muestra
 Pearson puede ser 0 o ≠ 0 (hay una cierta relación entre variables)
 T de Student te dice si la relación se a producido al azar o no.

13.  N-2 grados de libertad, siendo N: numero de muestra gl=4
𝑇 𝑛 − 2 =
𝑟𝑥𝑦
(𝑛 − 2)
1 − 𝑟𝑥𝑦2
𝑇𝑛 − 2 = 0,633
4
1 − 0,633 2
= 1,635
Ahora vamos a comparar el valor obtenido
en T de Student con las tablas
Una vez que hemos hecho el
coeficiente de correlación de Pearson
y nos ha salido ≠ 0, vamos a ver si el
resultado es significativo mediante la
T de Student

14. Buscamos en la tabla de distribución de T de Student, para ello
vamos a suponer que tenemos un nivel de confianza del 95%,
fijándonos también que el grado de libertad es 4.
• Si T calculada > T tablas,
rechazamos hipótesis nula  por
tanto las variables están relacionadas.
• Si T calculada < T tablas, aceptamos
la hipótesis nula
por tanto no existe relación
significativa entre las variables
• Hipótesis nula (H0): No hay diferencia entre nº de
personas que habitan en un hogar y el nº de habitaciones
del mismo o que la diferencia encontrada se debe al azar
• Hipótesis alternativa (H1): Hay diferencia
estadísticamente significativa entre el nº de personas que
habitan en un hogar y el nº de habitaciones del mismo.
• La T tabla es 2,132 >1,635
que es la T calculada, por
tanto aceptamos la H0 .
Respuesta: No existe
diferencia significativa entre
el nº de personas que habitan
en un hogar y el nº de
habitaciones del mismo, y si
existe diferencia se debe al
azar.

15. En SPSS…

16. 1. Metemos los datos en SPSS

17. 2. Realizamos un gráfico de dispersión simple

19. 3. Señalamos las dos variables

20. Y este es el gráfico de dispersión simple

21. 4. Ahora hacemos la correlación de Pearson

22. 5. Señalamos las variables y pinchamos en “Pearson”

23. Podemos observar que 0,177>0,05,
por lo tanto aceptamos la H0,
aceptando entonces que no existe
diferencia significativa entre las
variables, y si existe es debido al azar