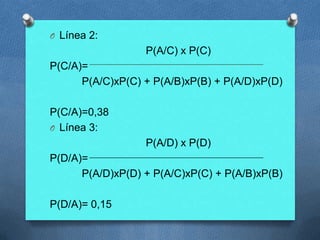
Este documento presenta cuatro problemas de probabilidad y estadística resueltos. El primer problema calcula la probabilidad de que un paciente en un hospital sea menor de 24 meses. El segundo representa gráficamente las probabilidades de dos condiciones médicas. El tercero calcula la probabilidad de averías en autobuses de diferentes líneas. El cuarto encuentra la probabilidad de acertar un blanco cuando dos personas disparan.

1. EJERCICIOS DE
ESTADÍSTICA:
SEMINARIO 7
Trabajo realizado por Inmaculada Begines
Caballero
Grupo 1 Valme, 1º Enfermeria

2. PROBLEMA 1: En la sala de pediatría de un hospital, el 60% de
los pacientes son niñas. De los niños el 35% son menores de 24
meses. El 20% de las niñas tienen menos de 24 meses. Un
pediatra que ingresa a la sala selecciona un infante al azar.
A=Niña B=Niño M=Menos de 24 meses
P(A)=0,6 P(M/A)=0,2
P(B)=0,4 P(M/B)=0,35

3. a.)Determine el valor de la probabilidad de que sea
menor de 24 meses.
Calculamos la probabilidad total que seria
P(M).
P(M)=P(M/A) x P(A) + P(M/B) x P(B)
P(M)=(0,2x0,6) + (0,35x0,4)=0,26
Solución: La probabilidad de que sea menor
de 24 meses es del 26%

4. b.) Si el infante resulta ser menor de 24 meses.
Determine la probabilidad que sea una niña.
Para ello aplicamos el teorema de Bayer.
P(M/A) x P(A)
P(A/M)=
P(M/A) x P(A) + P(M/B) x P(B)
P(A/M)=0,46
Solución: La probabilidad de que un infante
menor de 24 meses sea niña es del 46%.

5. PROBLEMA 2: Un 15% de los pacientes atendidos en la
Consulta de Enfermería del Centro de Salud de el
Cachorro padecen hipertensión arterial (A) y el 25%
hiperlipemia (B). El 5% son hipertensos e hiperlipémicos.
A=Hipertension arterial B=Hiperlipemia C=
ambas
a.) Cuál es la probabilidad de A, B y de la de
unión.
P(A)= 0,15
P(B)= 0,25
P(C)= 0,05

6. b.) Representa la situación en un diagrama de Venn
0,10
0,200,05
0,65

7. c.) Calcula la probabilidad de que una persona al
azar no padezca ni a ni b.
Probabilidad total es 0,10+0,20+0,03= 0,35
La probabilidad de que una persona no
padezca ni una ni otra seria:
1 - Ptotal= 1 - 0,35=0,65
Solución:La probabilidad de que una
persona no padezca ninguna de las dos es
65%.

8. PROBLEMA 3: Una compañía de transporte público tiene
tres líneas en una ciudad, de forma que el 45% de los
autobuses cubre el servicio de la línea 1, el 25% cubre la
línea 2 y el 30% cubre el servicio de la línea 3. Se sabe que la
probabilidad de que, diariamente, un autobús se averíe es
del 2%, 3% y 1% respectivamente, para cada línea.
B=Autobuses línea 1 P(B)=0,45
C=Autobuses línea 2 P(C)=0,25
D=Autobuses línea 3 P(D)=0,30
A=Avería
P(A/B)=0,02
P(A/C)=0,03
P(A/D)=0,01

9. a.) Calcular la probabilidad de que, en un día, un
autobús sufra una avería
Para ello calculamos la probabilidad total.
Ptotal=P(A)=P(A/B) x P(B) + P(A/C) x P(C) + P(A/D) x
P(D)
Ptotal= ((0,02x0,45) + (0,03x0,25) + (0,01x0,30)
Ptotal=P(A)=0,0195
Solución=La probabilidad de que, en un dia, un
autobús sufra una averia es del 1,95%.

10. b.) Calcular la probabilidad de que, en un día, un
autobús no sufra una avería
Para ello tendríamos que hacer 1-Ptotal
1 - Ptotal= 1 – P(A)= 1 – 0,0195
1 – Ptotal= 0,9805
Solución:La probabilida de que, en un
dia, un autobús sufra una averia es del
98,05%

11. c.) ¿De qué línea de transporte es más probable que
un autobús sufra una avería?
Para averiguarlo aplicamos el teorema de
Bayer.
O Línea 1:
P(A/B) x P(B)
P(B/A)=
P(A/B)xP(B) + P(A/C)xP(C) +
P(A/D)xP(D)
P(B/A)=0,46

12. O Línea 2:
P(A/C) x P(C)
P(C/A)=
P(A/C)xP(C) + P(A/B)xP(B) + P(A/D)xP(D)
P(C/A)=0,38
O Línea 3:
P(A/D) x P(D)
P(D/A)=
P(A/D)xP(D) + P(A/C)xP(C) + P(A/B)xP(B)
P(D/A)= 0,15

13. Solución problema 3:
Es mas probable que sufra un accidente la
línea de transporte une ya que es la que
tiene mayor riesgo de sufrirlo pues esta
tiene un 46% mientras que la 2 un 38% y la
3 un 15%.

14. PROBLEMA 4: La probabilidad de que A dé en el blanco
es 1/4 y la de B es 2/5.Si A y B disparan,
¿Cuál es la probabilidad de que pegue en el blanco?
P(A)= 0,25 P(B)=0,4
Para averiguarlo, como son sucesos
independientes utilizamos la probabilidad de
intersección.
P(A∩B)=P(A) x P(B)
P(A∩B)= 0,1
Solución: La probabilidad de que pegue en el
blanco es del 10%.