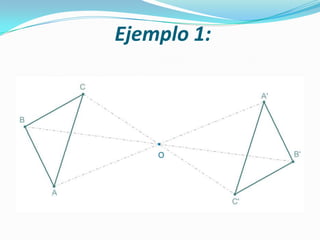
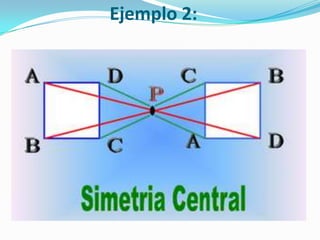
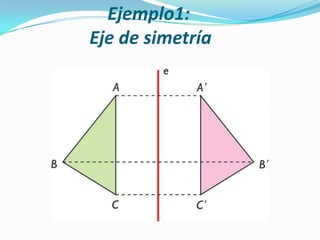
La simetría es la propiedad de un objeto cuando sus características (forma, tamaño y posición) son las mismas en ambos lados de una línea divisora o en torno a un centro. Existen dos tipos de simetría: la simetría respecto a un punto, donde los puntos están alineados con el punto central; y la simetría respecto a una recta, donde el segmento entre los puntos es perpendicular al eje de simetría y las distancias a dicho eje son iguales. El documento proporciona ejemp

1. 5.La simetríaLa Simetría es la propiedad de un objeto cuando las características (forma, tamaño y posición relativa de sus partes) son las mismas en ambos lados de una línea divisora o en torno a un centro.

2. 5.1 Simetría respecto a un punto Una simetría respecto a un punto 0 (centro de simetría), S (0), es un movimiento que asocia a cada punto P otro punto P´, tales que: Los puntos P,0 y P´ están alineados, es decir, pertenecen a una misma recta

3. El punto 0 es el punto medio del segmento PP´.Ejemplo 1:

4. Ejemplo 2:

5. Ejercicios:1- Haz la simetría central de estos dibujos. (pág 207 nº 54)2- Obtén la simetría central de esta figura.(pág 196 n. 13)

6. 5.2 Simetría respecto a una rectaUna simetría respecto a una recta r, Sr, es un movimiento que asocia a cada punto P otro punto P´, tales que:- El segmento PP´ es perpendicular a r. - Las distancias desde P y P´ a r son iguales.Por tanto, la recta r es mediatriz del segmento PP´ y se denomina eje de simetría.

7. Ejemplo1:Eje de simetría

8. Ejemplo 2:

9. Ejercicios:1- Obtén mediante el eje de simetría la siguiente figura transformada (pág 197 nº 16).2- Obtén con el eje de simetría estos dibujos.