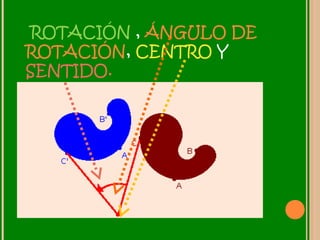
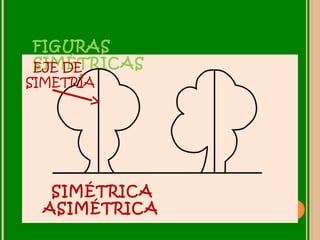
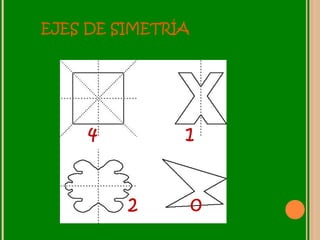
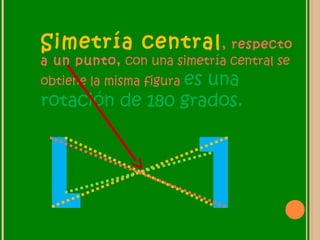
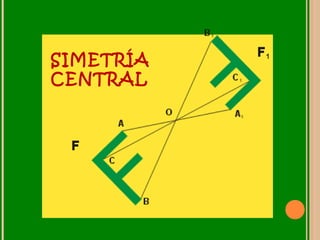
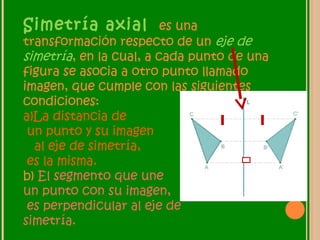
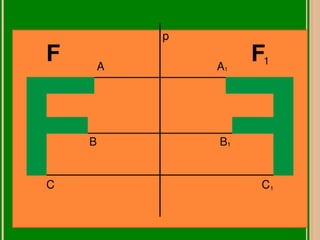
Este documento describe las transformaciones isométricas, que son transformaciones que no cambian las dimensiones ni el área de una figura. Existen tres tipos de transformaciones isométricas: la traslación, que cambia la posición de una figura; la rotación, que cambia la orientación de una figura alrededor de un punto fijo; y la simetría, que crea una figura simétrica respecto a un eje, punto o plano. El documento proporciona ejemplos e ilustraciones de cada tipo de transformación isométrica

1. TRANSFORMACIONE
S
ISOMÉTRICAS

2. TRANSFORMACIONES
ISOMÉTRICAS :
son transformaciones de figuras
en el plano que se realizan sin
variar las dimensiones ni el área
de las mismas; la figura inicial y
la final son congruentes.

3. La palabra isometría tiene su
origen en el griego iso (igual o mismo)
y metria (medir), una definición
cercana es igual medida. Existen
tres tipos de isometrías:
 traslación
 simetría
 rotación.

4. TRASLACIÓN
es una isometría que realiza
un cambio de posición ,
determinado por un vector,
con dirección
Sentido y magnitud

5. TRASLACIÓN DE UN
TRIÁNGULO

7. Una ROTACIÓN, es un
movimiento de cambio de
orientación, se deben considerar:
•Un punto denominado centro de
rotación.
•Un ángulo
•Un sentido de rotación.

8. CENTRO DE
ROTACIÓN

9. ROTACIÓN , ÁNGULO DE
ROTACIÓN, CENTRO Y
SENTIDO.

10. FIGURAS
SIMÉTRICAS
SIMÉTRICA
ASIMÉTRICA
EJE DE
SIMETRÍA

11. Simetría en
edificios y
monumentos.
Simetría en
un paisaje.

12. Eje de simetría es una línea
imaginaria que al dividir una figura
cualquiera, lo hace en dos partes, y
cuyos puntos son equidistantes a
dicho eje.
Al doblar la figura por
el eje, las partes coinciden
totalmente, luego,
son congruentes.

13. Dos ejes de SIMETRÍA

14. EJES DE SIMETRÍA
4 1
2 0

15. Simetría central, respecto
a un punto, con una simetría central se
obtiene la misma figura es una
rotación de 180 grados.

16. SIMETRÍA
CENTRAL

17. Simetría axial es una
transformación respecto de un eje de
simetría, en la cual, a cada punto de una
figura se asocia a otro punto llamado
imagen, que cumple con las siguientes
condiciones:
a)La distancia de
un punto y su imagen
al eje de simetría,
es la misma.
b) El segmento que une
un punto con su imagen,
es perpendicular al eje de
simetría.

19. SIMETRÍA AXIAL

20. EJERCICIOS

21. FIN