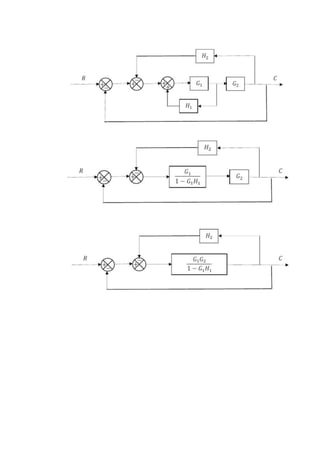
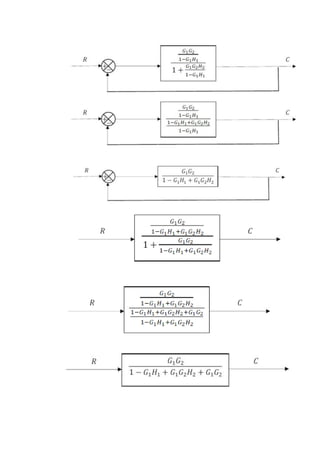
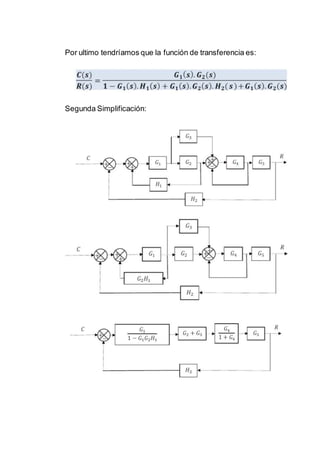
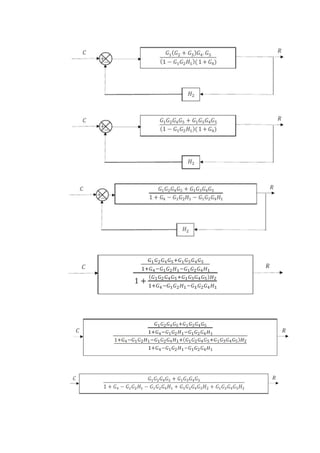
Este documento presenta tres circuitos eléctricos y sus respectivas funciones de transferencia. Se obtienen las funciones de transferencia transformando las ecuaciones de cada circuito del dominio del tiempo al dominio de Laplace. Adicionalmente, se presentan dos diagramas de bloques y sus correspondientes funciones de transferencia luego de simplificarlos.

1. REPÚBLICA BOLIVARIANA DE VENEZUELA
INSTITUTO UNIVERSITARIO POLITÉCNICO
“SANTIAGO MARIÑO”
ESCUELA DE INGENIERÍA ELECTRÓNICA
Tarea 3: Simplificación de diagrama de
bloque / función de transferencia
Asesor: Autor:
Ing. Mariangela Pollonais Grelyse Valdez
Teoría de Control C.I: 26.228.040
Maturín, febrero de 2017

2. 1. Obtenga la función de transferencia de cada uno de los
siguientes circuitos, considerandolatensiónUe(t)comoentradayla
tensión Ms(t) como salida.
Circuito Nº 1:
Para las condiciones iniciales iguala cero del circuito en el
dominio del tiempo:
𝒖 𝒆( 𝒕) = 𝑽𝑹 + 𝑽𝑪
𝒎( 𝒕) = 𝑽𝑪
Siendo Voltaje del capacitor
𝟏
𝒄
∫ 𝒊 𝒅𝒕 obtenemosque:
𝒖 𝒆( 𝒕) = 𝒊( 𝒕) 𝑹 +
𝟏
𝒄
∫ 𝒊( 𝒕) 𝒅𝒕
𝒎( 𝒕) =
𝟏
𝒄
∫ 𝒊( 𝒕) 𝒅𝒕
Llevandoestá ecuación al dominio de Laplace:
𝑼𝒆( 𝒔) = 𝒊( 𝒔) 𝑹+
𝟏
𝒔𝑪
∗ 𝒊( 𝒔) ≈ 𝒊( 𝒔) 𝑹+
𝒊( 𝒔)
𝒔𝑪
𝑼𝒆( 𝒔) = 𝒊( 𝒔)(𝑹 +
𝟏
𝒔𝑪
) ≫≫≫
𝒊( 𝒔)( 𝑹𝒔𝑪 + 𝟏)
𝒔𝑪
𝑴( 𝒔) =
𝒊( 𝒔)
𝒔𝑪
≫≫≫ 𝒊( 𝒔) = 𝒔𝑪 𝑴( 𝒔)

3. Sustituyendonos queda:
𝑼𝒆( 𝒔) =
𝒔𝑪 𝑴( 𝒔)( 𝑹𝒔𝑪 + 𝟏)
𝒔𝑪
= 𝑴( 𝒔) ( 𝑹𝒔𝑪 + 𝟏)
𝑴( 𝒔)
𝑼𝒆( 𝒔)
=
1
𝑅𝑠𝐶 + 1
Circuito Nº 2:
Para las condiciones iniciales tendremos que:
−𝑢𝑒( 𝑡) = 𝑉𝑅 + 𝑉𝐿
Recordemosque el voltaje de la bobina (VL)Está dado por L
di/dt
𝑢𝑒 = 𝑖( 𝑡) 𝑅 + 𝐿
𝑑𝑖( 𝑡)
𝑑𝑡
𝑚( 𝑡) = 𝐿
𝑑𝑖( 𝑡)
𝑑𝑡
En el dominio de la frecuencia se expresa de la siguiente
manera:
𝑈𝑒( 𝑠) = 𝐼( 𝑠) 𝑅 + 𝐼( 𝑠) 𝑆𝐿 = 𝐼𝑠(𝑅 + 𝑆𝐿)
𝑀( 𝑠) = 𝐼( 𝑠) 𝑆𝐿
𝑀( 𝑠)
𝑈𝑒( 𝑠)
=
𝑆𝐿. 𝐼𝑠
𝐼𝑠 (𝑅 + 𝑆𝐿)
=
𝑠𝐿
𝑅 + 𝑠𝐿
Circuito Nº 3:

4. Dadas las condiciones iniciales tendremos que:
𝑢𝑒( 𝑡) = 𝑉𝐿 + 𝑉𝑅 + 𝑉𝐶
𝑢𝑒( 𝑡) = 𝐿
𝑑𝑖
𝑑𝑡
+ 𝐼. 𝑅 +
1
𝐶
∫ 𝐼 ( 𝑡) 𝑑𝑡
𝑈𝑒( 𝑡) = 𝑉𝐶
𝑀( 𝑡) =
1
𝑐
∫ 𝐼 ( 𝑡) 𝑑𝑡
Aplicando la Place
𝑈𝑒( 𝑠) = 𝑆𝐿. 𝐼( 𝑠) + 𝐼( 𝑠) 𝑅 + 𝐼𝑠 .
1
𝑆𝑐
𝑀( 𝑠) = 𝐼𝑠 .
1
𝑆𝑐
𝑀( 𝑠)
𝑈𝑒(𝑠)
=
1
𝑆𝑐
∗ 𝐼(𝑠)
𝐼( 𝑠) (𝑆2 + 𝐿𝐶 + 𝑅𝑆𝐶 + 1)
𝑆𝑐
𝑀( 𝑠)
𝑈𝑒(𝑠)
=
1
𝑆2 + 𝐿𝐶 + 𝑅𝑆𝐶 + 1
2. Obtenga la función de transferencia de los siguientes sistemas
cuyos diagramas de bloques son:
Primera simplificación:

7. Por ultimo tendríamos que la función de transferencia es:
Segunda Simplificación:

9. La función de transferencia obtenida es: