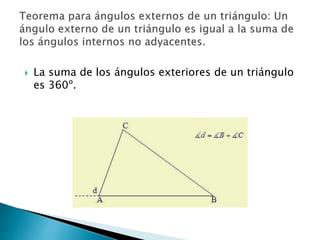
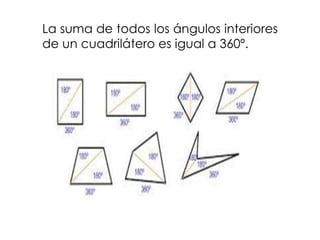
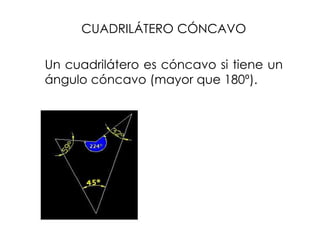
La geometría es importante enseñar en preescolar. El documento explica las sumas de ángulos en figuras geométricas como triángulos, cuadrilateros, pentágonos y hexágonos. También define polígonos por el número de lados y tipos como convexos, cóncavos y regulares.

1. Diana Alemán
Isabel Martínez
Cynthia Rodríguez
Miguel Pérez

2.  Es de suma importancia hablar sobre la
geometría en los niveles iniciales de los niños,
tal como es el Preescolar, en dónde los
educandos además de conocer las formas y los
colores de las figuras, irán aprendiendo a
mayor profundidad sobre las características de
dichas figuras. Por lo que nosotros
abordaremos el tema de los Ángulos externos y
externos de diferentes figuras geométricas
con una serie de actividades a desarrollar
aunque para ello nos remitiremos primero a la
teorías de las sumas de los ángulos.

5.  La suma de los ángulos exteriores de un triángulo
es 360º.

6. La suma de todos los ángulos interiores
de un cuadrilátero es igual a 360º.

7. CUADRILÁTERO CÓNCAVO
Un cuadrilátero es cóncavo si tiene un
ángulo cóncavo (mayor que 180º).

8. CUADRILÁTERO CONVEXO
Un cuadrilátero es convexo cuando
cada uno de sus ángulos interiores es
menor que 180º:

9. PARALELOGRAMOS
Son los cuadriláteros cuyos lados opuestos son
paralelos
A) que los lados AB y CD, son iguales, lo mismo que
AD y BC
B) Los ángulos opuestos son también iguales
C)Las diagonales se cortan en su punto medio O.

11. La palabra polígono procede del griego. En
griego, poli significa muchos y gonos significa
lados.
Los polígonos son formas bidimensionales.
Están hechos con líneas rectas, y su forma es
"cerrada" (todas las líneas están conectadas).

12. Polígono
(lados rectos)
No es un polígono
(tiene una curva)
No es un polígono
(abierto, no cerrado)

13.  Los polígonos según el número de lados que
tienen reciben nombres diferentes.
 Un polígono o figura cerrada necesita al
menos tres lados porque con menos no
puede cerrarse un área, una superficie.

14. Número de lados Nombre del polígono
3 triángulo
4 cuadrilátero
5 pentágono
6 hexágono
7 heptágono
8 octógono
9 eneágono
10 decágono
11 endecágono
12 dodecágono
13 tridecágono
14 tetradecágono
15 pentadecágono
16 hexadecágono
17 heptadecágono
18 octodecágono
19 eneadecágono
20 isodecágono
30 triacontágono
40 tetracontágono
50 pentacontágono
60 hexacontágono
70 heptacontágono
80 octacontágono
90 eneacontágono
100 hectágono

15. Simple o complejo:
 Un polígono simple sólo tiene un borde que
no se cruza con él mismo.
 ¡Uno complejo se interseca consigo mismo!

16. Polígono simple
(este es un pentágono)
Polígono complejo
(también es un pentágono)

17. Cóncavo o convexo
 Un polígono convexo no tiene ángulos que
apunten hacia dentro. En concreto, los ángulos
internos no son mayores que 180°.
 Si hay algún ángulo interno mayor que 180°
entonces es cóncavo. (Para acordarte: cóncavo
es como tener una "cueva")

18. Convexo Cóncavo

19.  Si todos los ángulos son iguales y los lados
también, es regular, si no es irregular
Regular Irregular

20.  La suma de los ángulos exteriores de un
polígono es igual a
360 grados o radianes cuando se considera
solamente un ángulo exterior por cada vértice
del polígono, sin importar el número de lados
de éste. Cuando se consideran los dos
ángulos externos posibles de cada vértice, la
suma de todos ellos es igual a 720° o rad.

22. Suma de los
ángulos interiores

23. Si es regular...
Figura Lados
Suma de los
ángulos interiores
Forma Cada ángulo
Triángulo 3 180° 60°
Quadrilátero 4 360° 90°
Pentágono 5 540° 108°
Hexágono 6 720° 120°
... ... .. ... ...
Cualquier
polígono
n (n-2) × 180° (n-2) × 180° / n
La regla general
Así que cada vez que añadimos un lado más (de triángulo a cuadrilátero, a pentágono, etc)
sumamos otros 180º total

24. Un pentágono tiene 5
lados, y se puede
dividir en tres
triángulos, así que ...
... sus ángulos
interiores suman 3 ×
180° = 540°
Y si es regular (todos
los ángulos son
iguales), cada uno
mide 540° / 5 = 108°
(Ejercicio: asegúrate
de que cada triángulo
aquí suma 180°, y
comprueba que los
ángulos interiores del
pentágono suman
540°)
Pentágono

25. Suma de los ángulos interiores = (n-2) × 180° = (10-2)×180°
= 8×180° = 1440°
Y, si es regular, cada ángulo interior = 1440°/10 = 144°
Ejemplo: ¿Qué pasa con un decágono (10 lados)?

26. ¿CUÁL ES LA SUMA DE
SUS ÁNGULOS
EXTERNOS?
330°
TRIÁNGULO

27. ¿CUÁNTO MIDEN SUS
ÁNGULOS INTERNOS Y
CUANTO SUMAN?
255°
CUADRILÁTERO

28. PENTÁGONO
¿CUÁNTO SUMAN SUS
ÁNGULOS INTERIORES Y
CUANTO VALE CADA
UNO?

29. HEXÁGONO
¿CUANTO SUMAN
SUS ÁNGULOS
INTERNOS?