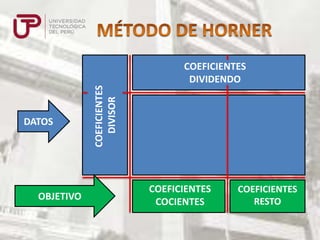
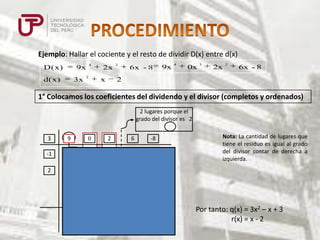
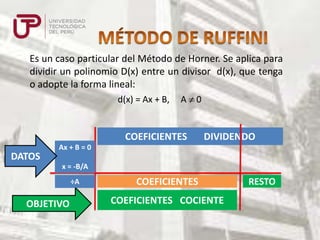
Este documento presenta diferentes métodos para dividir polinomios, incluyendo la división de monomios, polinomios entre monomios, polinomios entre polinomios usando métodos como Horner y Ruffini. También explica cómo encontrar el resto de una división sin efectuarla reemplazando la variable por su valor en el dividendo.

1. PRODUCTOS NOTABLES
DIVISIÓN ALGEBRAICA
COCIENTES NOTABLES
EQUIPO DE CIENCIAS

2. ESQUEMA DE LA UNIDAD
PRODUCTOS
NOTABLES, DIVISIÓN
ALGEBRAICA, COCIENTES
NOTABLES
PRODUCTOS
NOTABLES:
DEFINICIÓN
TABLA DE IDENTIDADES
CASOS ESPECIALES
DIVISIÓN ALGEBRAICA:
COCIENTES NOTABLES:
ELEMENTOS
CONCEPTO
CASOS
CASOS
MÉTODOS DE DIVISIÓN
TÉRMINO GENERAL
TEOREMA DEL RESTO

3. Monomio entre monomio.- Para dividir dos monomios
solo dividimos parte constante entre parte constante y
parte variable entre parte variable.
Ejemplo 1: Efectuar: 15x4y5
2x2y
Recuerda:
x
x
4
15 x y
2
2x y
5
4
15 x y
2
2
5
x y
2
7 .5 x y
4
m
n
x
m
n

4. Polinomio entre monomio.-Para dividir un polinomio
entre un monomio se divide cada término del polinomio
entre el monomio.
3
4
15 x y z
Ejemplo 1: Efectuar
2
7
25 x y
4
3
5x y z
3
4
2
7
25 x y
3
5x y z
5
18 x z
4
Recuerda que se
divide cada
término del
polinomio entre el
monomio.
3x y
3
5x y z
3
3
2
3
5x y z
18
2
2
5x z
3
2
1
3
4
5
18 x z
2
15 x y z
4
3
3
xy z
5
3
4
2
Luego, 15 x y z
7
25 x y
4
3
5x y z
2
3
5
18 x z
3
1
3x y
3
5x z
2
18
5
3
xy z

5. Polinomio entre Polinomio.- Para poder dividir un polinomio
entre polinomio. Generalmente de una variable (División
Euclidiana) se utilizan métodos prácticos como Horner, Ruffini
con la finalidad que verifique la siguiente identidad.
D ( x)
d ( x)q ( x)
Donde:
D(x):Dividendo
d(x):Divisor
q(x):Cociente
r(x):Resíduo o Resto
r ( x)
Nota:
r(x)=0 “División
Exacta”
r(x) 0 “División
Inexacta”

6. DATOS
OBJETIVO
COEFICIENTES
DIVISOR
COEFICIENTES
DIVIDENDO
COEFICIENTES
COCIENTES
COEFICIENTES
RESTO

7. Ejemplo: Hallar el cociente y el resto de dividir D(x) entre d(x)
D(x)
4
9x
d(x)
3x
2
2x
x
2
6x - 8
9x
4
0x
3
2x
2
6x - 8
2
1° Colocamos los coeficientes del dividendo y el divisor (completos y ordenados)
2 lugares porque el
grado del divisor es 2
3
9
2
-3
-1
0
6
2
1
6
-8
Nota: La cantidad de lugares que
tiene el residuo es igual al grado
del divisor contar de derecha a
izquierda.
-2
-3
6
3
-1
3
1
-2
x2
x
T.I
x
T.I
Por tanto: q(x) = 3x2 – x + 3
r(x) = x - 2

8. Es un caso particular del Método de Horner. Se aplica para
dividir un polinomio D(x) entre un divisor d(x), que tenga
o adopte la forma lineal:
d(x) = Ax + B,
A
0
COEFICIENTES
DATOS
DIVIDENDO
Ax + B = 0
x = -B/A
÷A
OBJETIVO
COEFICIENTES
COEFICIENTES COCIENTE
RESTO

9. Ejemplo: Hallar el cociente y el resto de dividir D(x) entre d(x)
8x 4
10x3 x 5
4x 3
D(x) = 8x4 + 10x3 – x + 5 = 8x4 + 10x3 + 0x2 – x + 5
d(x) = 4x - 3
1° Colocamos los coeficientes del dividendo y el divisor (completos y ordenados)
4x - 3 = 0
8
10
0
-1
5
6
12
9
6
8
16
12
8
11
2
4
3
2
x = 3/4
x
4
Por tanto: q(x) = 2x3 + 4x2 +3x + 2
r(x) = 11
Nota: La cantidad de lugares que
tiene el residuo es igual a la unidad;
es decir, igual al grado del divisor.

10. Nos permite hallar el resto de una división, sin efectuarla:
Enunciado:
En toda división de la forma
valor numérico de P(x).
Es decir:
P ( x)
Ax
B
, el residuo es igual al

11. Ejemplo:
Hallar el resto en:
Solución:
x3 3x2 3x 1
x 2
P(x) = x3 – 3x2 + 3x - 1
1° El divisor se iguala a cero
d(x) = x + 2 = 0
x = -2
2° Se elige una variable conveniente y se despeja esta variable.
En nuestro caso:
x = -2
3° La variable elegida se busca en el dividendo para reemplazarlo por su
equivalente, luego se realizan las operaciones indicadas y obtenemos el resto.
R = P(-2)
R = (-2)3 - 3(-2)2 + 3(-2) - 1
R = -8 - 12 - 6 - 1
R = -27
Recuerda:
«R» es el resto, en
consecuencia la
respuesta es -27.

13. EVALUACIÓN
1. Hallar el resto al dividir:
4x
2
2x
3
x
3x
2
2
2. Hallar el cociente de la siguiente división:
x
3
5x
x
2
2
2x
7x
5
3
PIERRE DE FERMAT