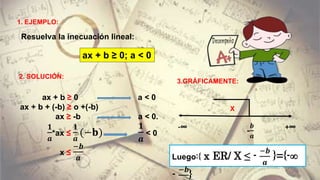
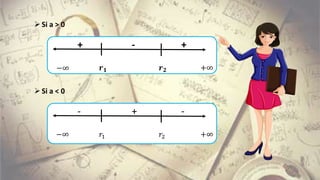
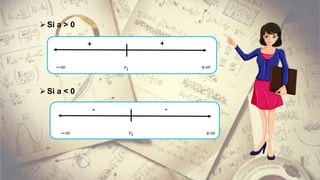
Este documento resume cómo resolver inecuaciones lineales y cuadráticas con una incógnita, aplicándolas a situaciones reales y profesionales. Explica cómo representar gráficamente las soluciones de inecuaciones lineales e identificar los intervalos de solución. También cubre conceptos como diferencia absoluta y cómo resolver inecuaciones simultáneas.

2. Resolver inecuaciones lineales con una incógnita.
Aplicar las inecuaciones lineales con una
incógnita en situaciones de contexto real y
profesional.
Resolver inecuaciones cuadráticas con una
incógnita.
Aplicar las inecuaciones cuadráticas con una
incógnita en situaciones de contexto real y
profesional.

3. En algunos casos, nos puede interesar conocer la diferencia entre los
datos recogidos y un número en particular, sin importar que esta
diferencia sea positiva o negativa.
Por ejemplo, podemos obtener la distancia de los siguientes puntos
al valor de 2:
2 3 5 90-2 x-3-5-9
Distancia: |x – 2|

4. Sean a y b constantes reales tal que a ≠ 0 y x una variable real,
llamaremos inecuación lineal a toda expresión que pueda adoptar
algunas de las siguientes formas:
ax + b < 0
ax + b > 0
ax + b ≤ 0
ax + b ≥ 0
Por ejemplo:
3x+2 > 0 es una inecuación lineal.
𝒙 𝟐
− 𝒙< 0 no es una inecuación lineal.
La solución de una inecuación lineal se puede presentar haciendo uso
intervalos en la recta numérica.

5. 1. EJEMPLO:
3.GRÁFICAMENTE:
ax + b ≥ 0 a < 0
ax + b + (-b) ≥ o +(-b)
ax ≥ -b a < 0.
𝟏
𝒂
*ax ≤
𝟏
𝒂
(−𝐛)
𝟏
𝒂
< 0
x ≤
−𝒃
𝒂
Resuelva la inecuación lineal:
X
-
𝒃
𝒂
+∞-∞
Luego:{ x ER/ X ≤ -
−𝒃
𝒂
}={-∞
-
−𝒃
}
2. SOLUCIÓN:
ax + b ≥ 0; a < 0

6. Sean a, b y c constantes reales tal que a ≠ 0 y x una variable real,
llamaremos inecuación cuadrática a toda expresión que pueda adoptar
algunas de las siguientes formas:
a𝒙 𝟐
+ bx +c < 0
a𝒙 𝟐
+ bx+ c > 0
a𝒙 𝟐
+ bx +c ≤ 0
a𝒙 𝟐
+ bx +c ≥ 0

7. Tiene ∆ = 𝒃 𝟐
- 4ac > 0, entonces la ecuación cuadrática:
E = a𝒙 𝟐
+ bx +c
Si la expresión cuadrática:
Posee dos raíces reales diferentes:
a𝒙 𝟐
+ bx +c = 0
𝒓 𝟏 y 𝒓 𝟐, con 𝒓 𝟏 < 𝒓 𝟐

8. Si a > 0
+ - +
𝒓 𝟏 𝒓 𝟐 +∞−∞
Si a < 0
- + -
𝑟1 𝑟2 +∞−∞

9. Tiene ∆ = 𝒃 𝟐 - 4ac = 0, entonces la ecuación cuadrática:
E = a𝒙 𝟐
+ bx +c
Si la expresión cuadrática:
Tiene multiplicidad de raíces, es decir:
a𝒙 𝟐
+ bx +c = 0
𝒓 𝟏 y 𝒓 𝟐, con 𝒓 𝟏 < 𝒓 𝟐

10. Si a > 0
+ +
𝑟1 +∞−∞
Si a < 0
- -
𝑟1 +∞−∞

11.  Si a > 0 y a𝒙 𝟐+ bx +c > 0 entonces CS =ℝ
 Si a > 0 y a𝒙 𝟐+ bx +c < 0 entonces CS =Ø
E= a𝒙 𝟐
+ bx +c
Si la expresión cuadrática:
Tiene ∆ = 𝒃 𝟐
- 4ac = 0, entonces la ecuación cuadrática no tiene una
sola raíz real, por lo tanto:

12. Son inecuaciones que tienen soluciones comunes.
¿Para qué valores de x se verifican simultáneamente las inecuaciones
10x-15 < 0 y 5x > 3?
Resolviendo las inecuaciones, la primera se cumple para x < 3/2, y la
segunda, para x >(3/5); por consiguiente, los valores mayores que 3/5
y menores que 3/2, verifican simultáneamente ambas inecuaciones.
Este resultado se escribe así: 3/5 < x < 3/2
EJEMPLO:

13. Las inecuaciones sin dudas te permitirá resolver
ejercicios no solo de la Matemática, además es de
gran importancia para la resolución de problemas
prácticos ya que son utilizados en diversas áreas.
Es importante saber que siempre trabajamos con la
inecuación en la forma general, es decir,
un polinomio desigualado a cero.

14.  http://www.uv.es/lonjedo/esoProblemas/unidad4in
ecuaciones.pdf
 http://www.fra.utn.edu.ar/catedras/sunmat/Lec_Int_
Inecuaciones.pdf
 Llanos Marcos, (2007), “Nuevo Formulario de ciencias”,
Lima – Perú: Editorial San Marcos
Visto en: