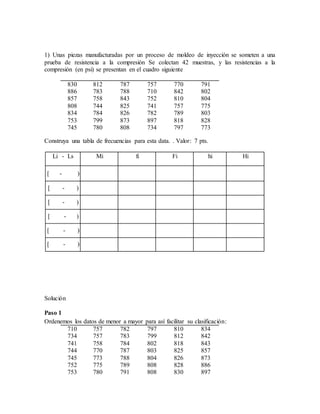
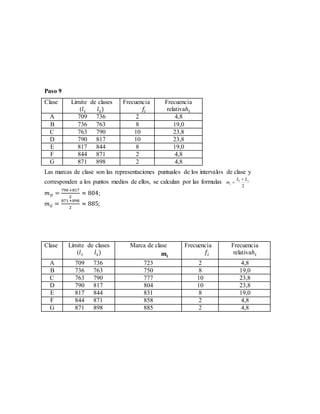
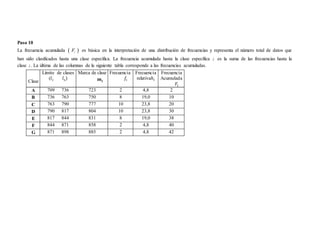
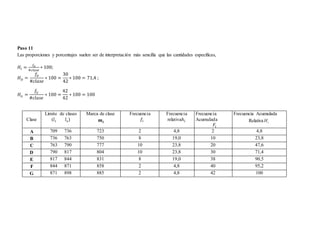
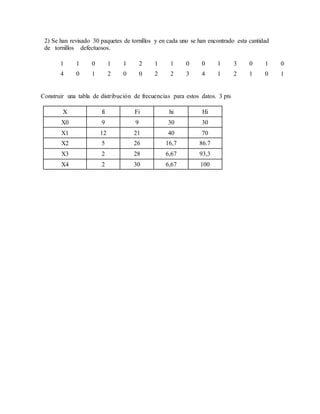
El documento detalla un procedimiento para realizar una tabla de frecuencias a partir de datos de resistencias a la compresión de piezas manufacturadas y la cantidad de tornillos defectuosos en paquetes. Se presentan pasos específicos desde la organización de datos hasta el cálculo de frecuencias acumuladas y relativas. La información incluye el rango, número de clases, límites de intervalos, y clasificación de datos.

1. República Bolivariana de Venezuela
Ministerio del Poder Popular Para La Educación
Vicerrectorado Académico Universidad Fermín Toro
Escuela De Ingeniería Eléctrica
Extensión Cabudare
Estudiante
Pedro Mendoza
C.I:27883589
Seccion: A

2. 1) Unas piezas manufacturadas por un proceso de moldeo de inyección se someten a una
prueba de resistencia a la compresión Se colectan 42 muestras, y las resistencias a la
compresión (en psi) se presentan en el cuadro siguiente
830 812 787 757 770 791
886 783 788 710 842 802
857 758 843 752 810 804
808 744 825 741 757 775
834 784 826 782 789 803
753 799 873 897 818 828
745 780 808 734 797 773
Construya una tabla de frecuencias para esta data. . Valor: 7 pts.
Li - Ls Mi fi Fi hi Hi
[ - )
[ - )
[ - )
[ - )
[ - )
[ - )
Solución
Paso 1
Ordenemos los datos de menor a mayor para así facilitar su clasificación:
710 757 782 797 810 834
734 757 783 799 812 842
741 758 784 802 818 843
744 770 787 803 825 857
745 773 788 804 826 873
752 775 789 808 828 886
753 780 791 808 830 897

3. Paso 2
Calculemos el recorrido o rango  R de los datos, es decir, la extensión del intervalo  I
que los contiene
 897,710I , el rango es 187710897  mínmáx xxR .
Paso 3
Utilicemos la “regla de la raíz” para determinar el número de clases:
742#  nClases .
Denominemos las clases como:
A, B , C , D , E , FyG,
Paso 4
El siguiente paso consiste en determinar la amplitud o ancho de cada clase A , es
conveniente que su tamaño sea un número entero, luego es necesario redondear el cociente
#
R
A
Clases
 , al número entero próximo mayor que el resultado obtenido, así
27
7
187
A
Paso 5
El paso anterior altera el tamaño del recorrido o rango  R , por tanto debemos ajustar los
límites del intervalo I que contiene a los datos, esto se obtiene como sigue. Determinemos
el nuevo recorrido (rango) NR , para ello multipliquemos el número de categorías por el
tamaño de la categoría; es decir
𝑁𝑅 = (#𝑐𝑙𝑎𝑠𝑒𝑠) ∗ ( 𝐴) = 7 ∗ 27 = 189
Paso 6
La holgura  H
𝐻 = 𝑁𝑅 − 𝑅 = 189 − 187 = 2.
Esta holgura conviene distribuirla de la manera “entera” y equitativa entre los extremos del
intervalo. Esto se logra estableciendo el Límite inferior del 1er intervalo (𝑙 𝑖) por la siguiente
fórmula
𝑙 𝑖 = 𝑥 𝑚𝑖𝑛 −
𝐻
2
= 710 −
2
2
= 709

4. Paso 7
A 𝐿 𝑖 = 709 le sumamos el ancho o amplitud de clase calculado así obtenemos el límite
superior de la primera clase L1).
𝑙 𝑠 = 𝑙 𝑖 + 𝐴
𝑙 𝑠 = 709 + 27 = 736
para obtener la frecuencia de los intervalos tomaremos el criterio siguiente:
(𝑙 𝑖 − 𝑙 𝑠) a este intervalo pertenecen todas las observaciones que son estrictamente mayores o
iguales que el valor del 𝑙 𝑖; y estrictamente menores que el 𝑙 𝑠
Ahora clasificamos los datos en los intervalos de clase, obtenemos:
Paso 8
Corresponde ahora obtener las frecuencias relativas
Formula de frecuencia relativa seria ℎ𝑖 =
𝑓𝑖
#𝑐𝑙𝑎𝑠𝑒
∗ 100
ℎ 𝐷 =
10
42
∗ 100 = 23,8 ;
ℎ 𝐺 =
2
42
∗ 100 = 4,8
Clase (𝑙 𝑖 𝑙 𝑠) 𝑓𝑖
A 709 736 2
B 736 763 8
C 763 790 10
D 790 817 10
E 817 844 8
F 844 871 2
G 871 898 2

5. Paso 9
Las marcas de clase son las representaciones puntuales de los intervalos de clase y
corresponden a los puntos medios de ellos, se calculan por las formulas
2
si
i
LL
m


𝑚 𝐷 =
790+817
2
≈ 804;
𝑚 𝐺 =
871+898
2
≈ 885;
Clase Límite de clases
(𝑙 𝑖 𝑙 𝑠)
Frecuencia
𝑓𝑖
Frecuencia
relativaℎ𝑖
A 709 736 2 4,8
B 736 763 8 19,0
C 763 790 10 23,8
D 790 817 10 23,8
E 817 844 8 19,0
F 844 871 2 4,8
G 871 898 2 4,8
Clase Límite de clases
(𝑙 𝑖 𝑙 𝑠)
Marca de clase
𝒎𝒊
Frecuencia
𝑓𝑖
Frecuencia
relativaℎ𝑖
A 709 736 723 2 4,8
B 736 763 750 8 19,0
C 763 790 777 10 23,8
D 790 817 804 10 23,8
E 817 844 831 8 19,0
F 844 871 858 2 4,8
G 871 898 885 2 4,8

6. Paso 10
La frecuencia acumulada  iF es básica en la interpretación de una distribución de frecuencias y representa el número total de datos que
han sido clasificados hasta una clase específica. La frecuencia acumulada hasta la clase específica i es la suma de las frecuencias hasta la
clase i . La última de las columnas de la siguiente tabla corresponde a las frecuencias acumuladas.
Clase
Límite de clases
(𝑙 𝑖 𝑙 𝑠)
Marca de clase
𝒎𝒊
Frecuencia
𝑓𝑖
Frecuencia
relativaℎ𝑖
Frecuencia
Acumulada
𝐹𝑖
A 709 736 723 2 4,8 2
B 736 763 750 8 19,0 10
C 763 790 777 10 23,8 20
D 790 817 804 10 23,8 30
E 817 844 831 8 19,0 38
F 844 871 858 2 4,8 40
G 871 898 885 2 4,8 42

7. Paso 11
Las proporciones y porcentajes suelen ser de interpretación más sencilla que las cantidades específicas,
𝐻𝑖 =
𝑓𝑎
#𝑐𝑙𝑎𝑠𝑒
∗ 100;
𝐻 𝐷 =
𝑓𝐷
#𝑐𝑙𝑎𝑠𝑒
∗ 100 =
30
42
∗ 100 = 71,4 ;
𝐻 𝐺 =
𝑓𝐺
#𝑐𝑙𝑎𝑠𝑒
∗ 100 =
42
42
∗ 100 = 100
Clase
Límite de clases
(𝑙 𝑖 𝑙 𝑠)
Marca de clase
𝒎𝒊
Frecuencia
𝑓𝑖
Frecuencia
relativaℎ𝑖
Frecuencia
Acumulada
𝐹𝑖
Frecuencia Acumulada
Relativa iH
A 709 736 723 2 4,8 2 4,8
B 736 763 750 8 19,0 10 23,8
C 763 790 777 10 23,8 20 47,6
D 790 817 804 10 23,8 30 71,4
E 817 844 831 8 19,0 38 90,5
F 844 871 858 2 4,8 40 95,2
G 871 898 885 2 4,8 42 100

8. 2) Se han revisado 30 paquetes de tornillos y en cada uno se han encontrado esta cantidad
de tornillos defectuosos.
1 1 0 1 1 2 1 1 0 0 1 3 0 1 0
4 0 1 2 0 0 2 2 3 4 1 2 1 0 1
Construir una tabla de distribución de frecuencias para estos datos. 3 pts
X fi Fi hi Hi
X0 9 9 30 30
X1 12 21 40 70
X2 5 26 16,7 86.7
X3 2 28 6,67 93,3
X4 2 30 6,67 100