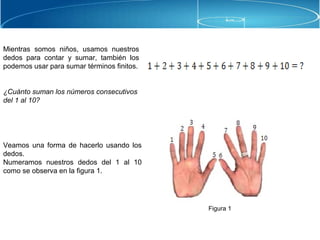
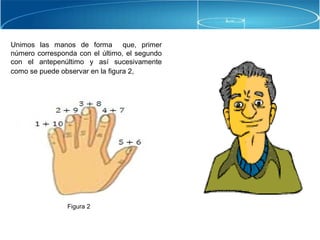
El documento discute las dificultades en el proceso de enseñanza y aprendizaje de las matemáticas. Propone utilizar un enfoque constructivista donde los estudiantes construyen conceptos a través de situaciones vivenciales. También destaca la importancia de conocer las necesidades de los estudiantes para favorecer el aprendizaje de objetos matemáticos.