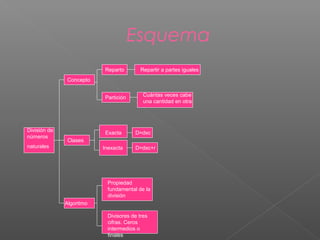
Este documento presenta los conceptos básicos de la división de números naturales. Explica la diferencia entre división exacta e inexacta y la propiedad fundamental de que el cociente no cambia cuando el dividendo y divisor se multiplican o dividen por el mismo número. También cubre cómo dividir números de tres cifras y números con ceros intermedios o finales en el cociente, así como enlaces a juegos y videos sobre división.

1. División de números
naturales
Manuel
Delgado
López
5º Curso
2013/2014

2. Indice






Esquema
División exacta y división inexacta
Propiedad fundamental de la división
La división con divisores de tres cifras
Práctica de la división
Juegos y vídeos

3. Esquema
Reparto
Repartir a partes iguales
Concepto
Partición
División de
números
Exacta
Cuántas veces cabe
una cantidad en otra
D=dxc
Clases
naturales
Inexacta
D=dxc+r
Propiedad
fundamental de la
división
Algoritmo
Divisores de tres
cifras. Ceros
intermedios o
finales

4. División exacta y división
inexacta
Repartimos en
partes iguales
Dividir es repartir en partes iguales o
averiguar cuántas veces cabe una
Cantidad en otra.
División exacta
Repartimos 84 bollos en 6 cestas.
84 6
24 14
0
Ponemos 14 bollos en cada cesta y no
sobra ninguno.
84=14x6
En una división exacta:
El resto es siempre cero (r=0)
El dividendo es igual al divisor el cociente.
D=dxc
División inexacta
Colocamos 93 bollos en cestas de 8 bollos cada una.
93 8
Llenamos 11 cestas y sobran cinco
bollos.
93=8x11+5
En una división inexacta:
El resto es siempre distinto de cero y
menor que el divisor (r=0 y r<d)
El dividendo es igual al diviso por
el cociente más el resto.
13 11
5
Ten en cuenta
252 4
12
63
0
4x63=252
dxc=D

5. Ten en cuenta
Una división inexacta está bien hecha cuando al multiplicar el divisor
por el cociente y sumarle el resto. El resultado es el dividendo.
385 24
145 16
01
24x6+1=385
dxc+r=D

6. Propiedad fundamental de la
división
Obtenemos el mismo resultado
Repartimos 40 rosquillas en bolsas
De 5 rosquillas cada una
En una división exacta, si multiplicamos o dividimos el dividendo y
el
divisor por un mismo número, el cociente no varía.
40 : 5=8
x2 x2
80 : 10=8
Si la división es inexacta, el resto queda multiplicado o dividido
por ese
Mismo número.
120 13
03
9
480 52
52

7. Propiedad fundamental de la
división
Obtenemos el mismo cociente
Repartimos 80 rosquillas en bolsas de
10 roquillas cada una.
En una división exacta, si multiplicamos
o dividimos el dividendo y el divisor
por un mismo número, el cociente
no varía.
80:10=8
:2 :2
40 : 5=8
Si la división es inexacta, el resto
queda multiplicado o dividido por
ese mismo nuemero
Recuerda
Para dividir un número terminado en
ceros entre 10, 100 ó 1000, no es
necesario realizar la división.
Basta con tachar uno dos o tres
ceros del número, respectivamente.
Así:
450:10=45
36000:100=360
4000:1000=4

8. Recuerda
Aprende
Si multiplicamos o dividimos el dividendo por un número, el cociente
queda multiplicado o dividido por ese número
21:7=3
105:7=15
x5 x5
:5
:5
105:7=15
21:7=3
Si multiplicamos (o dividimos) el divisor por un número, el cociente
queda dividido (o multiplicado) por ese número.
160:5=32
160:20=8
x4 x4
:4 x4
160:20=8
160:5=32

9. La división con divisores de tres
cifras
Dividimos entre números de
tres cifras.
C
M
DM UM
Observa la división 148590 entre 234.
1
4
0
1.º Como no podemos repartir 148UM
Entre 234, repartimos 1485C.
Tocan a 6 y sobran 81C.
81C=810D
2.º 810D+9D=819D
Repartimos 819 D entre 234.
Tocan a 3 D y sobran 117 D
117D=1170U
3.º 11708+0U=1170U
Repartimos 1170U entre 234.
Tocan a 5 D y no sobra nada.
8
8
1
C
5
1
1
0
D
9
9
7
Prueba
234
X635
1170
702
+1404
148590
U
0
234
D
6
0
C
3
U
5

10. Ten en cuenta
Utiliza el tanteo si es necesario.
18285 345
1035 53
000
345x1=345
354x2=690
345x3=1035
345x4=1380
345x5=1725

11. Práctica de la división
Ceros intermedios o
finales en el cociente
Observa cómo dividimos
382215 entre 364.
1.º Repartimos 382UM entre 364.
CM
DM
UM
C
D
U
3
0
8
1
2
8
0
2
2
0
1
1
1
5
Tocan al 1 UM y sobran 18UM.
18UM=180C.
2.º 180C+2C=182C.
No podemos repartir 182C entre 234.
Ponemos un cero en las centenas del
cociente y seguimos dividiendo.
182C=1820D
1820D+1D=1821D
Repartimos 1821D entre 364.
Tocan a 5D y sobra 1D
1D=10U
3.º 10U+5U=15U entre 364.
No podemos repartir 15U entre 364.
364
UM
Prueba
1050
X365
4200
6300
+3150
382200
+
15
382215
D
U
1
5
C
0
5
0

12. Ten en cuenta
Observa
1.º 69UM repartidas entre 23 tocan a 3UM y no sobra nada.
69920 23
00
3
2.º Bajamos el 9.
9 centenas no se pueden repartir entre 23, ponemos el cero en el cociente y seguimos.
69920 23
009 30
3.º Bajamos el 2.
92 D entre 23, tocan a 4 D y no sobra nada.
69920 23
0093 304
4.º Bajamos el 0 de las unidades.
Ponemos el cero en las unidades del cociente y terminamos la división.
69920 23
0092 3040
000

13. Juegos y vídeos

Juegos:
http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/QUINTO
/datos/03_Mates/datos/05_rdi/ud03/unidad03.htm

Vídeos: http://www.youtube.com/watch?v=wfTFrwGHUBo