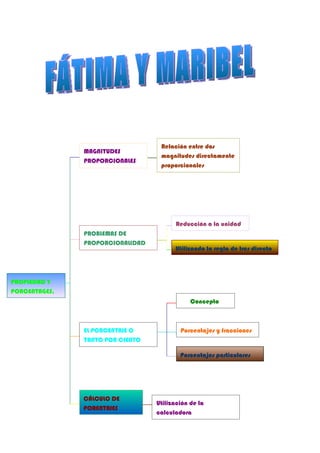
El documento describe las magnitudes directamente proporcionales y cómo resolver problemas de proporcionalidad utilizando la regla de tres. Explica que dos magnitudes son directamente proporcionales cuando una aumenta o disminuye al mismo ritmo que la otra, y proporciona ejemplos como el precio de un producto y su peso. Además, detalla cómo calcular un valor desconocido usando una tabla de proporcionalidad y la regla de tres.

1. Relación entre dos
MAGNITUDES
magnitudes directamente
PROPORCIONALES
proporcionales
Reducción a la unidad
PROBLEMAS DE
PROPORCIONALIDAD
Utilizando la regla de tres directa
PROPIEDAD Y
PORCENTAGES.
Concepto
EL PORCENTAJE O Porcentajes y fracciones
TANTO POR CIENTO
Porcentajes particulares
CÁLCULO DE
Utilización de la
PORENTAJES
calculadora

2. Dos magnitudes son directamente proporcionales cuando,
al multiplicar o dividir una de ellas por un número cualquiera, la otra
queda multiplicada o dividida por el mismo número.
Se establece una relación de proporcionalidad directa entre dos
magnitudes cuando:
A más corresponde más.
A menos corresponde menos .
Son magnitudes directamente proporcionales, el peso de un producto y
su precio.
Si 1 kg de tomates cuesta 1 €, 2 kg costarán 2 € y ½ kg costará 50
céntimos.
Es decir:
A más kilógramos de tomate más euros.
A menos kilógramos de tomate menos euros.
También son directamente proporcionales :
El espacio recorrido por un móvil y el tiempo empleado.
El volumen de un cuerpo y su peso.
La longitud de los lados de un polígono y su área.

3. En 50 litros de agua de mar hay 1300 gramos de sal. ¿Cuántos litros de agua de mar
contendrán 5200 gramos de sal?
Como en doble cantidad de agua de mar habrá doble cantidad de sal; en triple, triple,
etc. Las magnitudes cantidad de agua y cantidad de sal son directamente
proporcionales.
Si representamos por x el número de litros que contendrá 5200 gramos de sal, y
formamos la siguiente tabla:
Litros de agua 50 x
Gramos de sal 1300 5200
Se verifica la proporción:
Y como en toda proporción el producto de medios es igual al producto de extremos,
resulta:
50.5200=1300.x
Es decir
En la práctica esto se suele disponer del siguiente modo:
Esta forma de plantear y resolver problemas sobre proporciones se conoce con el
nombre deregla de tres simple directa.
En muchos problemas de la vida real intervienen dos magnitudes directamente
proporcionales. Conociendo tres cantidades nos piden calcular un cuarto dato.
Para resolverlos disponemos de dos métodos, el primero es el método de reducción
a la unidad, en el que hay que dar los siguientes pasos:
•Comprobar que las dos magnitudes son directamente proporcionales.
•Localizar el dato.
•Dividiendo se calcula el valor de la 2º magnitud que corresponde a una unidad de
la 1ª.
•Multiplicando adecuadamente se calcula el valor deseado.

4. Sigue los siguientes pasos para convertir una fracción a un porcentaje.
Por ejemplo: Convierte 4/5 a un porcentaje.
•Divide el numerador de la fracción por el denominador ( ej. 4 ÷ 5 = 0.80)
•Multiplica por 100 (Mueve el punto decimal dos lugares hacia la derecha) (ej.
0.80*100=80)
•Redondea el resultado a la precisión deseada.
•Termina tu respuesta con el signo % (ej. 80%)
Las fracciones con denominador igual a 100 se llaman fracciones porcentajes
o, simplemente, porcentajes.
Leemos: 30 por ciento; 28 por ciento; 70 por ciento; y 12 por ciento.
Podemos representar gráficamente estos porcentajes igual que se hace con las
fracciones