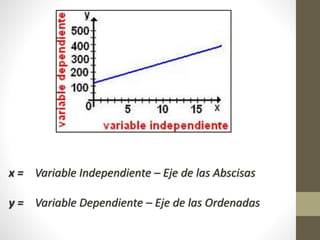
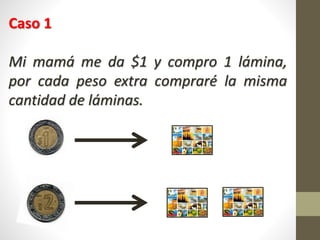
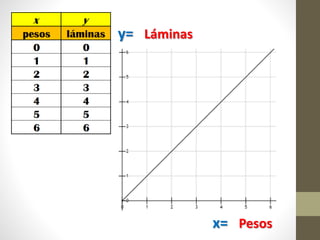
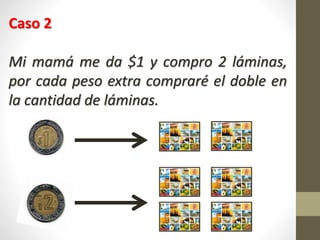
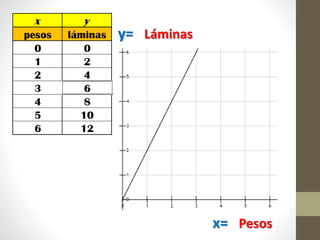
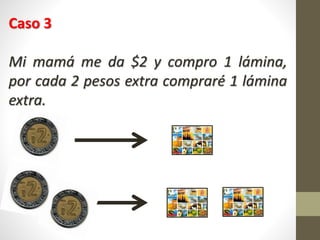
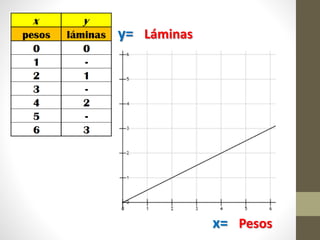
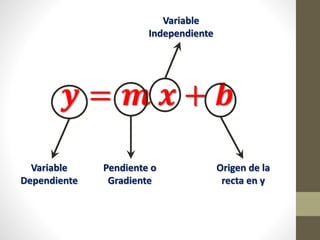
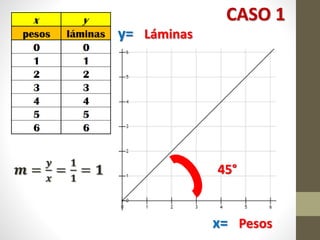
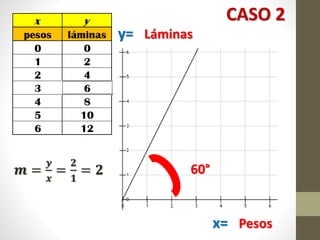
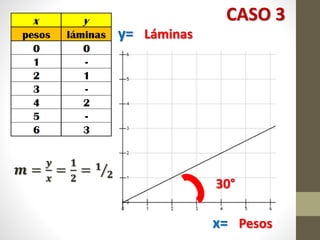
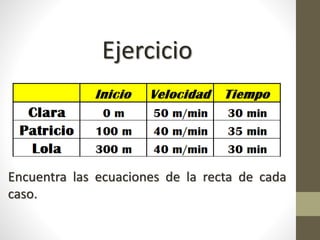
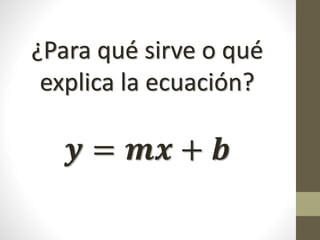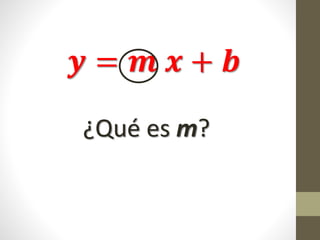Este documento explica la relación entre variables dependientes e independientes a través de ecuaciones lineales. Presenta tres casos de relaciones lineales y deriva la ecuación para cada caso. También muestra cómo calcular la pendiente m y el término b para describir completamente cada relación lineal a través de la ecuación y = mx + b.

1. Variación conjunta
entre variables
José Alejandro Sánchez Lozano

2. Recordando conceptos

3. Donde:
x = Variable Independiente
y = Variable Dependiente
k = Una constate de proporcionalidad

4. x = Variable Independiente – Eje de las Abscisas
y = Variable Dependiente – Eje de las Ordenadas

5. Ecuación de la Recta
𝒚 = 𝒎𝒙 + 𝒃

6. Caso 1
Mi mamá me da $1 y compro 1 lámina,
por cada peso extra compraré la misma
cantidad de láminas.

7. y= Láminas
x= Pesos

8. Caso 2
Mi mamá me da $1 y compro 2 láminas,
por cada peso extra compraré el doble en
la cantidad de láminas.

9. y= Láminas
x= Pesos

10. Caso 3
Mi mamá me da $2 y compro 1 lámina,
por cada 2 pesos extra compraré 1 lámina
extra.

11. y= Láminas
x= Pesos

12. ¿Para qué sirve o qué
explica la ecuación?
𝒚 = 𝒎𝒙 + 𝒃

13. 𝒚 = 𝒎 𝒙 + 𝒃
Variable
Dependiente
Variable
Independiente
Pendiente o
Gradiente
Origen de la
recta en y

14. 𝒚 = 𝒎𝒙 + 𝒃
La ecuación y = mx + b, nos explica el
comportamiento de una recta, además nos
ayuda a encontrar el valor de la variable
dependiente dándole valores a la variable
independiente en la gráfica

15. 𝒚 = 𝒎 𝒙 + 𝒃
¿Qué es m?

16. 𝒚 = 𝒎𝒙 + 𝒃
La variable m, se le conoce como pendiente o
gradiente, y nos explica la inclinación que tiene
la recta; es gradiente por la medida en grados.

17. y= Láminas
x= Pesos
CASO 1
𝒎 =
𝒚
𝒙
=
𝟏
𝟏
= 𝟏 45°

18. y= Láminas
x= Pesos
CASO 2
𝒎 =
𝒚
𝒙
=
𝟐
𝟏
= 𝟐 60°

19. y= Láminas
x= Pesos
CASO 3
𝒎 =
𝒚
𝒙
=
𝟏
𝟐
= 𝟏
𝟐
30°

20. Podemos concluir que tenemos tres casos con
respecto a la pendiente:
I. 𝒎 = 𝟏 o 𝒎 = 𝟒𝟓°:
En este caso la variación de la variable
independiente afecta en la misma proporción
a la variable dependiente
𝒚
𝒙
=
𝒅𝒆𝒑𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆
𝒊𝒏𝒅𝒆𝒑𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆
=
𝟏
𝟏

21. II. 𝒎 → 𝒎𝒂𝒚𝒐𝒓 𝒒𝒖𝒆 𝟏 o 𝒎 →
𝒎𝒂𝒚𝒐𝒓 𝒒𝒖𝒆 𝟒𝟓°:
En este caso la variación de la variable
independiente afecta en mayor proporción a
la variable dependiente
𝒚
𝒙
=
𝒅𝒆𝒑𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆
𝒊𝒏𝒅𝒆𝒑𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆
=
𝟐
𝟏

22. III. 𝒎 → 𝒎𝒆𝒏𝒐𝒓 𝒒𝒖𝒆 𝟏 o 𝒎 →
𝒎𝒆𝒏𝒐𝒓 𝒒𝒖𝒆 𝟒𝟓°:
En este caso la variación de la variable
independiente afecta en menor proporción a
la variable dependiente
𝒚
𝒙
=
𝒅𝒆𝒑𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆
𝒊𝒏𝒅𝒆𝒑𝒆𝒏𝒅𝒊𝒆𝒏𝒕𝒆
=
𝟏
𝟐

23. Ejercicio
Encuentra las ecuaciones de la recta de cada
caso.

24. CLARA
Tomamos como base la ecuación: y = mx + b
y – Queda de la misma forma
m – Pendiente: 𝑚 =
𝑦
𝑥
=
𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
=
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎
𝑡𝑖𝑒𝑚𝑝𝑜𝑠
=
𝑚𝑒𝑡𝑟𝑜𝑠
𝑚𝑖𝑛𝑢𝑡𝑜𝑠
=
𝟓𝟎
𝟏
= 50

25. x – Queda de la misma forma
b – Punto del cual se parte cuando x = 0 → 0m
Para Clara tenemos:
𝑦 = 50𝑥 + 0 → 𝑦 = 50𝑥

26. PATRICIO
Tomamos como base la ecuación: y = mx + b
y – Queda de la misma forma
m – Pendiente: 𝑚 =
𝑦
𝑥
=
𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
=
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎
𝑡𝑖𝑒𝑚𝑝𝑜𝑠
=
𝑚𝑒𝑡𝑟𝑜𝑠
𝑚𝑖𝑛𝑢𝑡𝑜𝑠
=
𝟒𝟎
𝟏
= 40

27. x – Queda de la misma forma
b – Punto del cual se parte cuando x = 0 →
100m
Para Patricio tenemos:
𝑦 = 40𝑥 + 100

28. LOLA
Tomamos como base la ecuación: y = mx + b
y – Queda de la misma forma
m – Pendiente: 𝑚 =
𝑦
𝑥
=
𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
𝑖𝑛𝑑𝑒𝑝𝑒𝑛𝑑𝑖𝑒𝑛𝑡𝑒
=
𝑑𝑖𝑠𝑡𝑎𝑛𝑐𝑖𝑎
𝑡𝑖𝑒𝑚𝑝𝑜𝑠
=
𝑚𝑒𝑡𝑟𝑜𝑠
𝑚𝑖𝑛𝑢𝑡𝑜𝑠
=
𝟒𝟎
𝟏
= 40

29. x – Queda de la misma forma
b – Punto del cual se parte cuando x = 0 →
300m
Para Lola tenemos:
𝑦 = 40𝑥 + 300

30. Para Lola tenemos:
𝒚 = 𝟒𝟎𝒙 + 𝟑𝟎𝟎
Si queremos saber cuánto ha recorrido en 10
minutos, sólo le damos vamos el valor de 10 a 𝑥
y encontramos cuánto vale 𝑦.
𝒚 = 𝟒𝟎 𝟏𝟎 + 𝟑𝟎𝟎 = 𝟒𝟎𝟎 + 𝟑𝟎𝟎 = 𝟕𝟎𝟎 𝒎𝒕𝒔
En 10 minutos, Lola ha recorrido 700 metros

31. Tarea
Tomando como base las ecuaciones de Clara,
Patricio y Lola, encuentra cuando habrá
recorrido cada uno, si corren por 40, 50, 100 y
200 minutos, construye una tabla para observar
los resultados.