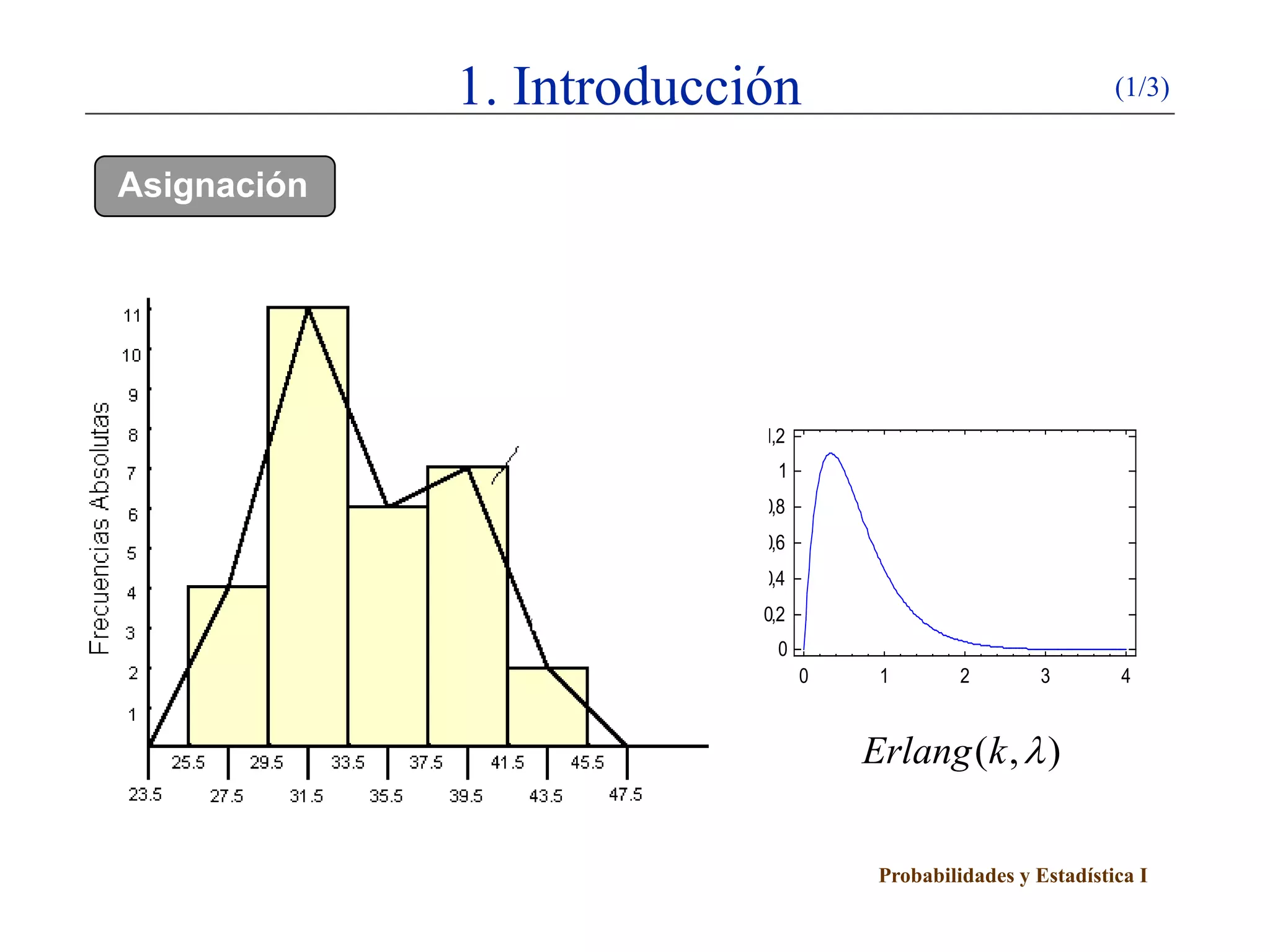
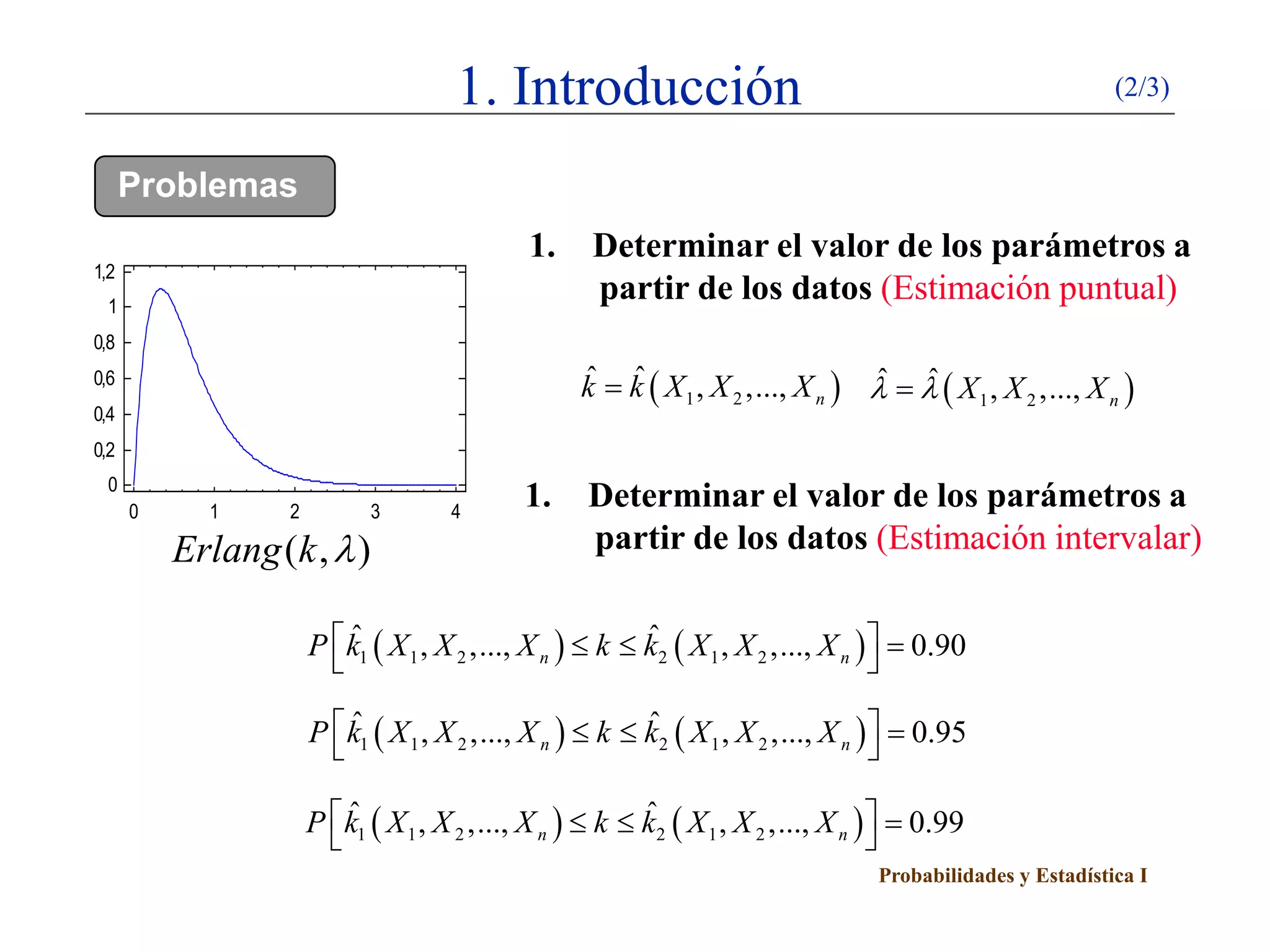
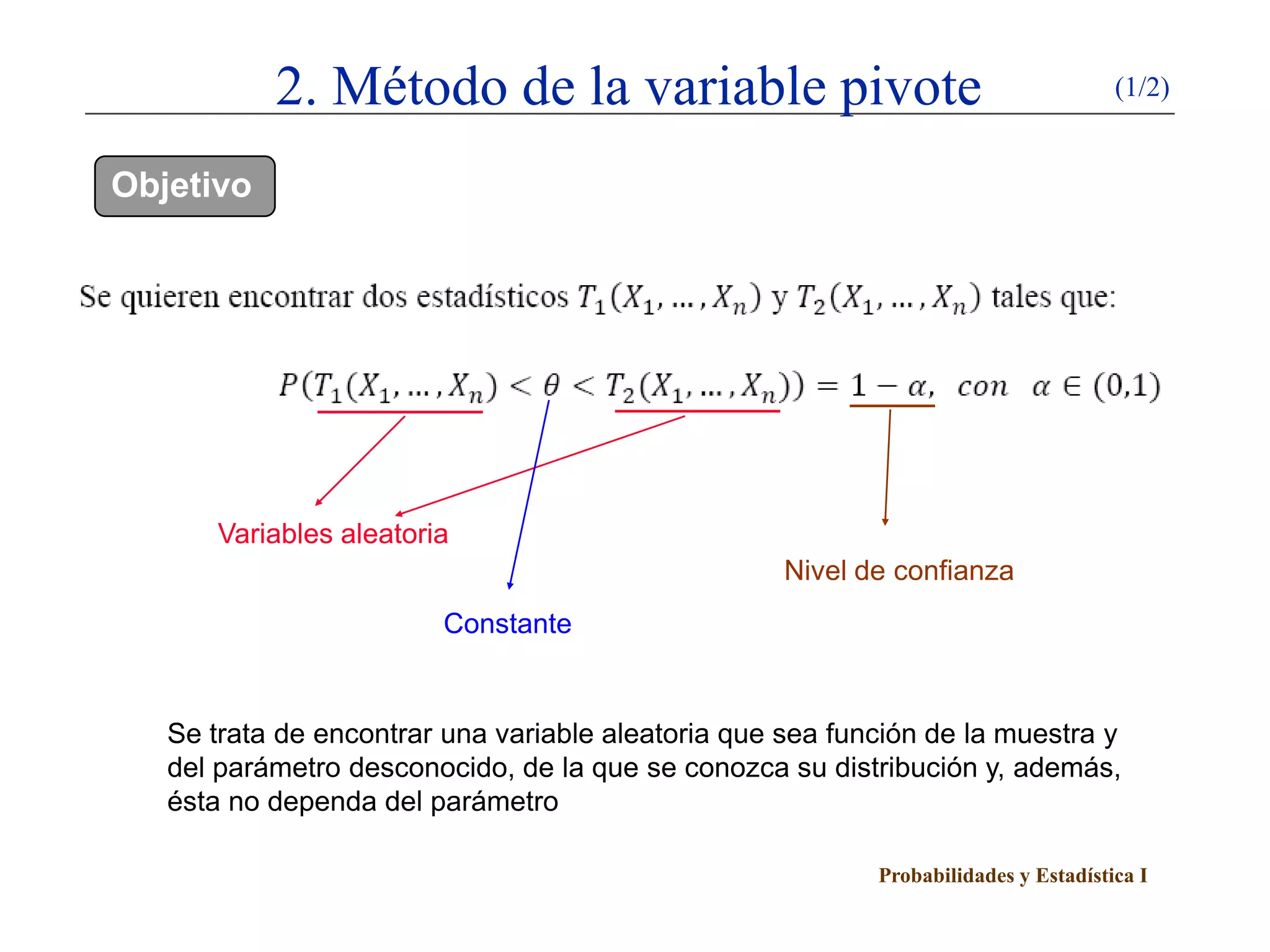
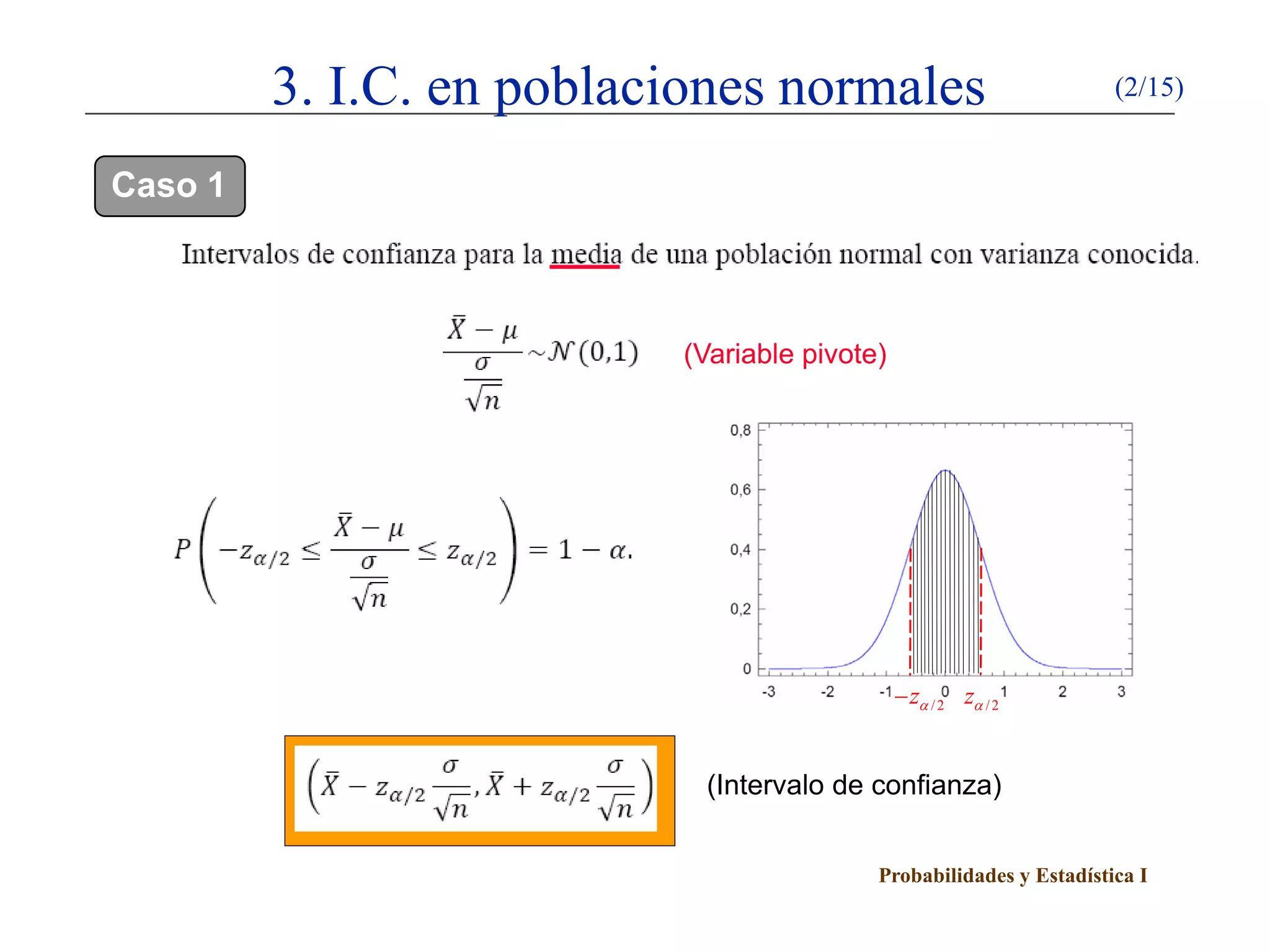
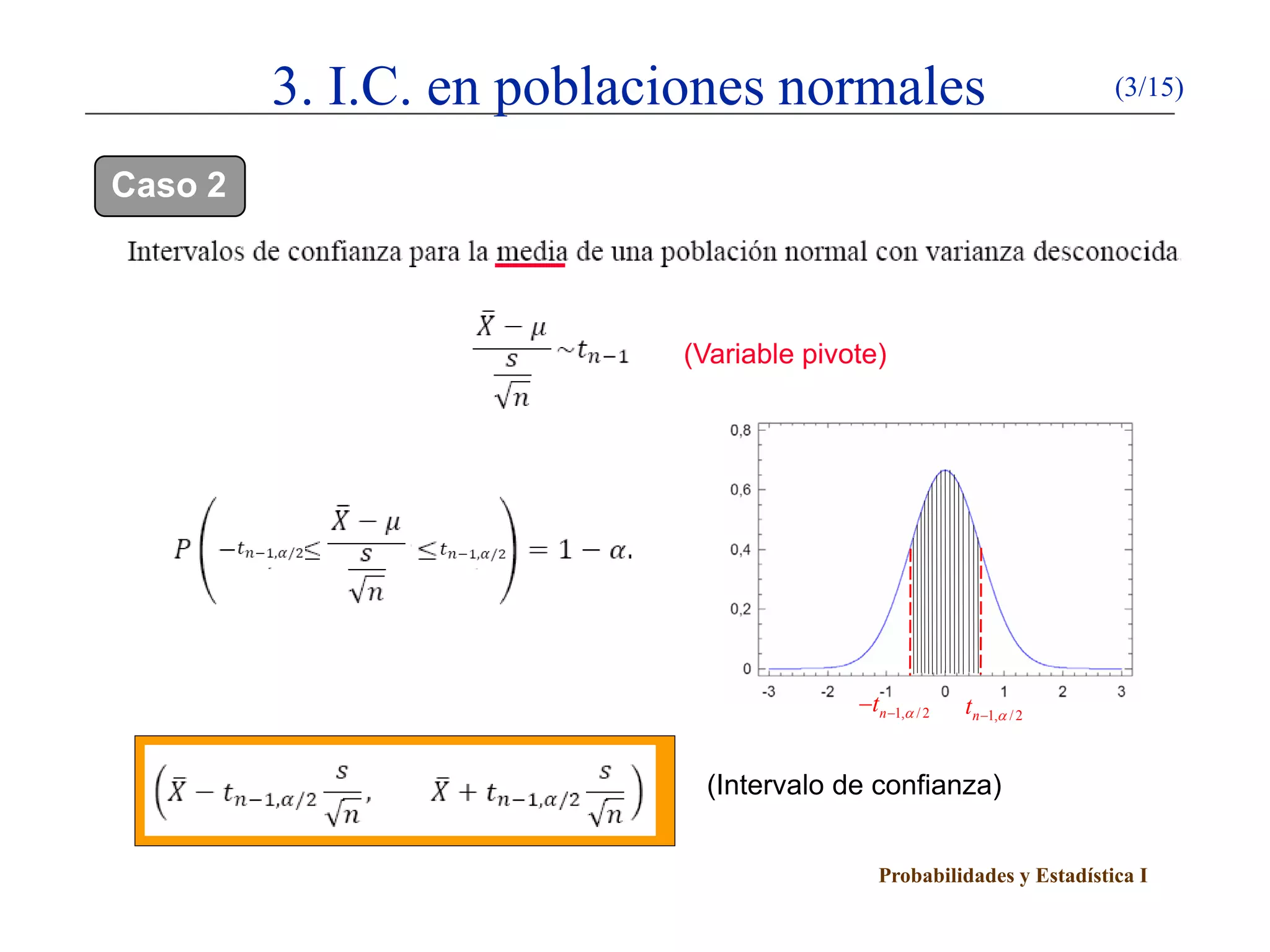
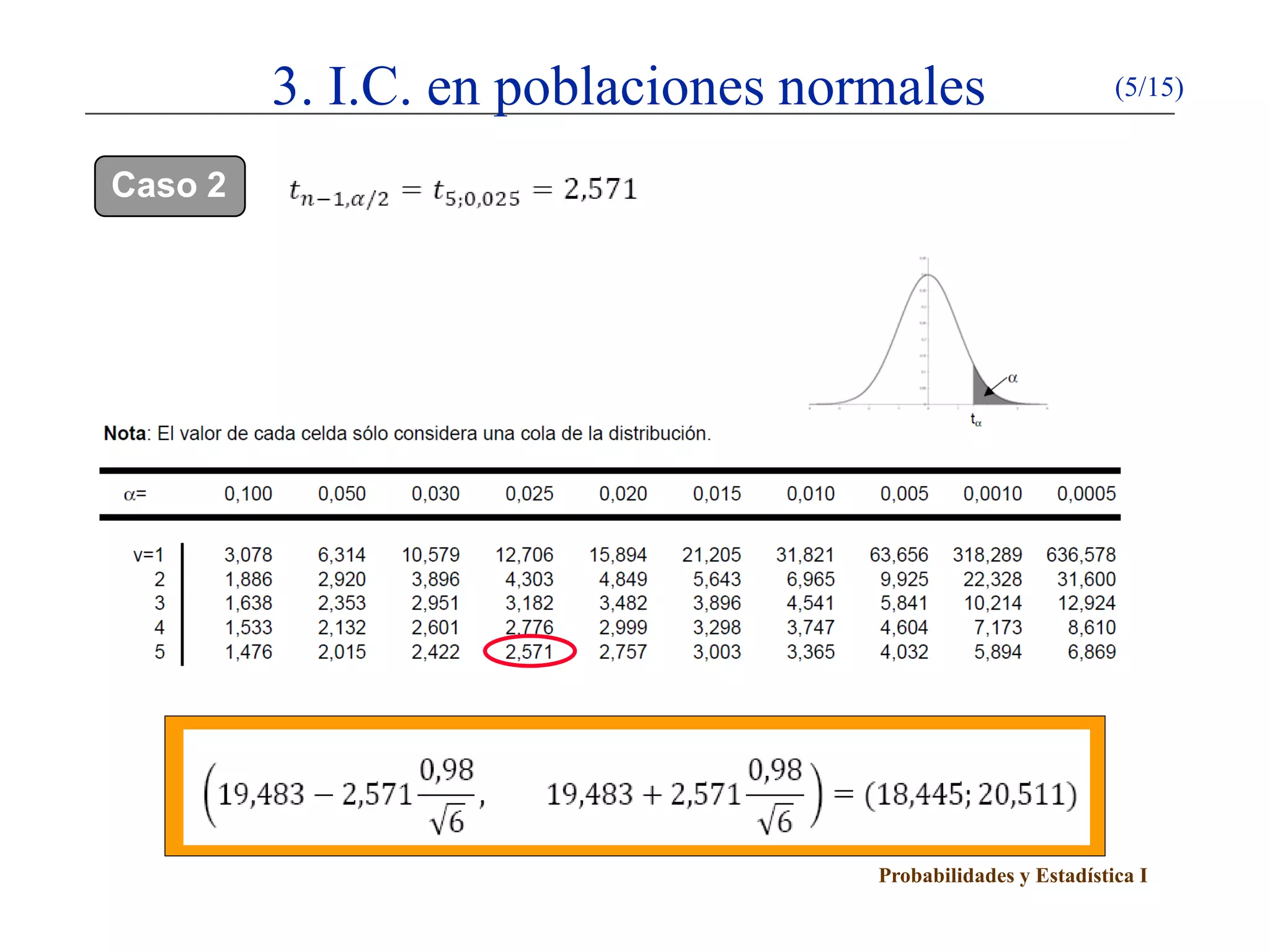
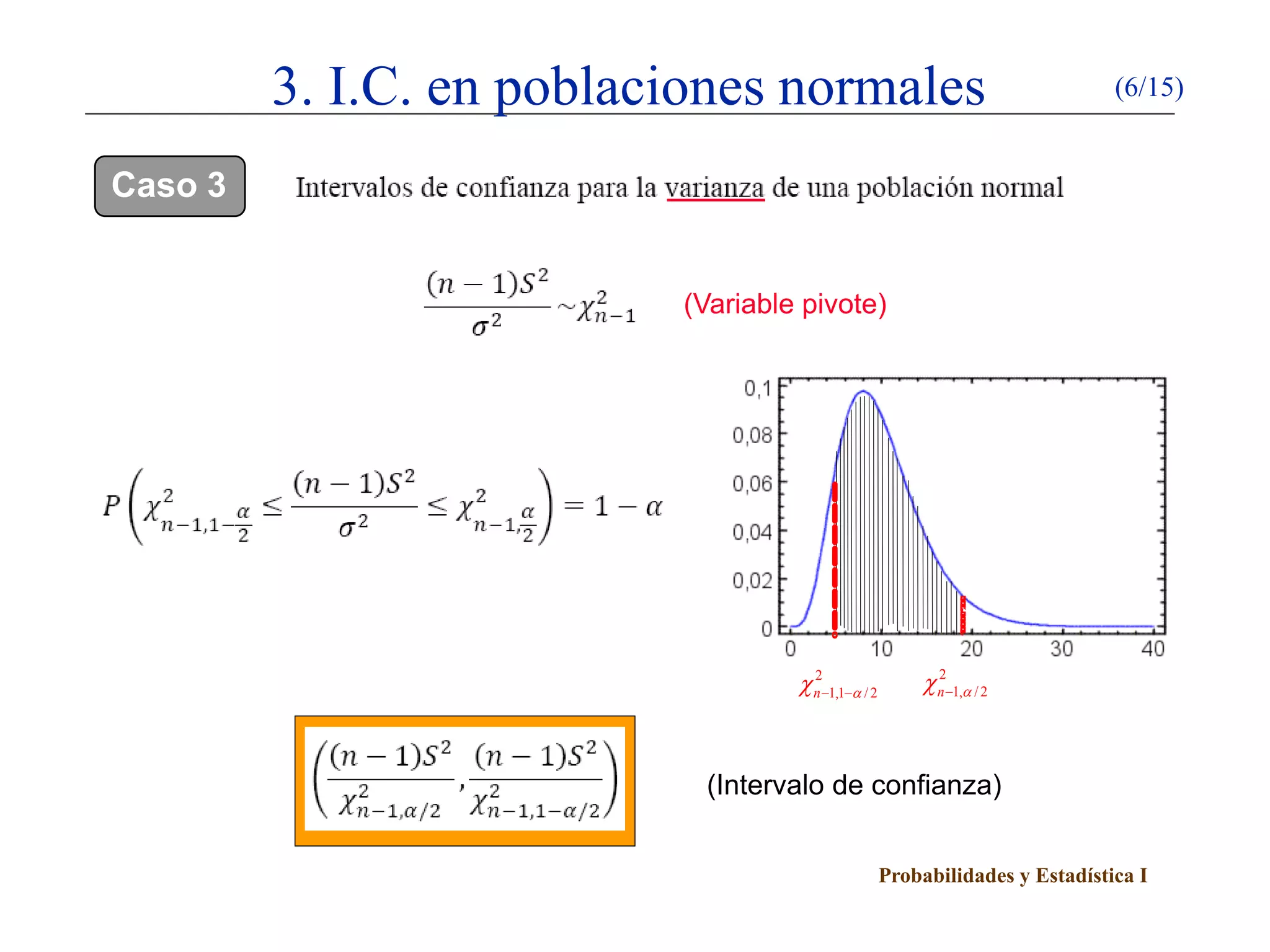
Este documento presenta un esquema sobre intervalos de confianza. Explica el método de la variable pivote para construir intervalos de confianza y describe cómo calcular intervalos de confianza para poblaciones normales y proporciones utilizando este método. Detalla cinco casos para poblaciones normales dependiendo de si se conocen o no la media y la varianza poblacional.

1. Probabilidades y Estadística I
TEMA 11
Intervalos de confianza

2. Probabilidades y Estadística I
Esquema inicial
1. Introducción
2. Método de la variable pivote
3. Intervalo de confianza en poblaciones normales
4. Intervalo de confianza asintóticos

3. Probabilidades y Estadística I
Esquema inicial
1. Introducción
2. Método de la variable pivote
3. Intervalo de confianza en poblaciones normales
4. Intervalo de confianza para proporciones

4. Probabilidades y Estadística I
1. Introducción (1/3)
0 1 2 3 4
0
0,2
0,4
0,6
0,8
1
1,2
( , )Erlang k λ
Asignación

5. Probabilidades y Estadística I
1. Introducción (2/3)
0 1 2 3 4
0
0,2
0,4
0,6
0,8
1
1,2
( , )Erlang k λ
Problemas
1. Determinar el valor de los parámetros a
partir de los datos (Estimación puntual)
( )1 2
ˆ ˆ , ,..., nk k X X X= ( )1 2
ˆ ˆ , ,..., nX X Xλ λ=
1. Determinar el valor de los parámetros a
partir de los datos (Estimación intervalar)
( ) ( )1 1 2 2 1 2
ˆ ˆ, ,..., , ,..., 0.90n nP k X X X k k X X X ≤ ≤ =
 
( ) ( )1 1 2 2 1 2
ˆ ˆ, ,..., , ,..., 0.95n nP k X X X k k X X X ≤ ≤ =
 
( ) ( )1 1 2 2 1 2
ˆ ˆ, ,..., , ,..., 0.99n nP k X X X k k X X X ≤ ≤ =
 

6. Probabilidades y Estadística I
1. Introducción (3/3)
Ejemplo Sea X1,X2,…,Xn una muestra aleatoria simple de una
( ,1)N µ
1 2 ... 1
( , )n
n
X X X
X N
n n
µ
+ + +
∼ (Estimador puntual)
(tipificando) (de la tabla)

7. Probabilidades y Estadística I
Esquema inicial
1. Introducción
2. Método de la variable pivote
3. Intervalo de confianza en poblaciones normales
4. Intervalo de confianza asintóticos

8. Probabilidades y Estadística I
2. Método de la variable pivote (1/2)
Objetivo
Variables aleatoria
Constante
Nivel de confianza
Se trata de encontrar una variable aleatoria que sea función de la muestra y
del parámetro desconocido, de la que se conozca su distribución y, además,
ésta no dependa del parámetro

9. Probabilidades y Estadística I
2. Método de la variable pivote (2/2)
Objetivo
Se trata de encontrar una variable aleatoria que sea función de la muestra y
del parámetro desconocido, de la que se conozca su distribución y, además,
ésta no dependa del parámetro

10. Probabilidades y Estadística I
Esquema inicial
1. Introducción
2. Método de la variable pivote
3. Intervalo de confianza en poblaciones normales
4. Intervalo de confianza asintóticos

11. Probabilidades y Estadística I
3. I.C. en poblaciones normales (1/15)
Sea X1,X2,…,Xn una muestra aleatoria simple de una ( , )N µ σ
Casuística
1.
2.
3.
4.
4.1
4.2
5.

12. Probabilidades y Estadística I
3. I.C. en poblaciones normales (2/15)
Caso 1
(Variable pivote)
/2zα/2zα−
(Intervalo de confianza)

13. Probabilidades y Estadística I
3. I.C. en poblaciones normales (3/15)
Caso 2
(Variable pivote)
(Intervalo de confianza)
1, /2nt α−− 1, /2nt α−

14. Probabilidades y Estadística I
3. I.C. en poblaciones normales (4/15)
Caso 2

15. Probabilidades y Estadística I
3. I.C. en poblaciones normales (5/15)
Caso 2

16. Probabilidades y Estadística I
3. I.C. en poblaciones normales (6/15)
Caso 3
(Variable pivote)
2
1, /2n αχ −
2
1,1 /2n αχ − −
(Intervalo de confianza)

17. Probabilidades y Estadística I
3. I.C. en poblaciones normales (7/15)
Caso 3

18. Probabilidades y Estadística I
3. I.C. en poblaciones normales (8/15)
Caso 4
4.1
4.2
2 2 2
1 2σ σ σ= =

19. Probabilidades y Estadística I
3. I.C. en poblaciones normales (9/15)
Caso 4 2 2 2
1 2σ σ σ= =
(Estimador de varianza común)
(Variable pivote)
(Intervalo de confianza)

20. Probabilidades y Estadística I
3. I.C. en poblaciones normales (10/15)
Caso 4 2 2 2
1 2σ σ σ= =

21. Probabilidades y Estadística I
3. I.C. en poblaciones normales (11/15)

22. Probabilidades y Estadística I
3. I.C. en poblaciones normales (12/15)
Caso 4
(Variable pivote)
( ) ( )
1 2
1 2
22 2
1 2
1 2
n n
X Y
t
S S
n n
µ µ
+ − −∆
− − −
∼
+

23. Probabilidades y Estadística I
3. I.C. en poblaciones normales (13/15)
Caso 4

24. Probabilidades y Estadística I
3. I.C. en poblaciones normales (14/15)
Caso 5
(Variable pivote)
(Intervalo de confianza)

25. Probabilidades y Estadística I
3. I.C. en poblaciones normales (15/15)
Caso 5

26. Probabilidades y Estadística I
Esquema inicial
1. Introducción
2. Método de la variable pivote
3. Intervalo de confianza en poblaciones normales
4. Intervalo de confianza asintóticos

27. Probabilidades y Estadística I
4. Intervalos de confianza asintóticos (1/3)
Sea X1,X2,…,Xn una muestra aleatoria simple con n ≥ 30
Casuística
1.
2.

28. Probabilidades y Estadística I
4. Intervalos de confianza asintóticos (2/3)
Caso 1
(Variable pivote. Por T.C.L)
(Intervalo de confianza)
(1 )
,
p p
N p
n
− 
∼  
 

29. Probabilidades y Estadística I
4. Intervalos de confianza asintóticos (3/3)
Caso 2