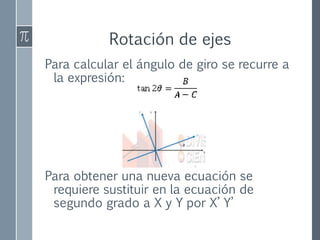
Este documento describe diferentes tipos de transformaciones de coordenadas, incluyendo conversiones entre coordenadas rectangulares y polares, traslación de ejes, y rotación de ejes. Explica cómo realizar estas transformaciones mediante el uso de funciones trigonométricas y el teorema de Pitágoras, y provee ejemplos ilustrativos de cada tipo de transformación.

1. Transformación de
coordenadas
REPÚBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL POPULAR PARA LA EDUCACIÓN UNIVERSITARIA
POLITÉCNICO SANTIAGO MARIÑO
SEDE - CARACAS
Niska Valderrama
C.I:26.497.062

2. Transformación de coordenadas
Consiste en cambiar una relación o
expresión, con el fin de simplificarla.
Si se considera una circunferencia de radio
r cuya ecuación es de forma ordinaria
Si esta circunferencia se coloca en el centro
de origen, su ecuación toma la forma mas
simple.

3. Coordenadas rectangulares a
polares
Las coordenadas rectangulares, están
escritas de la siguiente forma (x,y) y las
polares (r,θ).
En donde r es la distancia desde el origen
hasta el punto y θ el alguno formado por
la línea y el eje X.
Las coordenadas se relacionan
trigonométricamente.

4. Coordenadas rectangulares a
polares
Para este tipo de conversión, se puede usar
la función coseno para encontrar las
coordenadas en y y la función seno para
coordenadas en x.

5. Coordenadas rectangulares a
polares
› Ejemplo: Teniendo las coordenadas
rectangulares x=3 y y=4 ¿Cuál será las
coordenadas polares?
Las coordenadas polares serian

6. Coordenadas polares a
rectangulares
Usando el teorema de Pitágoras, se
encuentra la longitud de la hipotenusa
El Angulo θ se encuentra usando la función
de la tangente

7. Coordenadas polares a
rectangulares
› Ejemplo: Teniendo las coordenadas polares r
=20 y θ= ¿Cuál será las coordenadas
rectangulares?
Las coordenadas rectangulares serian

8. Translación de ejes
El fin de la traslación de ejes es simplificar
la ecuación de una curva para
posteriormente procesarla. Se cambian
los ejes sin girarlos y así cada eje
permanece en paralelo a su posición
original.
Una vez se realice la traslación se cambia el
punto O’(Xo,Yo), además es necesario dar
a cada punto P(x,y) un nuevo conjunto de
coordenadas P’(x’,y’), de acuerdo a las
siguientes relaciones:

9. Translación de ejes
Ejemplo de traslación; Un circulo con centro
en (1,2) y un radio de r=3, se puede
describir por medio de la siguiente
expresión:
Al cambiar los ejes de referencia a O’(1,2),
el mismo circulo se describe como:
También de la siguiente manera:

10. Rotación de ejes
Cambia la rotación de los ejes de referencia
mientras conserva el origen. El principal
motivo de la rotación de ejes es crear una
ecuación mucho mas simple.
Cuando el termino B de la ecuación de
segundo grado es diferente de 0, indica
que los ejes tienen un ángulo con
respecto a al sistema original.

11. Rotación de ejes
Para calcular el ángulo de giro se recurre a
la expresión:
Para obtener una nueva ecuación se
requiere sustituir en la ecuación de
segundo grado a X y Y por X’ Y’

12. Rotación de ejes
Las ecuaciones que permiten esa
sustitución, son las siguientes:

13. Representación grafica
Representación grafica de una
circunferencia en coordenadas polares.

14. Representación grafica
Representación grafica de una parábola en
coordenadas polares.