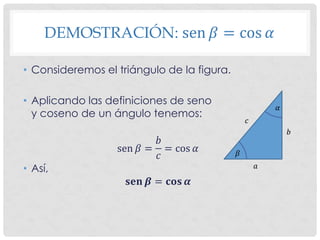
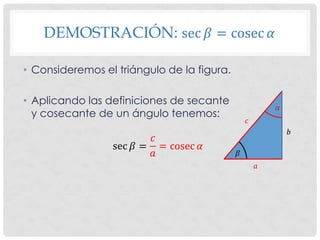
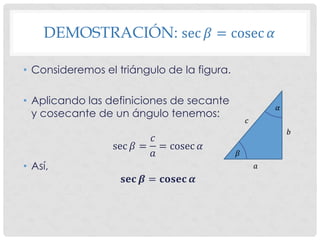
El documento presenta la demostración del Teorema de las Cofunciones, el cual establece que la función trigonométrica de un ángulo es igual a la cofunción del complemento del ángulo. La demostración analiza cada una de las igualdades del teorema (sen β = cos α, sec β = cosec α, tg β = cotg α) utilizando definiciones trigonométricas y considerando los ángulos como ángulos agudos de un triángulo rectángulo.