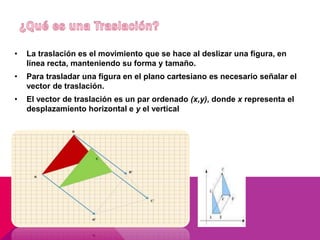
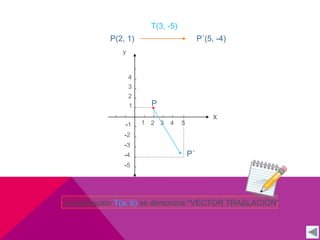
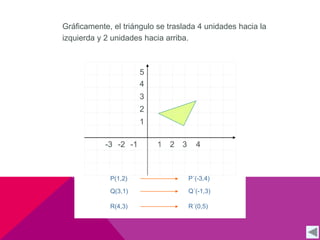
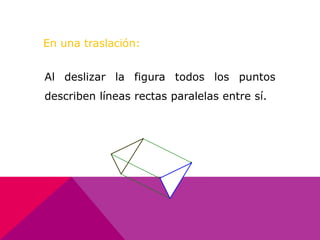
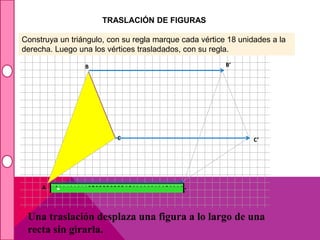
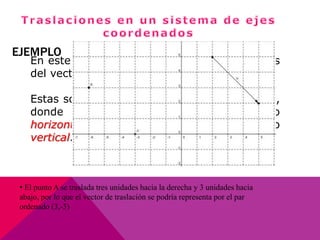
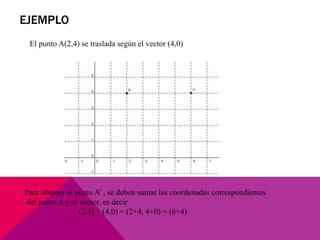
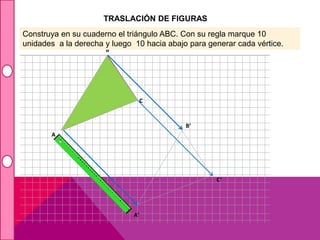
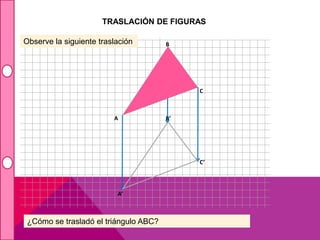
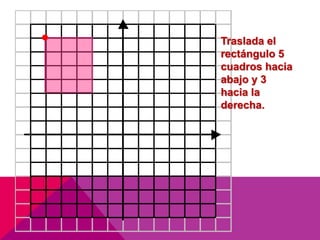
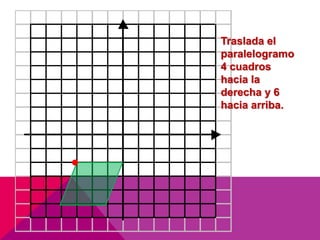
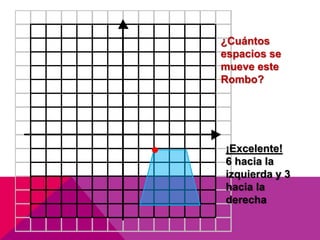
Este documento describe las transformaciones isométricas, que son movimientos que mantienen la forma y el tamaño de una figura geométrica. Existen tres tipos principales: simetrías, traslaciones y rotaciones. Las traslaciones implican deslizar una figura en línea recta manteniendo su forma y tamaño, y se definen mediante un vector de traslación que indica el desplazamiento horizontal y vertical.

2. TRANSFORMACIONES ISOMÉTRICAS
Son movimientos que se pueden realizar con una figura geométrica, a la
cual se le mantiene su forma y tamaño.
La palabra isometría tiene su origen en el griego iso (igual o mismo) y
metria (medir), una definición cercana es igual medida.
Existen tres tipos de transformaciones isométricas:
SIMETRÍA
TRASLACIONES
GIROS O ROTACIONES

3. • La traslación es el movimiento que se hace al deslizar una figura, en
línea recta, manteniendo su forma y tamaño.
• Para trasladar una figura en el plano cartesiano es necesario señalar el
vector de traslación.
• El vector de traslación es un par ordenado (x,y), donde x representa el
desplazamiento horizontal e y el vertical

4. En una traslación se distinguen tres
elementos:
Sentido (derecha, izquierda, arriba, abajo).
Dirección (horizontal, vertical u oblicua).
Magnitud del desplazamiento (distancia entre
la posición inicial y final de cualquier punto)

5. Una traslación en el plano,
.
corresponde a una aplicación T(a, b) que transforma un punto
P(x,y), en otro P´(x + a, y + b ).
P(x, y)
T(a, b)
P´( x + a, y + b )
Ejemplo 1:
P(2, 1)
T(3, -5)
P´(2 + 3, 1 + -5)
P´(5, -4)

6. T(3, -5)
P(2, 1) P´(5, -4)
4
3
2
1
y
-1 1 2 3
x
4 5
-2
-3
-4
-5
P
P´
La aplicación T(a, b) se denomina “VECTOR TRASLACIÓN”

7. Ejemplo 2:
El triángulo PQR, de vértices P(1,2), Q(3,1) y R(4,3) se
“traslada” al aplicar el vector traslación T(-4,2),
y las coordenadas de sus nuevos vértices son: P´, Q´ y R´.
P(1,2)
T(-4,2)
P´(-3,4)
Q(3,1) Q´(-1,3)
R(4,3) R´(0,5)

8. Gráficamente, el triángulo se traslada 4 unidades hacia la
izquierda y 2 unidades hacia arriba.
1
5
4
3
2
1
-3 -2 -1 2 3 4
P(1,2) P´(-3,4)
Q(3,1) Q´(-1,3)
R(4,3) R´(0,5)

9. En una traslación:
Al deslizar la figura todos los puntos
describen líneas rectas paralelas entre sí.

10. Construya un triángulo, con su regla marque cada vértice 18 unidades a la
derecha. Luego una los vértices trasladados, con su regla.
B
C
A’
B’
C’
TRASLACIÓN DE FIGURAS
A
Una traslación desplaza una figura a lo largo de una
recta sin girarla.

11. EJEMPLO
En este caso se debe señalar las coordenadas
del vector de traslación.
Estas son un par ordenado de números (x,y),
donde x representa el desplazamiento
horizontal e y representa el desplazamiento
vertical.
• El punto A se traslada tres unidades hacia la derecha y 3 unidades hacia
abajo, por lo que el vector de traslación se podría representa por el par
ordenado (3,-3)

12. EJEMPLO
El punto A(2,4) se traslada según el vector (4,0)
Para obtener el punto A’ , se deben sumar las coordenadas correspondientes
del punto A y el vector, es decir
(2,4) + (4,0) = (2+4, 4+0) = (6+4)

13. TRASLACIÓN DE FIGURAS
Construya en su cuaderno el triángulo ABC. Con su regla marque 10
unidades a la derecha y luego 10 hacia abajo para generar cada vértice.
B
A’
B’
C’
A
C

14. TRASLACIÓN DE FIGURAS
A
B
C
A’
B’
C’
Observe la siguiente traslación
¿Cómo se trasladó el triángulo ABC?

15. EN GENERAL
Si al punto P(x, y) se le aplica una traslación según el vector (a, b), las
coordenadas de P’ están dadas por P’(x+a, y+b)

16. Traslada el
rectángulo 5
cuadros hacia
abajo y 3
hacia la
derecha.

17. Traslada el
paralelogramo
4 cuadros
hacia la
derecha y 6
hacia arriba.

18. ¿Cuántos
espacios se
mueve este
Rombo?
¡Excelente!
6 hacia la
izquierda y 3
hacia la
derecha