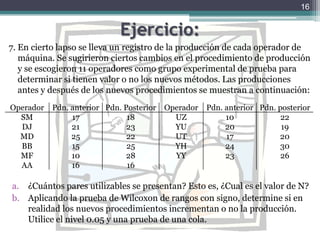
Este documento presenta información sobre estadística no paramétrica, incluyendo cuatro tipos de pruebas libres de distribución (prueba U de Mann-Whitney, prueba de Kruskal-Wallis, prueba Wilcoxon y prueba de rangos con signo de pares ajustados), así como ejemplos y ejercicios para aplicar cada prueba. El objetivo es que los estudiantes aprendan a seleccionar y utilizar los mejores métodos estadísticos no paramétricos para resolver problemas relacionados con la

1. Materia: Estadística Administrativa II Unidad V: “ESTADISTICA NO PARAMETRICA” Maestra: Ing. Elsa Edith Figueroa Rodríguez 1 INSTITUTO TECNOLOGICO SUPERIOR DE CANANEA Licenciado en Administración.

2. Unidad V: Estadística no paramétrica Objetivo:El alumno aprenderá las ventajas y desventajas de utilizar las estadística no paramétricas así como utilizar los mejores criterios de selección para resolver problemas relativos a la administración y tomar mejores decisiones. 2

3. Unidad V: Estadística no paramétrica Estos ensayos exigen que las respuestas se ordenen por rangos de bajo a alto. Se consideran cuatro tipos de pruebas libres de distribución que necesitan ordenación por rango: 3 Kruskal-Wallis Pruebas Wilcoxon U de Mann Withney

4. PRUEBA U DE MANN-WHITNEY Es útil cuando dos conjuntos aleatorios independientes de observaciones muestrales, son por lo menos de nivel ordinal (que puedan ordenarse de alto a bajo o viceversa). El objetivo es determinar si las dos muestras independientes provienen o no de la misma población. Muestras menores que 20 son pequeñas. 4

5. PRUEBA U DE MANN-WHITNEY Estadístico de prueba: n1 (n1 + 1) 2 n2 (n2 + 1) 2 Donde: n1: tamaño de la primer muestra. n2: tamaño de la otra muestra. ΣR1: Sumatoria de rangos de muestra 1. ΣR2: Sumatoria de rangos de muestra 2. 5 U = n1n2 + - ΣR1 U’ = n1n2 + - ΣR2

6. Ejemplo: 1. Existe interés en determinar si existe diferencia en la aptitud mecánica entre los trabajadores de sexo masculino o femenino en una línea industrial de ensamble. Para resolver el asunto, se seleccionaron al azar 9 hombres y 5 mujeres y se sometió a cada persona a una prueba de aptitud mecánica. Utilice el nivel de significación 0.05. Hombres: Puntuaciones: 1500, 1600, 670, 800, 1100, 800, 1320, 1150, 600. Mujeres: Puntuaciones: 1400, 1200, 780, 1350, 890. 6

7. Ejercicio: 2. En una firma se imparte, bajo el auspicio de una organización, un curso sobre los principios de administración, a un grupo de subgerentes y supervisores. Las muestras aleatorias de las puntuaciones obtenidas son: Grupo 1: Subgerentes: 121, 180, 122, 160, 141, 97, 212, 186. Grupo 2: Supervisores: 128, 197, 180, 126, 167, 99, 147. Se sabe que la población de puntuaciones no se distribuye normalmente. Por tanto, no puede aplicarse la prueba t de Student y se utiliza una prueba U de Mann-Whitney de dos colas y nivel 0.05: Establezca Ho y H1. ¿Cuál es el valor crítico? Muestre las regiones de aceptación y rechazo. Asigne rangos a las puntuaciones de menor a mayor, calcule U y U´y tome una decisión. 7

8. PRUEBA U DE MANN-WHITNEY para muestras grandes Una de las muestras es mayor o igual a veinte observaciones. Estadístico de prueba: n1 + n2 + 1) 2 n1 + n2 + 1) 3 8 ΣR1 – ΣR2 - (n1 – n2) Z = n1n2

9. Ejemplo: 3. Supóngase que 20 mujeres y 15 hombres se someten a una prueba de aptitud mecánica. Las calificaciones de tal aptitud se clasificaron en los siguientes rangos. ¿Existe alguna diferencia significativa en la aptitud mecánica entre mujeres y hombres? Se emplea el nivel 0.05. 9

10. Prueba de Kruskal-Wallis: Análisis de varianza por rangos. Prueba no paramétrica que solo necesita datos a nivel ordinal (por rangos). Tal prueba no exige suposiciones respecto a la forma de las poblaciones. Para que sea aplicable, las muestras seleccionadas deben ser independientes. Pasos: Se combinan todos los valores de la muestra. Se ordenan de menor a mayor. Los valores ordenados se reemplazan por rangos principiando con 1 para el valor mas bajo. 10

11. Prueba de Kruskal-Wallis: Análisis de varianza por rangos. Estadístico de prueba: 12 (ΣR1)²(ΣR2)²(ΣRk)² N(N + 1) n1 n2 nk Con k-1 grados de libertad, donde: k : numero de población. ΣR1, ΣR2,…ΣRk : Suma de rangos de las muestras 1, 2, …k n1, n2, … nk : Tamaño de muestras 1, 2, … k N : numero combinado de observaciones para todas las muestras. 11 H = + +...+ - 3(N+1)

12. Ejemplo: 4. Se va a llevar a cabo un seminario de administración para un gran número de ejecutivos de manufactura, finanzas y comercio. Antes de programar las sesiones del seminario, el director del seminario se intereso en determinar si los tres grupos tenían conocimientos semejantes sobre los principios de administración o gerenciales. Se planea tomar muestras de los ejecutivos de manufactura, finanzas y comercio, y aplicar una prueba a cada uno. Si no existe diferencia entre las tres distribuciones, el director del seminario impartirá una sola sesión. Sin embargo, si se encuentra diferencia en las puntuaciones, se impartirán sesiones separadas. El director del seminario selecciona 0.05 como nivel de riesgo. Las puntuaciones de la prueba son las siguientes: 12

13. Ejercicio: 5. El gerente regional del banco de México esta interesado en el índice de cambios o movimiento de las cuentas personales de cheques en cuatro de los bancos filiales. Se pregunta si hay o no diferencia en los índices de movimiento entre los cuatro bancos filiales. (El índice de movimiento es la rapidez con la que el dinero de una cuenta se deposita y retira. Una cuenta extremadamente activa puede tener un índice de 300; pero si solo se giran uno o dos cheques, el índice puede ser de aproximadamente 30.) Los índices de movimiento de las muestras seleccionadas de los cuatro bancos filiales son: Usando el nivel 0.01 y la prueba de Kruskal-Wallis, determine si hay diferencia en los índices de movimiento de las cuentas personales de cheques entre las cuatro filiales. 13

14. PRUEBA DE WILCOXON DE RANGOS CON SIGNO DE PARES AJUSTADOS PARA DIFERENCIAS Se necesita que los datos estén a escala ordinal y que las dos muestras se relacionen (por pares). Pasos necesarios para aceptar o rechazar Ho: Calcular la diferencia entre los dos modelos para cada una de las muestras. En adelante, solo se consideraran los cambios + ó – (no ceros). Se ordenan las diferencias absolutas de menor a mayor (sin importar el signo). Poner rango a las diferencias absolutas. Se determina la media aritmética de las clasificaciones repetidas. A cada rango asignado se le da el signo de la diferencia original. Se suman todos los rangos + y – (sin tomar en cuenta el signo). La menor de las dos sumas se denomina “T calculada”. 14

15. Ejemplo: 6. Se seleccionó una muestra aleatoria de 7 parejas de “jóvenes profesionales urbanos” que eran propietarias de sus casas. El tamaño de una casa de dichos jóvenes se compara con la de sus padres, en función de extensión en pies cuadrados. Al nivel de significación de 0.05, ¿se puede concluir que los jóvenes viven en casa más extensas? 15

16. Ejercicio: 7. En cierto lapso se lleva un registro de la producción de cada operador de máquina. Se sugirieron ciertos cambios en el procedimiento de producción y se escogieron 11 operadores como grupo experimental de prueba para determinar si tienen valor o no los nuevos métodos. Las producciones antes y después de los nuevos procedimientos se muestran a continuación: ¿Cuántos pares utilizables se presentan? Esto es, ¿Cual es el valor de N? Aplicando la prueba de Wilcoxon de rangos con signo, determine si en realidad los nuevos procedimientos incrementan o no la producción. Utilice el nivel 0.05 y una prueba de una cola. 16

17. ¿PREGUNTAS? 17

18. 18