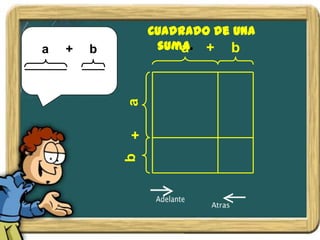
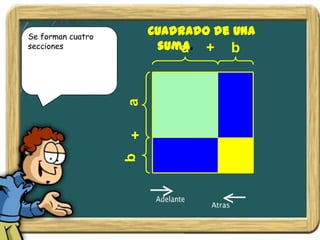
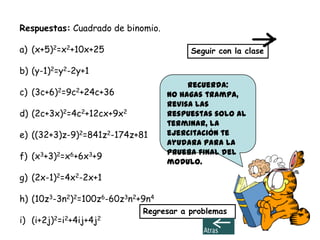
Este documento presenta un nuevo método de aprendizaje interactivo en el que el estudiante es el protagonista de su propio aprendizaje. Introduce a los personajes que ayudarán al estudiante: el profesor SAM dará las clases, Garfield entregará ejercicios, y Odie evaluará al estudiante después de aprender los contenidos.

1. Bienvenido a esta nueva manera de
aprender, en la que tu serás el
protagonista de tu propio aprendizaje,
ahora te invito a conocer a los
personajes que te ayudaran en el
recorrido.

2. Hola, soy el profesor SAM, yo seré el encargado de
darte las clases en este modulo.
Recuerda que en el transcurso de tu trabajo podrás
ver botones como:
Para avanzar en la clase.
Para retroceder la diapositiva.
Para ir al inicio de la presentación.
Seguir con la clase
Para seguir con la clase después de
ver las respuestas de algunos ejercicios.
En algunos momentos podrás hacer clic encima de los
personajes, para acceder a “Respuestas de
ejercicios, o “Comenzar con una prueba”, entre otros.

3. Hola de nuevo, yo soy Garfield,
a mi me toca la tarea de entregarte
ejercicios de cada contenido que te
pase Sam durante esta clase. Espero
que tengas constancia en tu trabajo,
nos vemos mas adelante.

4. Hola, yo soy Odie, soy el encargado
de evaluarte cuando hallas
terminado de asimilar los
contenidos de esta clase, te
recomiendo que desarrolles los
ejercicios que te entregara
Garfield, porque recuerda:
“La practica hace al Maestro”

5. Nociones Básicas:
Para empezar, me gustaría que escribas en esta
pizarra lo que tu piensas que son los “productos
notables”.
ESCRIBE AQUI

6. Nociones Básicas:
Nociones Básicas:
Compara tu definición con esta:
Productos Notables:
Son aquellos productos que se rigen por reglas fijas y cuyo
resultado puede hallarse por simple inspección. Se denominan
también "Identidades Algebraicas".
Son aquellos productos cuyo desarrollo es clásico y por esto
se le reconoce fácilmente.
Ahora has click en “Adelante”
para conocer el contenidos que
vamos a tratar:

7. Nociones Básicas:
Contenido:
Este será el tema que
Cuadrado de una
desarrollaremos en esta suma.
OBJETIVO:
clase, has click en
“Adelante” para comenzar Hallar el cuadrado de una
con la clase
suma.

8. Cuadrado de una
Nociones Básicas:
a + b suma. + b
a
a
b +

9. Se forman cuatro
Cuadrado de una
Nociones Básicas:
secciones suma. + b
a
a
b +

10. Contenido : Cuadrado deBásicas:
Nociones binomio
Analicemos gráficamente el área de este cuadrado por partes:
Los lados son iguales por lo que el área seria (x+y)(x+y) o (x+y)2
Si miramos con atención nos daremos cuenta de:
X Y
X (X·X) (X·Y)
Dos áreas son iguales
por lo que el área total
seria:
Y (X·Y)
(Y·Y)
X2 + 2XY + Y2

11. Contenido 3: Cuadrado de binomio
Nociones Básicas:
Por todo lo anterior, podemos concluir que;
( a b) 2 a2 2ab b 2
En palabras: el cuadrado de un binomio es equivalente al
cuadrado del primer termino mas el doble del producto del
primer por el segundo termino y mas el cuadrado del segundo
termino.
A este producto notable lo vamos a llamar:
“Cuadrado de una suma”

12. Ejercicios: Cuadrado del binomio.
Recuerda: (a+b)2 =
a) (x+5)2=
a2+2ab+c2
b) (y-1)2=
c) (3c+6)2=
d) (2c+3x)2=
e) ((32+3)-9)2=
f) (x+3)2= Acuérdate has
click en mi para
ver las
g) (2x-1)2=
respuestas o sigue
con la clase.
h) (10z-3n)2=
i) (i+2j)2=

13. Respuestas: Cuadrado de binomio.
a) (x+5)2=x2+10x+25 Seguir con la clase
b) (y-1)2=y2-2y+1
Recuerda:
c) (3c+6)2=9c2+24c+36 No hagas trampa,
revisa las
d) (2c+3x)2=4c2+12cx+9x2 respuestas solo al
terminar, la
e) ((32+3)z-9)2=841z2-174z+81 ejercitación te
ayudara para la
prueba final del
f) (x3+3)2=x6+6x3+9
modulo.
g) (2x-1)2=4x2-2x+1
h) (10z3-3n2)2=100z6-60z3n2+9n4
Regresar a problemas
i) (i+2j)2=i2+4ij+4j2

14. Nociones Básicas:
Ahora estas preparado para resolver una prueba
sobre “el cuadrado de un binomio”.

15. Ya has terminado de revisar
los contenidos del cuadrado
de un binomio, ahora aplica tus
conocimientos para lograr
pasar esta prueba.

16. 1. ¿Cuál es el resultado de:?
( a + 4 )2 =
A ( a + 4 )2 = a2 + 4a + 16
2 = a2
B (a+4) + 2a + 8
2 = a2
C (a+4) + 8a + 16

17. 2. ¿Cuál es el resultado de:?
( a + 2b )2 =
A ( a + 2b )2 = a2 + 8ab + 4b2
2 = a2 + 4b2
B ( a + 2b ) + 4ab
2 = a2 + 4b2
C ( a + 2b) + 6ab

18. Has click en
mi para
volver a la
pregunta.

19. Has click en
mi para
volver a la
pregunta.

20. Felicitaciones!!!
Puedes continuar
con la siguiente
pregunta

21. Felicitaciones!!!
Puedes continuar
con la siguiente
pregunta