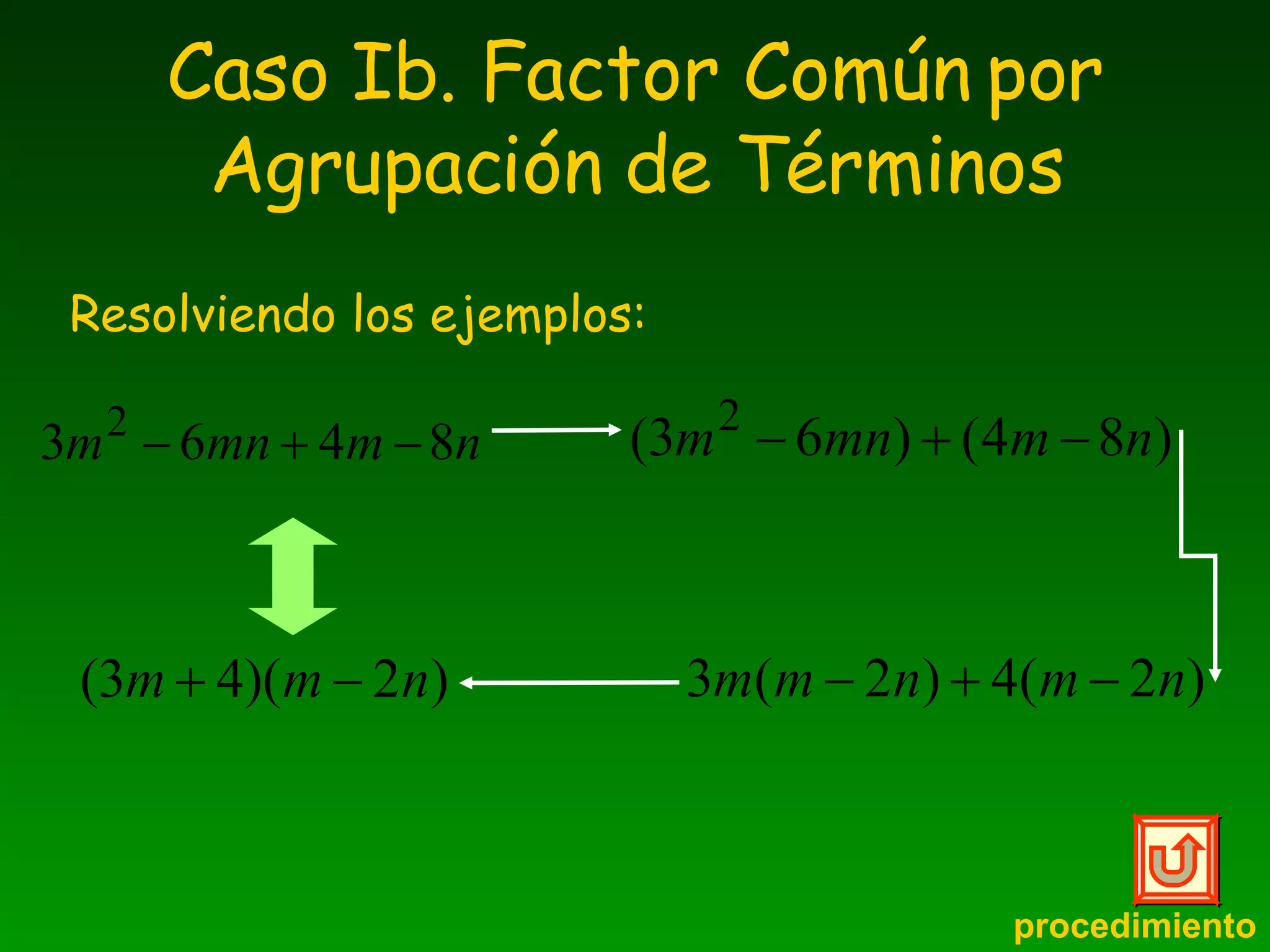
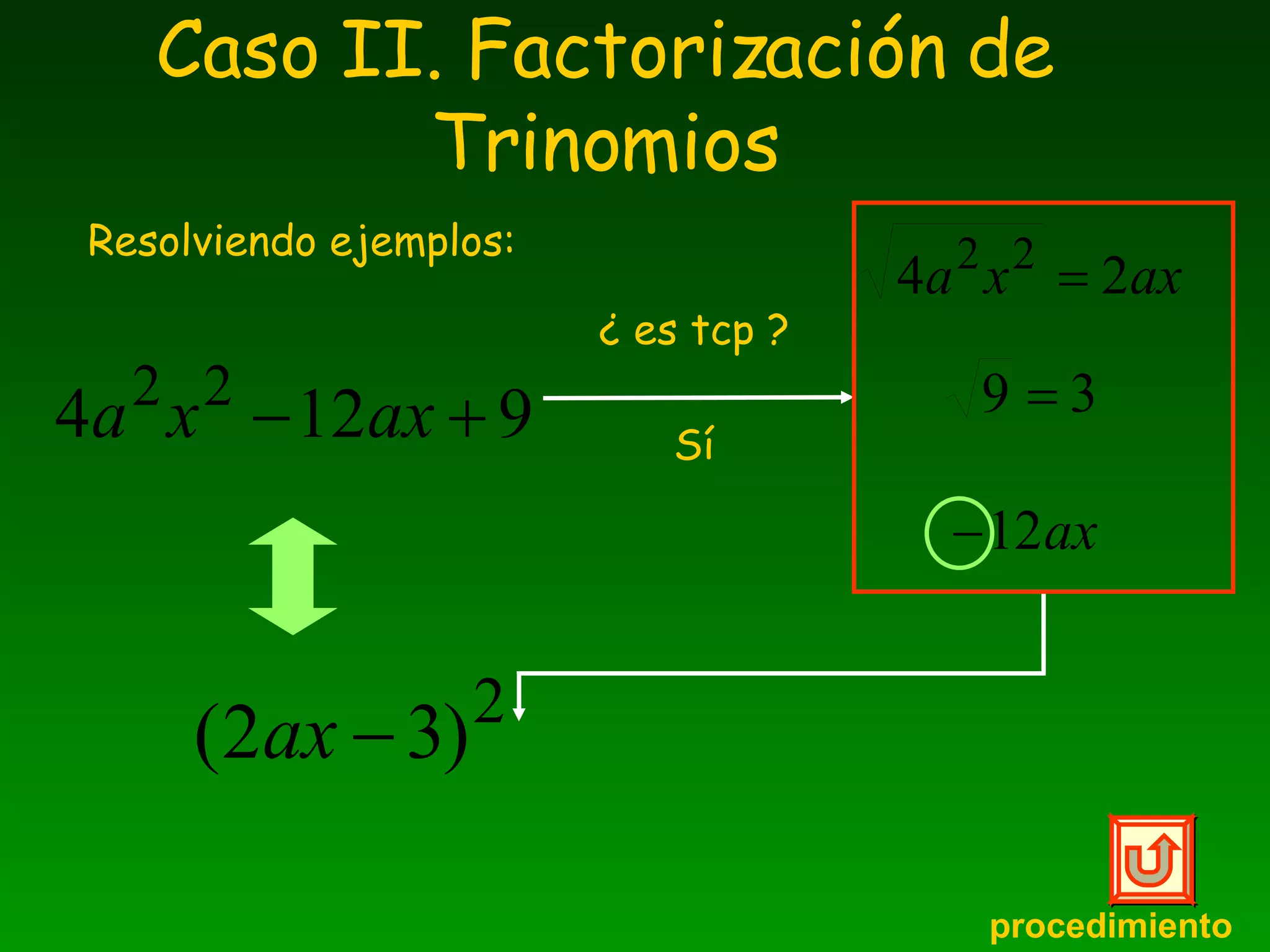
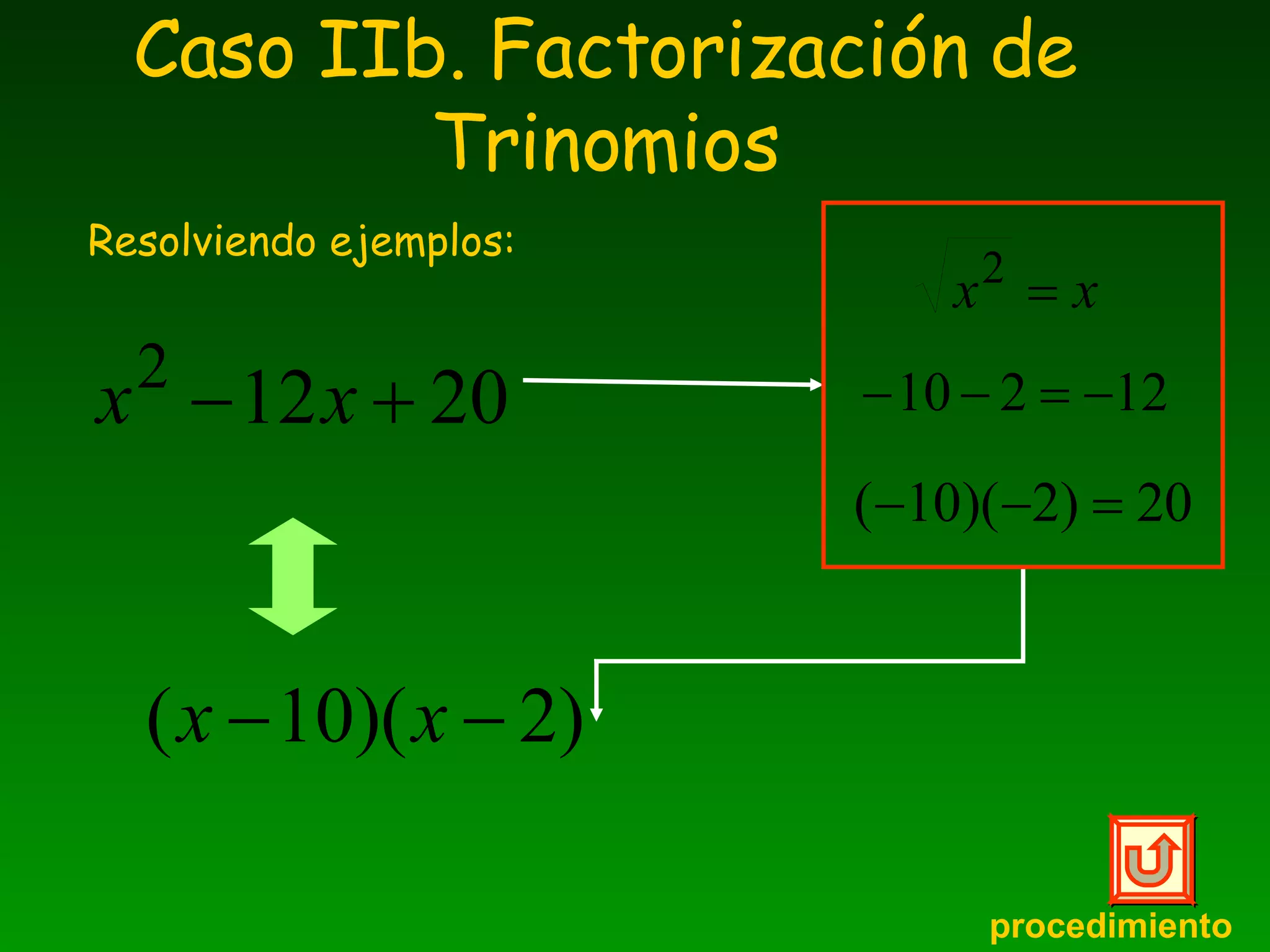
El documento explica diferentes métodos para factorizar expresiones algebraicas, incluyendo factor común, diferencia de cuadrados, trinomios cuadrados perfectos, suma y diferencia de cubos. Detalla los pasos para identificar cada caso y aplicar las propiedades de factorización correspondientes, ilustrando con ejemplos resueltos.

1. Factorización

2. Factorización de diferencia de cuadrados y cubos Factorización Estrategia Factor común y por agrupación Factorización de trinomios

3. Factor Factorización Expresión algebraica que multiplica a una segunda expresión Son factores Operación necesaria para re-escribir una expresión algebraica como producto de factores simples

4. Caso I. Factor Común Aparece en todos los términos de la expresión algebraica, un término común Identificar el máximo término común Dividir la expresión algebraica original entre el máximo término común

5. Caso I. Factor Común Resolviendo los ejemplos: Ejemplo Segundo factor Factorización Máx. factor común

6. Caso Ib. Factor Común por Agrupación de Términos Aparece un término común compuesto después de agrupar términos con factores comunes simples Agrupar términos con factores comunes, usando la propiedad asociativa Factorizar (Caso I) en cada grupo, los factores comunes Identificar el máximo término común Dividir la expresión algebraica entre el máximo término común

7. Caso Ib. Factor Común por Agrupación de Términos Resolviendo los ejemplos: procedimiento

8. Caso Ib. Factor Común por Agrupación de Términos Resolviendo los ejemplos: procedimiento

9. Caso Ib. Factor Común por Agrupación de Términos Resolviendo los ejemplos: procedimiento

10. Caso II. Factorización de Trinomios Trinomio Cuadrado Perfecto Determinar si es tcp Obtener la raíz cuadrada del primer y tercer términos Observar el signo del segundo término Escribir el binomio al cuadrado

11. Caso II. Factorización de Trinomios Resolviendo ejemplos: ¿ es tcp ? Sí procedimiento

12. Caso II. Factorización de Trinomios Resolviendo ejemplos: ¿ es tcp ? Sí procedimiento

13. Caso IIb. Factorización de Trinomios Trinomio de la forma Obtener la raíz cuadrada del primer término Determinar dos números que sumados sean igual a c y que multiplicados sean igual a d Escribir el producto de binomios

14. Caso IIb. Factorización de Trinomios Resolviendo ejemplos: procedimiento

15. Caso II. Factorización de Trinomios Resolviendo ejemplos: procedimiento

16. Caso IIb. Factorización de Trinomios Trinomio de la forma Completar el tcp Factorizar la diferencia de cuadrados resultantes Método general

18. Trinomio Cuadrado Perfecto Resultado del siguiente producto notable: o,

19. Trinomio de la forma Resultado del siguiente producto notable: Donde: y

20. Caso III. Factorización de la Diferencia de Cuadrados Identificar la diferencia de cuadrados Obtener la raíz cuadrada del primer y segundo términos Escribir el producto de binomios conjugados

21. Resolviendo ejemplos: procedimiento Caso III. Factorización de la Diferencia de Cuadrados

22. Resolviendo ejemplos: procedimiento Caso III. Factorización de la Diferencia de Cuadrados

23. Caso IV. Factorización de la Suma o Diferencia de Cubos Identificar si es suma o diferencia de cubos Obtener la raíz cúbica del primer y segundo términos Escribir el producto del binomios por trinomio correspondiente

24. Resolviendo ejemplos: procedimiento Caso IV. Factorización de la Suma o Diferencia de Cubos diferencia

25. Resolviendo ejemplos: procedimiento Caso IV. Factorización de la Suma o Diferencia de Cubos suma

26. Diferencia de Cuadrados Resultado del siguiente producto notable:

27. Suma y Diferencia de Cubos Resultado del siguiente producto notable: o bien,

28. Estrategia General Factorizar todos los factores comunes. Observar el número de términos entre paréntesis (o en la expresión original). Si hay: Cuatro términos: factorizar por agrupación. Tres términos: probar si es tcp y factorizar así; si no es tcp, emplear el caso general. Dos términos y cuadrados: buscar la diferencia de cuadrados y factorizarla. Dos términos y cubos: buscar la suma o diferenica de cubos y factorizar. Asegurarse de que la expresión está factorizada completamente.