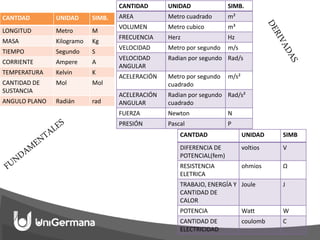
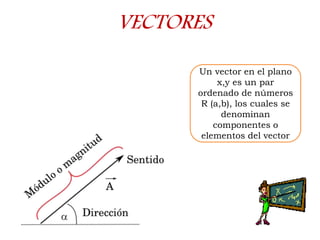
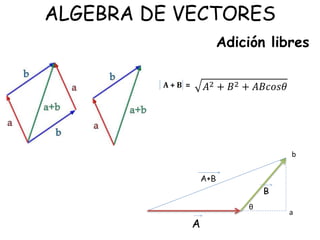
Este documento trata sobre magnitudes y vectores en física. Explica que una magnitud física es una característica cuantificable de un objeto o fenómeno como el tiempo, la masa o la velocidad. Luego define unidades de medida como el metro, el kilogramo y el segundo. Finalmente, introduce conceptos de vectores como su magnitud, dirección y representación gráfica, así como operaciones algebraicas con vectores como suma, resta, producto escalar y producto vectorial.

1. MAGNITUDES Y VECTORES
Lic. Sandra Milena Pachón P.
UPN
FUNDACIÓN UNIVERSITARIA COLOMBO GERMANA
RESOLUCIÓN 26827 DE 29 DE NOVIEMBRE 2017

2. Investiga
Materia energía y
espacio
(no viva)
Relaciones

3. CANTIDADES FÍSICAS
Una magnitud o cantidad física es una característica de
un objeto o un fenómeno físico, que puede ser medida.
Las magnitudes físicas son numerosas y describen los
fenómenos físicos. Son magnitudes físicas: el tiempo, la
masa, la temperatura, la velocidad, el volumen, la
presión, la carga eléctrica, etc.
TOMADO DE: https://coscomantauni.files.wordpress.com/2014/02/02-cantidades-fisicas.pdf

4. CANTDAD UNIDAD SIMB.
LONGITUD Metro M
MASA Kilogramo Kg
TIEMPO Segundo S
CORRIENTE Ampere A
TEMPERATURA Kelvin K
CANTIDAD DE
SUSTANCIA
Mol Mol
ANGULO PLANO Radián rad
CANTIDAD UNIDAD SIMB.
AREA Metro cuadrado m²
VOLUMEN Metro cubico m³
FRECUENCIA Herz Hz
VELOCIDAD Metro por segundo m/s
VELOCIDAD
ANGULAR
Radian por segundo Rad/s
ACELERACIÓN Metro por segundo
cuadrado
m/s²
ACELERACIÓN
ANGULAR
Radian por segundo
cuadrado
Rad/s²
FUERZA Newton N
PRESIÓN Pascal P
CANTDAD UNIDAD SIMB
DIFERENCIA DE
POTENCIAL(fem)
voltios V
RESISTENCIA
ELETRICA
ohmios Ω
TRABAJO, ENERGÍA Y
CANTIDAD DE
CALOR
Joule J
POTENCIA Watt W
CANTIDAD DE
ELECTRICIDAD
coulomb C

5. NOTACIÓN CIENTÍFICA
Debido que en física, es muy usual trabajar con
cantidades muy pequeñas o muy grandes, se utilizan
potencias de 10 para señalar la posición del punto
decimal sin tener que manejar un gran número de
ceros.
21X10−6
in
1,2x106
ft

6. MULTIPLOS Y SUBMULTIPLOS
DEL SI
PREFIJO SIMBOLO MULTIPLICADOR
Tera T 1012
Giga G 109
Mega M 106
Kilo K 103
Unidad base 100
Mili M 10−3
Micro µ 10−6
Nano N 10−9
pico p 10−12

7. La cuarta parte en centímetros de
20 m es:
40 cm
400 cm
4 m
20 cm
1 700 m equivale a:
1 km 7 m
1 km 70 m
1 km 700 m

8. VECTORES
Un vector en el plano
x,y es un par
ordenado de números
R (a,b), los cuales se
denominan
componentes o
elementos del vector

9. LIBRES
SISTEMA DE
COORDENADAS

10. MAGNITUD DE UN VECTOR

11. DIRECCIÓN DE UN VECTOR
CALCULAR MAGNITUD, DIRECCIÓN
Y REPRESENTRALOS EN EL PLANO
CARTESIANO

12. UN VECTOR POR UN ESCALAR
Multiplicar un vector por un escalar α
diferente de cero, tienen el efecto de
multiplicar la longitud del vector por el
vector absoluto de ese escalar
𝛼𝑣 = 𝛼2 𝑎2 + 𝛼2 𝑏2 = 𝛼 𝑎2 + 𝑏2 = 𝛼 |𝑣|
La dirección depende del signo del escalar

13. SUMA

14. RESTA

16. ALGEBRA DE VECTORES
Adición libres
A + B =
θ
a
b
𝐴2 + 𝐵2 + 𝐴𝐵𝑐𝑜𝑠𝜃

17. Adición coordenadas
A+B= i (Ax+Bx)+ j (Ay+By)+ k (Az+Bz)
A+B =

18. Diferencia libres
α
θ
β
A – B = A + (-B)
Dirección
Sen θ / A-B = Sen β /A = Sen α / -B
A - B =

19. Diferencia coordenadas
A - B = i (Ax - Bx)+ j (Ay - By)+ k (Az
- Bz)
A - B =

20. Producto punto o escalar, no se tiene
coordenadas de referencia, ya que es la
Combinación de 2 vectores para conseguir
Un escalar asi:
θ
A. B = A B Cos θ
Es conmutativo A.B = B.A
A = 0 ó B = 0
A.B = 0 si θ = 90° ó θ = 270°
A . A = A² , su ángulo es de 0

21. Producto punto o escalar con coordenadas
A . B = Ax.Bx + Ay.By + Az.Bz
Es conmutativo A.B = B.A

22. Producto vectorial o cruz
A X B = A x B Sen θ
A = 0 ó B = 0
A X B = 0 si θ = 0 es decir, A es paralelo a B
Libres
Coordenadas
i j k
A x B = Ax Ay Az
Bx By Bz

23. Producto por un escalar libres
Producto por un escalar coordenadas
b. B = C
Si b > 0 tiene la misma dirección
Si b< 0 tiene dirección contraria y
sentido
bA = i(bAx) + j(bAy) + k(bAz)
bA =