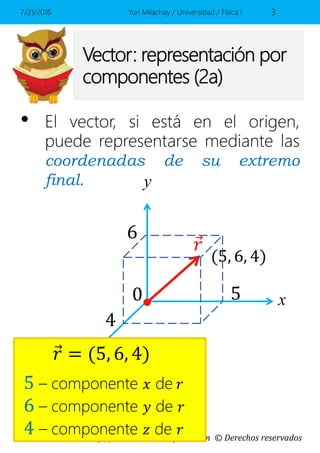
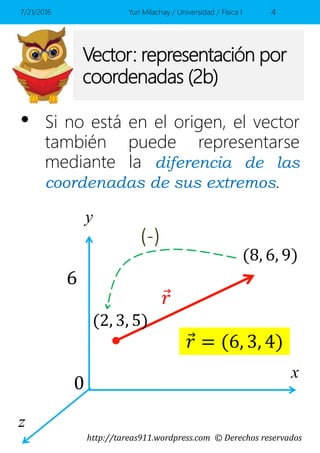
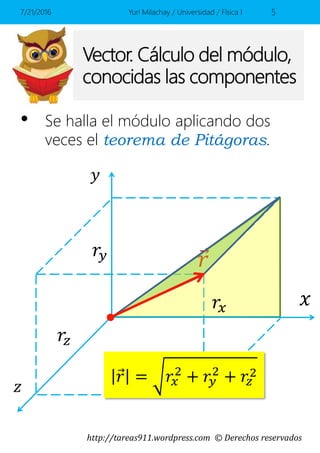
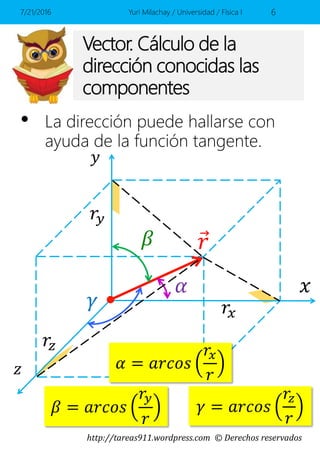
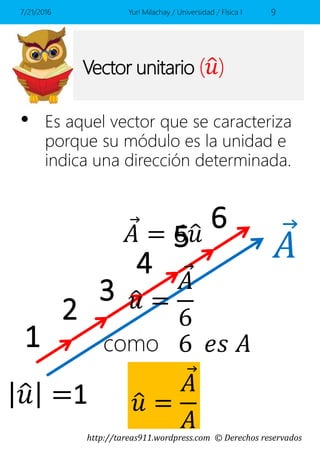
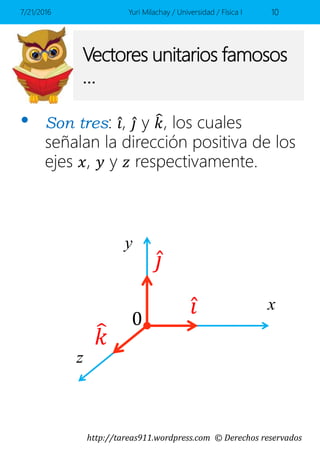
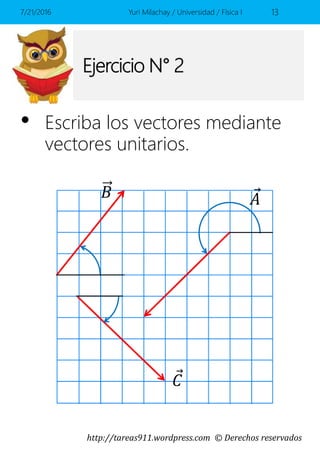
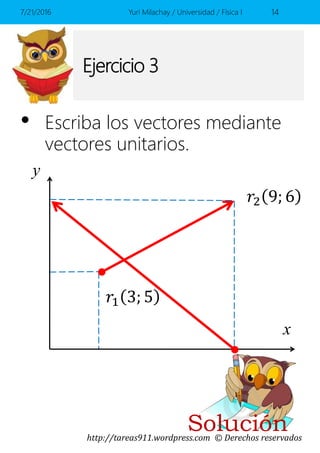
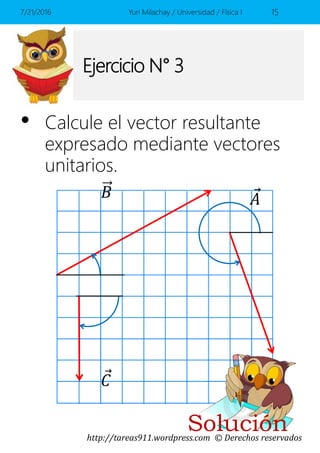
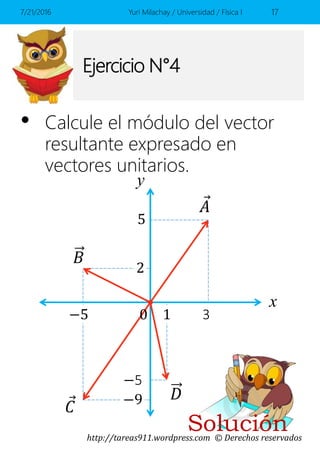
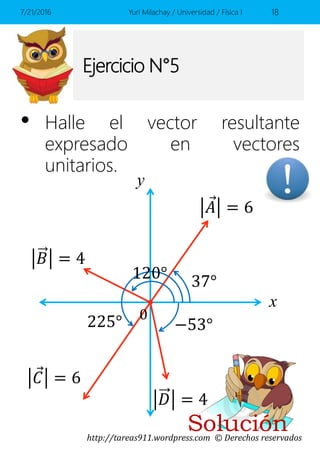
Este documento presenta conceptos básicos sobre vectores en el espacio, incluyendo la representación de vectores mediante componentes y vectores unitarios, y cómo calcular ángulos, módulos y sumas de vectores. Contiene ejemplos y ejercicios resueltos sobre estos temas.