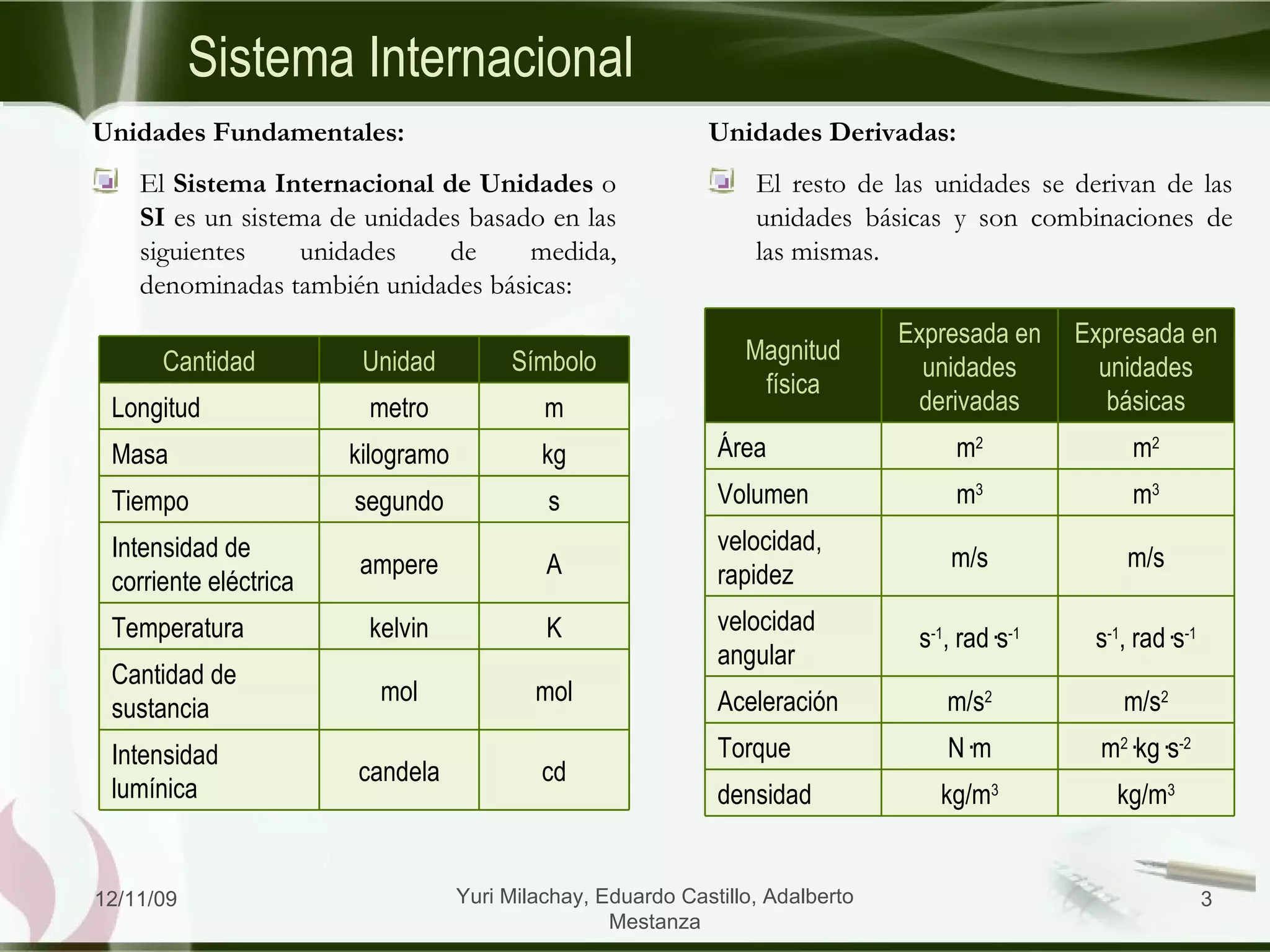
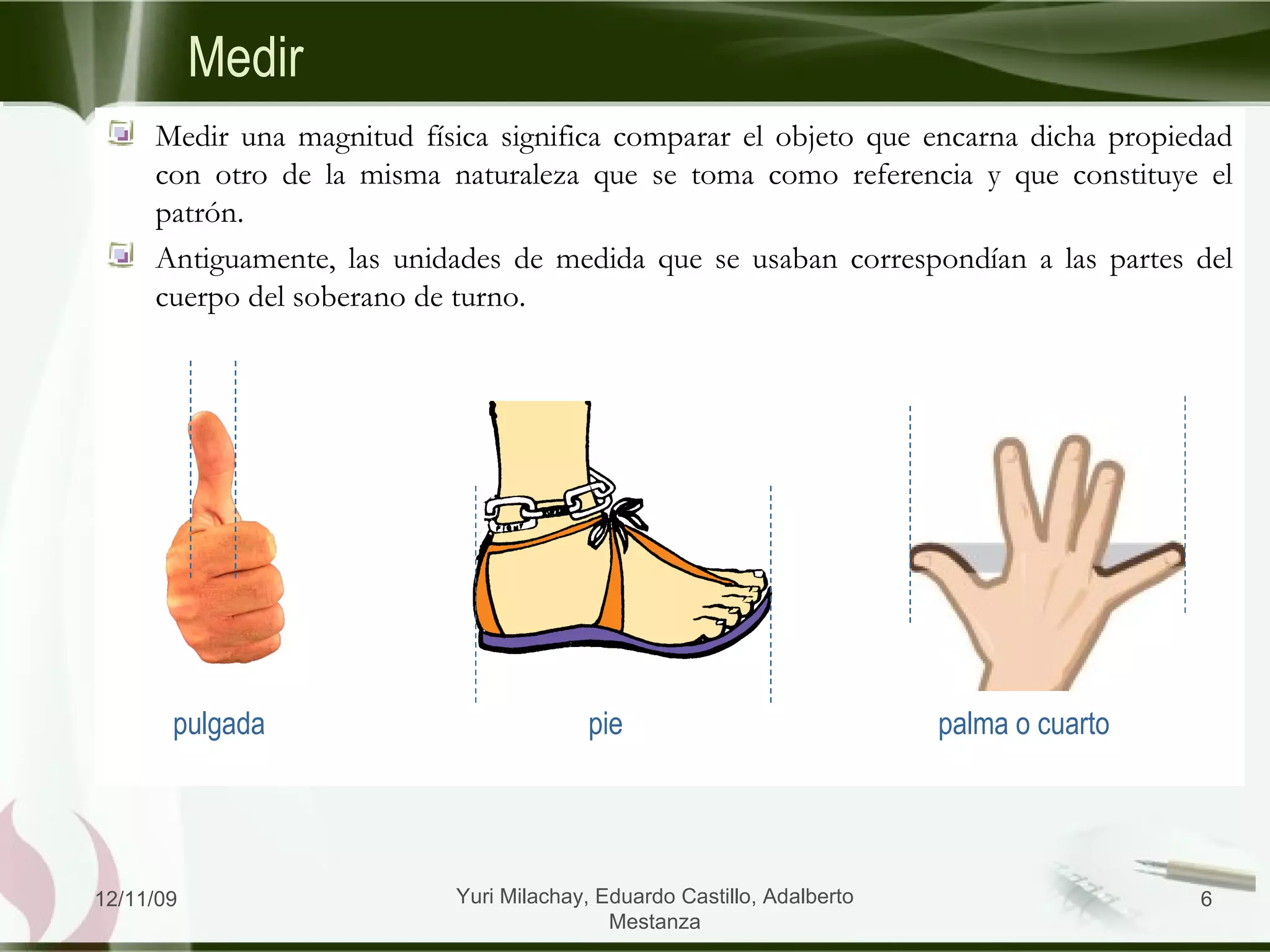
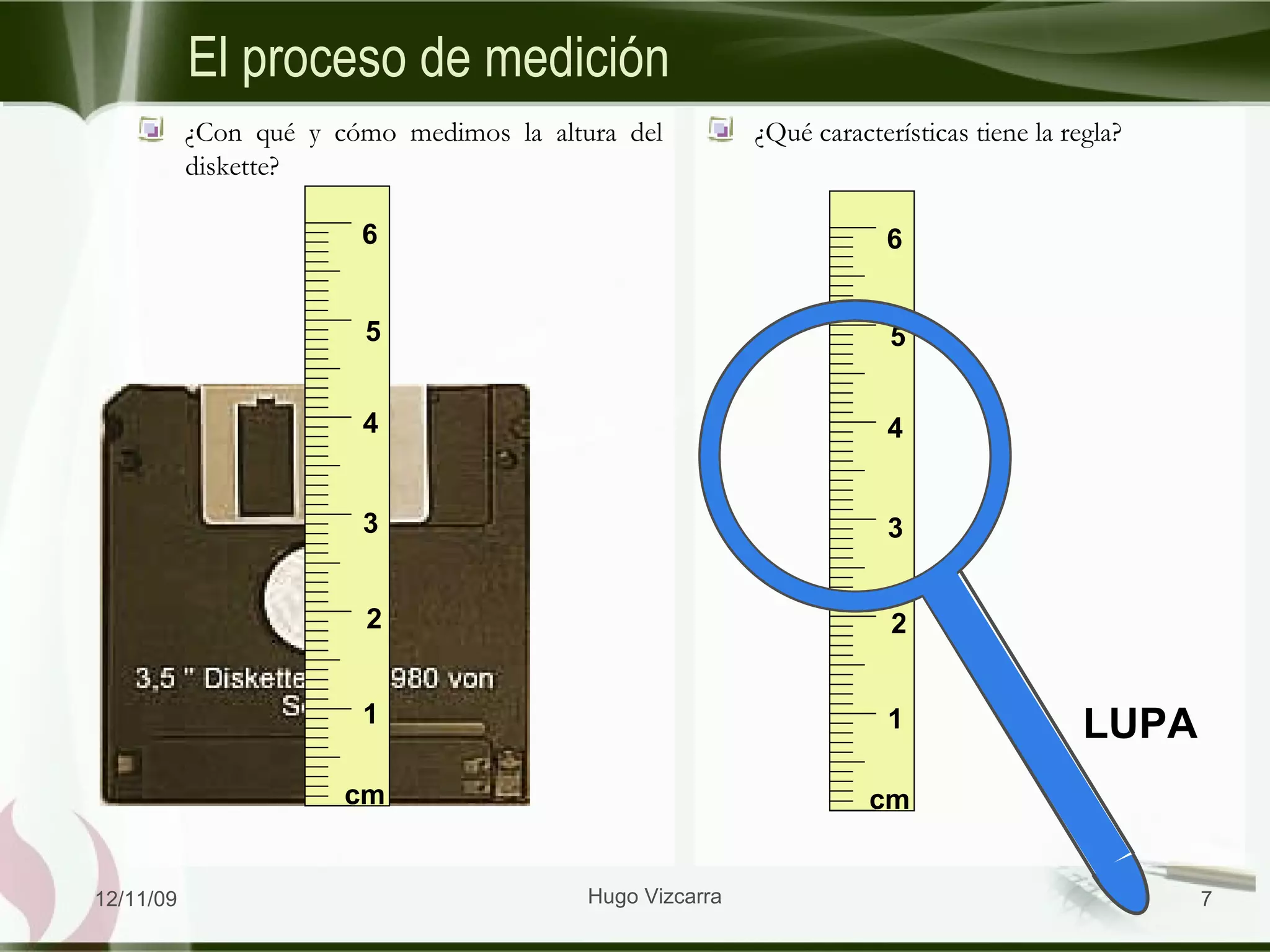
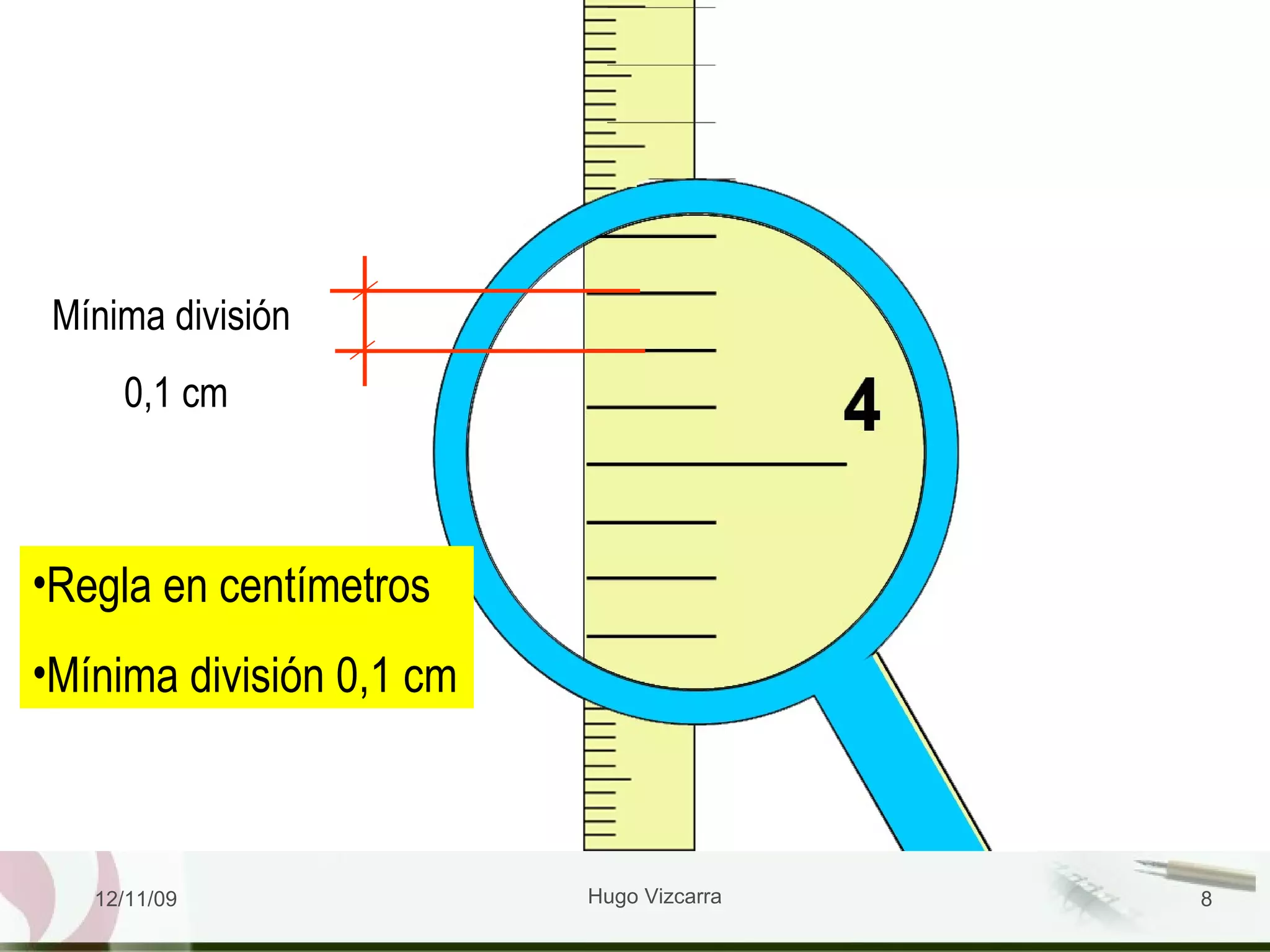
El documento presenta información sobre el Sistema Internacional de Unidades (SI) y conceptos relacionados con la medición y el movimiento en una dimensión. Explica que el SI se basa en 7 unidades fundamentales y describe cada una. También cubre temas como conversiones de unidades, cifras significativas, y el movimiento rectilíneo uniforme.

1. Semana 1 Sistema internacional. Movimiento en una dimensión. MRU. Sistema internacional. Conversión de unidades. Cifras significativas (CS). Operaciones con CS. .

2. Sistema Internacional Magnitud Física Se denominan magnitudes físicas a las propiedades de los cuerpos que son susceptibles a ser medidas. Por ejemplo: la longitud, la masa y el volumen son magnitudes físicas ya que siempre se pueden medir y expresar a través de números: 5,0 metros, 2,0 kilogramos, 6,0 metros cúbicos. Sistemas de unidades Para medir las magnitudes físicas, se necesitan unidades. Las cuales se organizan según el sistema que se emplee. Existen las magnitudes fundamentales , tales como: la longitud, la masa, el tiempo, etc., a partir de las cuales se definen las magnitudes derivadas , entre estas: la velocidad, la aceleración, la fuerza, etc. Cuando se ha elegido ese conjunto reducido y completo de magnitudes fundamentales se dispone entonces de un sistema de unidades. El Sistema Internacional de Unidades (SI) El SI toma como magnitudes fundamentales la longitud, la masa, el tiempo, la intensidad de corriente eléctrica, la temperatura absoluta, la intensidad luminosa y la cantidad de sustancia , y fija las correspondientes unidades para cada una de ellas. A estas siete magnitudes fundamentales hay que añadir dos suplementarias asociadas a medidas angulares, el ángulo plano y el ángulo sólido. 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

3. Sistema Internacional Unidades Fundamentales: El Sistema Internacional de Unidades o SI es un sistema de unidades basado en las siguientes unidades de medida, denominadas también unidades básicas: Unidades Derivadas: El resto de las unidades se derivan de las unidades básicas y son combinaciones de las mismas. 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza Cantidad Unidad Símbolo Longitud metro m Masa kilogramo kg Tiempo segundo s Intensidad de corriente eléctrica ampere A Temperatura kelvin K Cantidad de sustancia mol mol Intensidad lumínica candela cd Magnitud física Expresada en unidades derivadas Expresada en unidades básicas Área m 2 m 2 Volumen m 3 m 3 velocidad, rapidez m/s m/s velocidad angular s -1 , rad·s -1 s -1 , rad·s -1 Aceleración m/s 2 m/s 2 Torque N·m m 2 ·kg·s -2 densidad kg/m 3 kg/m 3

4. Conversión de unidades ¿Cómo proceder para convertir exitosamente unidades de un sistema otro? Ten en cuenta que, al momento de realizar los cálculos de conversión del sistema inglés al SI, es preciso que tomes en cuenta el número de cifras significativas para escribir los resultados. Es importante que tengas a la mano las equivalencias. Para convertir 20 mi/h a km/h, lo que debes hacer es realizar la siguiente operación: Sistema Inglés El Sistema Inglés de Unidades es aún usado ampliamente en los Estados Unidos de América y, cada vez en menor medida, en algunos países de la comunidad británica. Debido a la intensa relación comercial que se tiene con los EUA, existen muchos productos fabricados con especificaciones en este sistema. Ejemplos de ello son los productos de madera, peletería, metal mecánica, motores, electrodomésticos cables conductores y perfiles metálicos. 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

5. Sistema Internacional Equivalencias del SI al Sistema Inglés 1 in = 25,4 mm = 2,54 cm = 0,025 4 m 1 ft = 12 in 1 ft = 0,304 8 m 1 yd = 3 ft = 36 in 1 yd = 0,914 4 m milla (mi) 1 mi = 5 280 ft = 1 760 yd 1 mi = 1,609 km m 1 lb = 4,45 N 1 slug = 14,60 kg 1 J = 0,738 ft  lb 1 Btu = 778 ft  lb = 1 054 J 1 hp = 550 ft  lb/s = 746 W 1 atm = 14,7 lb/in 2 Notación Científica Es la forma de representar las cantidades de modo tal que se ponga en relieve el número de cifras significativas de que consta. Por ejemplo, ¿cómo explicitar que 123 cm es el resultado de una medida y que posee tres cifras significativas? Para hacerlo, se debe escribir la cantidad en potencia de 10, así: 123 cm = 1,23 x 10 2 cm 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

6. Medir Medir una magnitud física significa comparar el objeto que encarna dicha propiedad con otro de la misma naturaleza que se toma como referencia y que constituye el patrón. Antiguamente, las unidades de medida que se usaban correspondían a las partes del cuerpo del soberano de turno. 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza palma o cuarto pie pulgada

7. El proceso de medición ¿Con qué y cómo medimos la altura del diskette? ¿Qué características tiene la regla? 06/09/09 Hugo Vizcarra cm 5 4 3 2 1 6 cm 5 4 3 2 1 6 LUPA

8. 06/09/09 Hugo Vizcarra Mínima división 0,1 cm Regla en centímetros Mínima división 0,1 cm

9. 06/09/09 Hugo Vizcarra L = 4,35 cm + 0,05 cm Dos decimales Los dígitos 4 y 3 son exactos El dígito 5 es dudoso Tres cifras significativas (4, 3 y 5) cm 5 4 3 2 1 6

10. Cifras significativas Son todas las cifras exactas que resultan de la medición más la última cifra que es estimada. 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza 4,35 cm Cifras exactas Cifra estimada Cifras significativas La medida tiene 3 cifras significativas cm 5 4 3 2 1

11. Cifras significativas El total de cifras significativas es independiente de la posición de la coma decimal. Mi estatura es 1,80 m = 18,0 dm = 180 cm 3 cifras significativas La masa de Juan es 50,51 kg = 5,051 x 10 -3 g 4 cifras significativas Los ceros a la izquierda de dígitos no nulos, nunca serán cifras significativas. El botón tiene un diámetro de 28 mm = 0,028 m = 0,000 028 km 2 cifras significativas Los ceros intermedios o al final de dígitos no nulos, siempre serán cifras significativas. 0,000 1050 m 4 cifras significativas 20 066 m 5 cifras significativas 5,00 0 m 4 cifras significativas 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

12. Operaciones con cifras significativas Adición y sustracción Forma 1: 3 577,0 m + 1,2699 m + 13,455 m + 105,55 m 3 577,0 m + 1,3 m + 13,5 m + 105,6 m = 3 697,4 m Forma 2: 3 577,0 m + 1,2699 m + 13,455 m + 105,55 m = 3 697,3 m Efectuar las siguientes operaciones: 351 cm + 200,78 cm = 552 cm 351 cm + 200,8 cm = 552 cm 350,5 g - 200,78 g = 149,7 g 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

13. Operaciones con cifras significativas Multiplicación y división 11,2 cm x 6,7 cm = 75 cm 2 2 cifras significativas 1 600 m /58,0 s = 27,6 m/s 3 cifras significativas 12,50 m x 20,8 m = 260 m 2 3 cifras significativas 1 000,75 g/ 20,5 cm 3 = 48,8 g/cm 3 3 cifras significativas 12,75 m / 0,560 s 22,8 m/s 3 cifras significativas 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

14. Movimiento en una dimensión Movimiento en una dimensión: Definiciones generales, Movimiento con velocidad constante (MRU)

15. Movimiento rectilíneo Se denomina movimiento rectilíneo a aquel movimiento cuya trayectoria es una línea recta. Las magnitudes más importantes son: Posición inicial ( x i ) Posición final ( x f ) Tiempo transcurrido (D t ) Desplazamiento:  x Con estas magnitudes se define la tasa media de cambio de la posición: velocidad media 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

16. Ejercicios Ejercicio 1 . Un cometa que viaja directamente hacia el Sol, es detectado por primera vez en x i = 3,00·10 12 m respecto al Sol. Exactamente un año después se encuentra en x f = 2,10·10 12 m. Determine su desplazamiento y velocidad media. Solución Ejercicio 2. Un corredor recorre 100 m en 12,0 s; luego da la vuelta y recorre 50,0 m más en 30,0 s y en dirección al punto en que inició su movimiento. ¿cuál es la velocidad media para toda su trayectoria? Solución 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

17. Distancia recorrida (d) Es una magnitud escalar que representa la longitud de la trayectoria recorrida por el móvil. En el movimiento rectilíneo, la distancia recorrida coincide con el valor del desplazamiento sólo si el móvil no cambia de sentido. 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza 0 5,0 10,0 7,0

18. Solución Como  x = 0-(-3,0)m = 3,0 m Como d =15,0 m , Rapidez media (r) Rapidez media. Se define como la distancia recorrida ( d ) por el móvil en la unidad de tiempo. Ejercicio 3 . Observa el movimiento del deportista y determina su velocidad media y rapidez media si todo el movimiento se realiza en t = 3,0 s . 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza Velocidad media Rapidez media 0 -3,0 6,0

19. Ejercicio 4 Un vehículo parte de la posición -25,0 m de cierta esquina. Al cabo de 70,00 s se encuentra en la posición 245,0 m . ¿Cuál ha sido su velocidad si se sabe que se movió con velocidad constante? Solución x 1 = -25,0 m x 2 = 245,0 m t = 70,00 s Es aquel movimiento en el que la velocidad en cualquier instante permanece constante. Esto es, que se desplaza en línea recta, en una sola dirección y recorriendo intervalos iguales en tiempos iguales. Si se toma en cuenta que en este tipo de movimiento la velocidad es igual a la velocidad media, obtendremos la ecuación del MRU. Movimiento rectilíneo uniforme 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza

20. El gráfico posición-tiempo ( x-t ) se obtiene de tabular las posiciones para instantes definidos. Por ejemplo, si la velocidad del móvil es 5,0 m/s y parte de la posición inicial 2,0 m realizando un mru, la ecuación correspondiente es: La gráfica en los ejes x-t tiene el siguiente aspecto: Del gráfico puedes saber la posición inicial del móvil, la posición en cada instante y la velocidad. Gráfico posición-tiempo 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza t (m) x(m) 0 2,0 1 7,0 2 12,0 3 17,0 x (m) t (s) 2,0 7,0 12,0 17,0 1,0 2,0 3,0

21. Como en el MRU la velocidad es constante, la gráfica velocidad-tiempo será una recta horizontal, paralela al eje del tiempo. De este tipo de gráfico puedes obtener directamente el valor de la velocidad, v = +5,0 m/s . También puedes obtener el desplazamiento total del móvil, calculando el “área” comprendida entre el gráfico de la velocidad y el eje del tiempo.  x = v  t = (+5,0 m/s) (3,0 s) = +15,0 m Nota: Si la velocidad hubiera sido negativa, el área también lo sería y correspondería a un desplazamiento negativo. Observa que los valores obtenidos de  x y v coinciden en ambos gráficos al tratarse de un mismo caso. Gráfico velocidad-tiempo 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza v (m/s) t (s) 5,0 1,0 2,0 3,0

22. Semana 1 BALOTARIO DE EJERCICIOS

23. Balotario (EA) Conversión de unidades Página 16 44-49 50-58 Cinemática Página 44 48-63 06/09/09 Yuri Milachay, Eduardo Castillo, Adalberto Mestanza