Ecuaciones diferenciales de equivalencia 55555

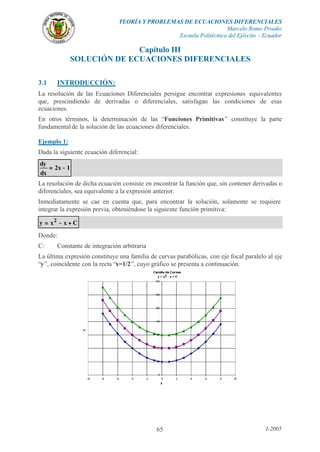
TEORÍA Y PROBLEMAS DE ECUACIONES DIFERENCIALES
Marcelo Romo Proaño
Escuela Politécnica del Ejército - Ecuador
I-200565
Capítulo III
SOLUCIÓN DE ECUACIONES DIFERENCIALES
3.1 INTRODUCCIÓN:
La resolución de las Ecuaciones Diferenciales persigue encontrar expresiones equivalentes
que, prescindiendo de derivadas o diferenciales, satisfagan las condiciones de esas
ecuaciones.
En otros términos, la determinación de las “Funciones Primitivas” constituye la parte
fundamentalde la solución de las ecuaciones diferenciales.
Ejemplo 1:
Dada la siguiente ecuación diferencial:
1x2
dx
dy
−=
La resolución de dicha ecuación consiste en encontrar la función que, sin contener derivadas o
diferenciales, sea equivalente a la expresión anterior.
Inmediatamente se cae en cuenta que, para encontrar la solución, solamente se requiere
integrar la expresión previa, obteniéndose la siguiente función primitiva:
Cxxy 2
+−=
Donde:
C: Constante de integración arbitraria
La última expresión constituye una familia de curvas parabólicas, con eje focal paralelo al eje
“y”, coincidente con la recta “x=1/2”, cuyo gráfico se presenta a continuación.

I-200566
La posición vertical del foco de cada parábola de la familia dibujada (también la posición
vertical del vértice de las curvas especificadas) depende del valor asignado a la constante
arbitraria de integración “C”.
La tabla que sirve de base para la generación del gráfico anterior se la puede elaborar en una
hoja electrónica con un contenido similar al siguiente:
En ocasiones, la solución de las ecuaciones diferenciales puede basarse en procesos de simple
integración como el que se presentó en el ejemplo previo; alternativamente se puede recurrir a
procesos de derivación; en otras circunstancias se pueden utilizar artificios matemáticos que
dependerán de la forma general de las ecuaciones, y en otras ocasiones se utilizarán
propiedades especiales de las ecuaciones diferenciales.
Cuando no es factible determinar las funciones primitivas correspondientes a una ecuación
diferencial, puede resultar conveniente la utilización de métodos numéricos que nos permitan
entender su comportamiento, e inclusive pueden favorecer la obtención de una representación
gráfica.
Problema Resuelto 1*:
Verificar si la función detallada a continuación es solución de la ecuación diferencial
planteada.
1e2y x3
+= Funciónsolución
3y3
dx
dy
−= Ecuación diferencial
Solución:
Calculando la primera derivada de la función solución:
x3
e6
dx
dy
=
Reemplazando la función solución y su derivada en la ecuación diferencial.

I-200567
3y3
dx
dy
−=
3)1e2(3)e6(
y
x3
dx
dy
x3
−+=
48476876
Simplificando:
3)3e6(e6 x3x3
−+=
33e6e6 x3x3
−+=
x3x3
e6e6 = Verificado
NOTA 1: Se ha verificado que la función es solución de la ecuación diferencial mediante
derivación de la función y reemplazo de la función y su derivada en la ecuación diferencial.
Al obtenerse una identidad se verifica la hipótesis del problema.
NOTA 2: Es importante notar que la función presentada no es la única solución de la
ecuación diferencial. Cualquier valor que preceda a la expresión exponencial “e3x
” cumplirá
con la ecuación diferencial, por lo que una solución general sería:
1e.Ay x3
+= Función solución general
Donde:
A: Constante arbitraria
Problema Resuelto 2:
planteada.
x2y = Funciónsolución

I-200568
x
y
2
dx
dy
= Ecuación diferencial
Solución:
2
dx
dy
=
Reemplazando la función solución y su derivada en la ecuación diferencial:
x
y
2
dx
dy
=
}
}
x
)x2(
2)2(
y
dx
dy
=
Simplificando:
42 =
42 ≠ No se verifica
NOTA: La función presentada no es solución de la ecuación diferencial propuesta.
planteada.
2
xy = Funciónsolución
x
y
2
dx
dy
Solución:
x2
dx
dy
=
Reemplazando la función solución y su derivada en la ecuación diferencial:
x
y
2
dx
dy
=
x
)x(
2)x2(
2
=
Simplificando:
x2x2 = Verificado

I-200569
NOTA: La función presentada no es la única solución de la ecuación diferencial. La siguiente
es la solución general:
2
x.Ay = Función solución general
Donde:
planteada.
1xy −= Funciónsolución
1x
y
dx
dy
−
Solución:
1
dx
dy
=
Reemplazando la función solución y su derivada en la ecuación diferencial.
1x
y
dx
dy
−
=
}
1x
)1x(
)1(
y
dx
dy
−
−
=
876
Simplificando:

I-200570
11 = Verificado
NOTA: La función presentada no es la única que es solución de la ecuación diferencial. La
siguiente es la solución general:
)1x(Ay −= Función solución general
Donde:
3.2 MÉTODO DE SEPARACIÓN DE VARIABLES:
Consiste en colocar, en expresiones separadas de la ecuación diferencial, las funciones de
cada variable con su respectivo diferencial y proceder a la integración. Los detalles
característicos de la ecuación diferencial son los que definen los mecanismos para lograr la
separación de las variables.
Resolver la siguiente ecuación diferencial y representarla gráficamente:
01xx6x3y 23
=−−+−′
Solución:
Despejando la primera derivada de “y”:
1xx6x3y 23
++−=′
La derivada se puede expresar como:
dx
dy
y =′
Reemplazando:

I-200571
1xx6x3
dx
dy 23
++−=
Separando las diferenciales del miembro izquierdo:
dx)1xx6x3(dy 23
++−=
Integrando ambos miembros:
∫∫ ++−= dx)1xx6x3(dy 23
Ejecutando las integrales:
Cxx
2
1
x
3
6
x
4
3
y 234
+++−=
Simplificando:
Cxx
2
1
x2x
4
3
y 234
+++−= Solución
Donde:
La hoja electrónica que permite graficar la función puede ser la siguiente:

I-200572
Verificación:
El punto de partida es la función solución:
Cxx
2
1
x2x
4
3
y 234
+++−=
La derivada de “y” respecto a “x” es:
1x
2
2
x6x
4
12
y 23
++−=′
Simplificando:
1xx6x3y 23
++−=′
La ecuación diferencial original es:
01xx6x3y 23
=−−+−′
Reemplazando la derivada “y′ ” en la ecuación diferencial se tiene:
01xx6x3)1xx6x3( 23
y
23
=−−+−++−
′
444 8444 76
Simplificando:
00 = Verificado
NOTA 1: Se ha conseguido resolver la ecuación diferencial mediante su transformación en
un proceso de integración. Para el efecto se han realizados manejos algébricos que permiten la
separación de las variables y de sus diferenciales.
NOTA 2: La presencia de la constante de integración arbitraria dentro de la solución de la
ecuación diferencial da lugar a una familia de curvas que cumplen con la ecuación diferencial.
0e2y x3
=−′

I-200573
Solución:
Despejando la primera derivada de “y”:
x3
e2y =′
La derivada se puede expresar como:
dx
dy
y =′
x3
e2
dx
dy
=
dxe2dy x3
=
∫∫ = dxe2dy x3
Ce
3
2
y x3
+= Solución
Donde:
La hoja electrónica que dio origen al gráfico es:

I-200574
Verificación:
La función solución es:
Ce
3
2
y x3
+=
La derivada de “y” respecto a “x” es:
x3
e
3
6
y =′
Simplificando:
x3
e2y =′
0e2y x3
=−′
Reemplazando la derivada “y′ ” en la ecuación diferencial se tiene:
0e2)e2( x3
y
x3
=−
′
876
Simplificando:
00 = Verificado
Resolver la siguiente ecuación diferencial:
05x3x4y 2
=−−+′′
Solución:
Despejando la segunda derivada de “y”:
5x3x4y 2
++−=′′

I-200575
La segunda derivada normalmente se la expresa como:
2
2
dx
yd
y =′′
Pero la segunda derivada es también “la derivada de la primera derivada”:
dx
yd
y
′
=′′
Reemplazando:
5x3x4
dx
yd 2
++−=
′
dx)5x3x4(yd 2
++−=′
∫∫ ++−=′ dx)5x3x4(yd 2
1
23
Cx5x
2
3
x
3
4
y +++−=′
Reemplazando “y′ ” por su expresión equivalente:
dx
dy
y =′
1
23
Cx5x
2
3
x
3
4
dx
dy
+++−=
Separando las diferenciales:
dxCx5x
2
3
x
3
4
dy 1
23






+++−=
∫∫ 





+++−= dxCx5x
2
3
x
3
4
dy 1
23
21
234
CxCx
2
5
x
6
3
x
12
4
y ++++−=
Simplificando:
21
234
CxCx
2
5
x
2
1
x
3
1
y ++++−= Solución

I-200576
Donde:
C1: Constante de integración arbitraria
Verificación:
21
234
CxCx
2
5
x
2
1
x
3
1
y ++++−=
La primera derivada de “y” respecto a “x” es:
1
23
Cx
2
10
x
2
3
x
3
4
y +++−=′
Simplificando:
1
23
Cx5x
2
3
x
3
4
y +++−=′
La segunda derivada de “y” es:
5x
2
6
x
3
12
y 2
++−=′′
Simplificando:
5x3x4y 2
++−=′′
05x3x4y 2
=−−+′′
Reemplazando la segunda derivada “y″ ” en la ecuación diferencial y simplificando se tiene:
05x3x4)5x3x4( 2
y
2
=−−+++−
′′
44 844 76
Simplificando:
00 = Verificado
NOTA 1: La resolución de la ecuación diferencial de segundo orden ha sido transformada en
un doble proceso de integración, lo que produjo 2 constantes de integración arbitrarias. La
verificación se efectuó mediante un doble proceso de derivación.
NOTA 2: Con el objeto de facilitar la realización de las 2 integraciones requeridas,
ejecutándolas de manera separada, la segunda derivada se expresó como “la derivada de la
primera derivada”.

I-200577
05x2x3y 2
=+−+′′
Solución:
Despejando la segunda derivada:
5x2x3y 2
−+−=′′
La segunda derivada es la derivada de la primera derivada de la función:
dx
yd
y
′
=′′
5x2x3
dx
yd 2
−+−=
′
dx)5x2x3(yd 2
−+−=′
∫∫ −+−=′ dx)5x2x3(yd 2
1
23
Cx5x
2
2
x
3
3
y +−+−=′
Simplificando:
1
23
Cx5xxy +−+−=′
Reemplazando “y′ ” por las diferenciales correspondientes:
1
23
Cx5xx
dx
dy
+−+−=
dx)Cx5xx(dy 1
23
+−+−=
∫∫ +−+−= dx)Cx5xx(dy 1
23
21
234
CxCx
2
5
x
3
1
x
4
1
y ++−+−= Solución
Donde:

I-200578
Verificación:
21
234
CxCx
2
5
x
3
1
x
4
1
y ++−+−=
1
23
Cx
2
10
x
3
3
x
4
4
y +−+−=′
Simplificando:
1
23
Cx5xxy +−+−=′
5x2x3y 2
−+−=′′
05x2x3y 2
=+−+′′
Reemplazando la segunda derivada “y″ ” en la ecuación diferencial se tiene:
05x2x3)5x2x3( 2
y
2
=+−+−+−
′′
44 844 76
Simplificando:
00 = Verificado
07)x2(Cos3y2 =−+′′
Solución:
7)x2(Cos3y2 +−=′′
2
7
)x2(Cos
2
3
y +−=′′
La segunda derivada es la derivada de la primera derivada:
dx
yd
y
′
=′′
2
7
)x2(Cos
2
3
dx
yd
+−=
′

I-200579
dx
2
7
)x2(Cos
2
3
yd 





+−=′
∫∫ 





+−=′ dx
2
7
)x2(Cos
2
3
yd
1Cx
2
7
)x2(Sen
4
3
y ++−=′
dx
dy
y =′
1Cx
2
7
)x2(Sen
4
3
dx
dy
++−=
dxCx
2
7
)x2(Sen
4
3
dy 1 





++−=
∫∫ 





++−= dxCx
2
7
)x2(Sen
4
3
dy 1
21
2
CxCx
4
7
)x2(Cos
8
3
y +++= Solución
Donde:
Verificación:
21
2
CxCx
4
7
)x2(Cos
8
3
y +++=
1Cx
4
14
)x2(Sen
8
6
y ++−=′
Simplificando:
1Cx
2
7
)x2(Sen
4
3
y ++−=′

I-200580
La segunda derivada de “y” respecto a “x” es:
2
7
)x2(Cos
4
6
y +−=′′
Simplificando:
2
7
)x2(Cos
2
3
y +−=′′
07)x2(Cos3y2 =−+′′
07)x2(Cos3
2
7
)x2(Cos
2
3
2
y
=−+





+−
′′
444 8444 76
Simplificando:
07)x2(Cos3
2
14
)x2(Cos
2
6
=−+





+−
[ ] 07)x2(Cos37)x2(Cos3 =−++−
00 = Verificado
0)t3(Seny =−′′
Solución:
)t3(Seny =′′
Por la forma de las expresiones que aparecen en la ecuación diferencial, “y″ ” es la segunda
derivada de “y” respecto a “t” (no es la segunda derivada de “y” respecto a “x”).
2
2
dt
yd
y =′′
Pero la segunda derivada es también la derivada de la primera derivada:
dt
yd
y
′
=′′
Reemplazando se tiene:
)t3(Sen
dt
yd
=
′

I-200581
dt)t3(Senyd =′
dt)t3(Senyd ∫∫ =′
1C)t3(Cos
3
1
y +−=′
dt
dy
y =′
1C)t3(Cos
3
1
dt
dy
+−=
dtC)t3(Cos
3
1
dy 1 





+−=
∫∫ 





+−= dtC)t3(Cos
3
1
dy 1
21 CtC)t3(Sen
9
1
y ++−= Solución
Donde:

I-200582
NOTA: Las curvas obtenidas son sinusoides que se desarrollan sobre ejes de referencia
correspondientes a rectas en diferentes partes del plano y con inclinaciones diferentes. La
posición y orientación del eje de referencia depende de los valores de las constantes “C1” y
“C2”
La tabla que dio origen al gráfico es:
Verificación:
21 CtC)t3(Sen
9
1
y ++−=
La primera derivada de “y” respecto a “t” es:
1C)t3(Cos
9
3
y +−=′
Simplificando:
1C)t3(Cos
3
1
y +−=′
La segunda derivada de “y” respecto a “t” es:
)t3(Sen
3
3
y =′′
Simplificando:
)t3(Seny =′′
0)t3(Seny =−′′

I-200583
0)t3(Sen)t3(Sen
y
=−
′′
48476
Simplificando:
00 = Verificado
03x12ey x
=−++′′′ −
Solución:
Despejando la tercera derivada de “y”:
3x12ey x
+−−=′′′ −
La tercera derivada es la derivada de la segunda derivada:
dx
yd
y
′′
=′′′
Reemplazando:
3x12e
dx
yd x
+−−=
′′ −
dx)3x12e(yd x
+−−=′′ −
∫∫ +−−=′′ −
dx)3x12e(yd x
1
2x
Cx3x
2
12
ey ++−=′′ −
Simplificando:
1
2x
Cx3x6ey ++−=′′ −
La segunda derivada es la derivada de la primera derivada:
dx
yd
y
′
=′′
Reemplazando:
1
2x
Cx3x6e
dx
yd
++−=
′ −

I-200584
dx)Cx3x6e(yd 1
2x
++−=′ −
∫∫ ++−=′ −
dx)Cx3x6e(yd 1
2x
21
23x
CxCx
2
3
x
3
6
ey +++−−=′ −
Simplificando:
21
23x
CxCx
2
3
x2ey +++−−=′ −
dx
dy
y =′
21
23x
CxCx
2
3
x2e
dx
dy
+++−−= −
dxCxCx
2
3
x2edy 21
23x






+++−−=
−
∫∫ 





+++−−=
−
dxCxCx
2
3
x2edy 21
23x
32
2134x
CxCx
2
C
x
6
3
x
4
2
ey ++++−= −
Simplificando:
32
2134x
CxCx
2
C
x
2
1
x
2
1
ey ++++−= −
Solución
Donde:
Verificación:

I-200585
32
2134x
CxCx
2
C
x
2
1
x
2
1
ey ++++−= −
2
123x
Cx
2
C2
x
2
3
x
2
4
ey +++−−=′ −
Simplificando:
21
23x
CxCx
2
3
x2ey +++−−=′ −
1
2x
Cx
2
6
x6ey ++−=′′ −
Simplificando:
1
2x
Cx3x6ey ++−=′′ −
La tercera derivada de “y” es:
3x12ey x
+−−=′′′ −
03x12ey x
=−++′′′ −
Reemplazando la tercera derivada “y″′ ” en la ecuación diferencial se tiene:
03x12e)3x12e( x
y
x
=−+++−− −
′′′
−
44 844 76
00 = Verificado
NOTA 1: La solución a la ecuación diferencial es una familia de parábolas de cuarto grado
más una “función exponencial amortiguada” (exponente con signo negativo) para los
valores positivos de “x”.
NOTA 2: La resolución de la ecuación diferencial de tercer orden ha sido transformada en un
triple proceso de integración, lo que produjo 3 constantes de integración arbitrarias. La
verificación se efectuó mediante un triple proceso de derivación.
NOTA 3: Para facilitar la realización de las 3 integrales requeridas en la resolución de la
ecuación diferencial, ejecutándolas por separado, la tercera derivada se expresó como “la
derivada de la segunda derivada”, y la segunda derivada se describió como la “derivada de
la primera derivada”.

I-200586
y
x
dx
dy
=
Solución:
Separamos todas las expresiones en “x” de las expresiones en “y”:
dx.xdy.y =
∫∫ = dx.xdy.y
C
2
x
2
y 22
+=
Agrupando las variables en un solo miembro:
C
2
x
2
y 22
=−
Multiplicando por “2”:
C2xy 22
=−
Reemplazando “2C” por una nueva constante “k”:
kxy 22
=− Solución
NOTA: Cuando “k” tiene valor positivo, la solución es la ecuación de una familia de
hipérbolas con centro en el origen de coordenadas y eje focal coincidente con el eje de las
“x”. Si el valor de “k” es negativo la solución es también una familia de hipérbolas con centro
en el origen de coordenadas, pero el eje focal coincide con el eje de las “y”.

I-200587
NOTA: En ambas circunstancias estamos hablando de una relación y no de una función, pues
en el primer caso para cada valor de “x” existen 2 valores de “y” (dos puntos, en dos
segmentos de curva), y en el segundo caso para cada valor de “y” existen 2 valores de “x”.
Verificación:
La solución es:
kxy 22
=−
Obteniendo diferenciales en la expresión (las reglas de diferenciación son similares a las de
derivación):
0dx.x2dy.y2 =−
dx.x2dy.y2 =
Simplificando:
dx.xdy.y =
Reagrupando las diferenciales en forma de derivadas:
y
x
dx
dy
= Verificado
NOTA: A diferencia de los problemas anteriores en que la ecuación diferencial solo contenía
una de las derivadas de la variable dependiente, pero no la variable “y”, en el presente caso,
debido a la presencia simultánea de “y”, “y′ ” y alguna función de la variable independiente
“x”, la verificación ha consistido en recuperar la ecuación diferencial original en base a su
solución matemática.

I-200588
x
y
dx
dy
=
Solución:
x
dx
y
dy
=
∫∫ =
x
dx
y
dy
Ejecutando las integrales, que claramente conducen a expresiones logarítmicas por presentar
en el numerador de las fracciones las derivadas (propiamente las diferenciales) de los
correspondientes denominadores:
C)xln()yln( +=
Por facilidad de simplificación posterior se reemplaza la constante “C” por el logaritmo
natural de otra constante (“k”), de modo que todas las expresiones sean funciones
logarítmicas.
)kln()xln()yln( +=
La suma de logaritmos es el logaritmo de un producto:
)x.kln()yln( =
Aplicando el antilogaritmo natural a ambos miembros:
x.ky = Solución
NOTA 1: Debido a que los procesos de integración condujeron solamente a expresiones
logarítmicas, resultó conveniente reemplazar la constante de integración por el logaritmo de
otra constante, pues permitió una simplificación importante de la expresión final de la
solución.
NOTA 2: La solución (la función primitiva) es la ecuación de una familia de rectas que pasan
por el origen y tienen una pendiente variable “k” (en Geometría Analítica la ecuación de esa
familia de rectas se escribe “y=m.x”).

I-200589
Verificación:
La solución es:
x.ky =
Obteniendo la derivada de “y” respecto a “x”:
k
dx
dy
=
En la función solución se despeja “k”:
x
y
k =
Dos cosas iguales a una tercera son iguales entre sí:
x
y
dx
dy
= Verificado
NOTA 1: Mientras mayor sea la complejidad de la ecuación diferencial, más artificiosa se
puede volver la verificación.
NOTA 2: En todos los casos en que aparecen variables y sus derivadas se toma como punto
de partida la solución obtenida y como punto de llegada la ecuación diferencial original.
2
2
y
x1
dx
dy −
=
Solución:

I-200590
dx)x1(dy.y 22
−=
∫∫ −= dx).x1(dy.y 22
C
3
x
x
3
y 33
+−=
C3xx3y 33
+−=
0C3x3yx 33
=−−+
Reemplazando “-3C” por otra constante (“k”):
0kx3yx 33
=+−+ Solución
Donde:
k: Constante arbitraria
NOTA 1: En muchos casos es conveniente el reemplazo de constantes de integración por
otras expresiones también constantes para simplificar las expresiones.
NOTA 2: La hoja electrónica es especialmente útil para encontrar valores para las constantes
involucradas, de modo que los gráficos de las funciones sean representativos de la solución.
Verificación:
La solución es:
0kx3yx 33
=+−+
Derivando respecto a “x” se tiene:

I-200591
03
dx
dy
.y3x3 22
=−+
Simplificando:
01
dx
dy
.yx 22
=−+
Despejando la derivada:
22
x1
dx
dy
.y −=
Despejando la derivada:
2
2
y
x1
dx
dy −
= Verificado
)x(Tan).y(Sec
dx
dy
=
Solución:
Separando las variables:
dx).x(Tan
)y(Sec
dy
=
Colocando las funciones trigonométricas en Senos y Cosenos:
dx
)x(Cos
)x(Sen
dy).y(Cos ⋅=
Integrando:
∫∫ ⋅= dx
)x(Cos
)x(Sen
dy).y(Cos
[ ] C)x(Cosln)y(Sen +−=
[ ] C)x(Cosln)y(Sen =+ Solución
Donde:
C: Constante arbitraria de integración

I-200592
NOTA 1: La solución a la ecuación diferencial es una expresión periódica que tiene valores
dentro del campo de los reales en ciertos intervalos y carece de soluciones en otros intervalos.
Los intervalos en que no existe solución corresponden a aquellos valores en que el Coseno de
“x” adquiere valores negativos y por consiguiente no es factible obtener su logaritmo, lo que
se refleja en la hoja electrónica que se utiliza para generar los gráficos.
NOTA 2: Debido a la presencia de funciones Seno y Coseno, cuyos valores fluctúan entre “-
1” y “+1”, no existe solución real para todos los valores de “C”, pues cuando “C≤-3” o
“C≥+1” no existen valores reales que cumplan con la “Función Primitiva”.
Verificación:
La solución es:
[ ] C)x(Cosln)y(Sen =+
Obteniendo diferenciales de la expresión:
0dx
)x(Cos
)x(Sen
dy).y(Cos =⋅
−
+

I-200593
Simplificando:
0dx
)x(Cos
)x(Sen
dy).y(Cos =⋅−
Pero la expresión “Sen(x)/Cos(x)” es igual a “Tan(x)”:
0dx).x(Tandy).y(Cos =−
dx).x(Tandy).y(Cos =
Agrupando las diferenciales:
)y(Cos
)x(Tan
dx
dy
=
Reemplazando “Cos(y)” por el inverso de “Sec(y)”:
)x(Tan).y(Sec
dx
dy
= Verificado
NOTA: Generalmente los pasos seguidos en la resolución de la ecuación diferencial dan la
pauta de los artificios requeridos para su verificación.
3.3 FACTORES Y DIVISORES DE INTEGRACIÓN:
Existen determinadas expresiones algébricas que al multiplicar o dividir a las ecuaciones
diferenciales las simplifican pues facilitan la separación de variables y posibilitan su
integración; tales factores o divisores se denominan factores o divisores de integración, de
acuerdo al caso.
0dy)yxy(dx)xyx4( 22
=+++
Solución:
Factorando la ecuación diferencial para facilitar la separación de variables:
0dy)x1(ydx)y4(x 22
=+++
Dividiendo para el producto “(4+y2
).(1+x2
)” constituido por las expresiones que impiden la
integración directa de los 2 términos de la ecuación diferencial, que es el “divisor de
integración”. El inverso de la expresión es el “factor de integración”.
0
)x1).(y4(
dy)x1(ydx)y4(x
22
22
=
++
+++
0
)x1).(y4(
dy)x1(y
)x1).(y4(
dx)y4(x
22
2
22
2
=
++
+
+
++
+

I-200594
Simplificando:
0
y4
dy.y
x1
dx.x
22
=
+
+
+
Integrando:
C
y4
dy.y
x1
dx.x
22
=
+
+
+
∫∫
C)y4ln(
2
1
)x1ln(
2
1 22
=+++
C2)y4ln()x1ln( 22
=+++
Reemplazando “2C” por el logaritmo natural de “k”:
)kln()y4ln()x1ln( 22
=+++
El logaritmo del producto es la suma de logaritmos:
{ } )kln()y4).(x1(ln 22
=++
Aplicando el antilogaritmo a ambos miembros:
k)y4).(x1( 22
=++ Solución
Donde:
k: Constante arbitraria de integración
Verificación:
La solución es:

I-200595
k)y4).(x1( 22
=++
Obteniendo diferenciales de la expresión anterior:
0dx).x2).(y4(dy).y2).(x1( 22
=+++
Simplificando:
0dx).y4(xdy).x1(y 22
=+++
Efectuando los productos:
0dx).xyx4(dy).yxy( 22
=+++
Reordenando:
0dy)yxy(dx)xyx4( 22
=+++ Verificado
dy.xdx.ydy.x4 2
=−
Solución:
dx.ydy.xdy.x4 2
=−
dx.ydy).xx4( 2
=−
Dividiendo para el producto “(4x-x2
).y”, que es el “divisor de integración”:
y).xx4(
dx.y
y).xx4(
dy).xx4(
22
2
−
=
−
−
Simplificando:
2
xx4
dx
y
dy
−
=
)x4(x
dx
y
dy
−
=
Descomponiendo el miembro derecho en fracciones parciales y reemplazando:
x4
B
x
A
)x4(x
1
−
+=
−
Obteniendo denominador común en el miembro derecho:
)x4(x
x.B)x4(A
)x4(x
1
−
+−
=
−
Destruyendo paréntesis en el numerador:

I-200596
)x4(x
x.BAxA4
)x4(x
1
−
+−
=
−
Agrupando:
)x4(x
A4)AB(x
)x4(x
1
−
+−
=
−
Convirtiendo al numerador de la fracción izquierda en un polinomio similar al del
numerador derecho.
)x4(x
A4x)AB(
)x4(x
1x.0
−
+−
=
−
+
De donde, al igualar los polinomios de los numeradores de las 2 fracciones se tiene:
1A4
0AB
=
=−
Resolviendo el sistema de ecuaciones se tiene:
4/1A =
4/1B =
La fracción original es equivalente a:
x4
4/1
x
4/1
)x4(x
1
−
+=
−
x4
dx
4
1
x
dx
4
1
y
dy
−
+=
x4
dx
x
dx
y
dy.4
−
+=
4x
dx
x
dx
y
dy.4
−
−=
Integrando:
∫∫∫ −
−=
4x
dx
x
dx
y
dy.4
C)4xln()xln()yln(.4 +−−=
Reemplazando “C” por el “ln(k)”:
)kln()4xln()xln()yln(.4 +−−=
Agrupando los logaritmos:






−
=
4x
x.k
ln)yln(
4
Calculando los antilogaritmos:

I-200597
4x
x.k
y4
−
= Solución
Donde:
0dy)yxyx2(dx)xyyx3( 43232
=++−
Solución:
Factorando la ecuación diferencial para facilitar la separación de variables:
0dy)yy2(xdx)xx3(y 4232
=++−
Dividiendo para el producto “x3
.y”, que es el “divisor de integración”:
0
y.x
dy)yy2(xdx)xx3(y
3
4232
=
++−
0
y.x
dy)yy2(x
y.x
dx)xx3(y
3
423
3
2
=
+
+
−
Simplificando:
0
y
dy)yy2(
x
dx)xx3( 42
3
2
=
+
+
−
0dy)yy2(
x
dx)1x3( 3
2
=++
−
Separando los componentes de la integración y simplificando:
0dy.ydy.y2
x
dx
x
dx.x3 3
22
=++−

I-200598
0dy.ydy.y2dx.x
x
dx3 32
=++− −
Integrando:
Cdy.ydy.y2dx.x
x
dx.3 32
=++− ∫∫∫∫
−
C
4
y
2
y2
1
x
)xln(.3
421
=++
−
−
−
Simplificando:
C
4
y
yx)xln(.3
4
21
=+++ −
C
4
y
y
x
1
)xln(.3
4
2
=+++ Solución
Donde:
NOTA: Para graficar la solución podría resultar conveniente representarla como una ecuación
de segundo grado en que la variable independiente es “y2
”, que puede ser representada como
una nueva variable “z”.
Reordenando la expresión:
C
x
1
)xln(.3y
4
y 2
4
=+++
0C
x
1
)xln(.3y
4
y 2
4
=−+++
Reemplazando la constante “-C” por una constante “k”:
0k
x
1
)xln(.3y
4
y 2
4
=++++
Agrupando el término independiente de “y2
”:
0k
x
1
)xln(.3y
4
y 2
4
=





++++
0k
x
1
)xln(.3.4y4y
24
=





++++
Poniendo la expresión en función de “y2
”:
[ ] [ ] 0k
x
1
)xln(.3.4y4y
222
=





++++
Para simplificar el procedimiento puede utilizarse la siguiente ecuación paramétrica:
2
yz = o zy ±= Ecuación paramétrica para graficación
Reemplazando la ecuación paramétrica en la expresión previa:

I-200599
0k
x
1
)xln(.3.4z4z
2
=





++++
Resolviendo la ecuación de segundo grado para la variable “z” se tiene:
)1(2
k
x
1
)xln(.3.4)1(444
z
2












++−±−
=
Simplificando:
2
k
x
1
)xln(.316164
z






++−±−
=
2
k
x
1
)xln(.31164
z












++−±−
=
Extrayendo el “16” de la expresión radical:
2
k
x
1
)xln(.3144
z






++−±−
=
2
k
x
1
)xln(.3144
z
−−−±−
=
Simplificando:
k
x
1
)xln(.3122z −−−±−=
Reemplazando “z” en función de “y”:
2
yz =
k
x
1
)xln(.3122y2
−−−±−=
Despejando “y”:
k
x
1
)xln(.3122y −−−±−±=
Para el valor negativo del radical interior no existen valores dentro del conjunto de
los números reales por lo que la expresión para la graficación es:
k
x
1
)xln(.3122y −−−+−±= Solución para graficación
Un aspecto que es importante mencionar es que no siempre se podrá obtener con facilidad una
representación gráfica de las funciones equivalentes a las ecuaciones diferenciales y
condiciones de frontera planteadas.

I-2005100
0dy).1x(ydx).1y(x 22
=−++
Solución:
Dividiendo para “(y+1).(x-1)”, que son los factores que impiden la integración directa:
0
)1x).(1y(
dy).1x(ydx).1y(x 22
=
−+
−++
0
)1x).(1y(
dy).1x(y
)1x).(1y(
dx).1y(x 22
=
−+
−
+
−+
+
Simplificando:
0
1y
dy.y
1x
dx.x 22
=
+
+
−
Separando la parte entera (divisible) de la parte no divisible en las 2 fracciones:
La determinación de la parte entera polinómica y la parte fraccionaria polinómica se
puede realizar mediante una sencilla división, en la que el cociente es la parte entera
y el residuo dividido para el divisor es la parte fraccionaria no divisible.
)x(D )x(d
.............. )x(Q
)x(R
)x(d
)x(R
)x(Q
)x(d
)x(D
+=

I-2005101
1x
1
1x
1x
x2
−
++=
−
2
x 1x −
+− xx2
1x +
+ x
+− 1x
+ 1
1y
1
1y
1y
y2
+
+−=
+
2
y 1y +
−− yy2
1y −
− y
++ 1y
+ 1
Reemplazando las equivalencias se tiene:
0dy.
1y
1
1ydx.
1x
1
1x =





+
+−+





−
++
Separando los componentes de la integración y simplificando:
0
1y
dy
dy).1y(
1x
dx
dx).1x( =
+
+−+
−
++
Integrando:
C
1y
dy
dy).1y(
1x
dx
dx).1x( =
+
+−+
−
++ ∫∫∫∫
C)1yln(y
2
y
)1xln(x
2
x 22
=++−+−++ Solución
Donde:
NOTA: Cuando es difícil o imposible despejar una de las variables, de modo que se pueda
construir la representación gráfica de una función (como en la expresión anterior), la hoja
electrónica se puede organizar de tal manera que por tanteos convergentes se llegue a una
aproximación aceptable de evaluación (que la evaluación del miembro izquierdo sea muy
parecida a la evaluación del miembro derecho).

I-2005102
La tabla a través de la cual se pudo construir el gráfico anterior es:
Para cada valor de “x” se asignan diferentes valores de “y”, de modo que en las columnas
“C”, “E” y “G” se evalúa el miembro izquierda de la ecuación y se procura que alcance un
valor que se aproxime mucho a “200”, “500” y “1000”.
)3y(x
y4
dx
dy
−
=
Solución:
dx.y4dy).3y(x =−
Dividiendo para “x.y”, que son los factores que impiden la integración directa:

I-2005103
y.x
dx.y4
y.x
dy).3y(x
=
−
Simplificando:
x
dx4
y
dy).3y(
=
−
Separando los componentes del miembro izquierdo:
x
dx4
y
dy.3
y
dy.y
=−
x
dx4
y
dy.3
dy =−
Integrando:
∫∫∫ =−
x
dx4
y
dy.3
dy
C)xln(.4)yln(.3y +=−
)kln()xln(.4)yln(.3y +=−
)x.kln(.4)yln(.3y =− Solución
Donde:
NOTA: La solución podría tener una expresión exponencial alternativa que eventualmente
podría favorecer su representación gráfica.
Introduciendo el valor “3” y el “4” como exponentes de las expresiones logarítmicas:
43
)x.kln()yln(y =−
)x.kln()yln(y 443
=−
Reemplazando la constante por otra más simple:
)x.kln()yln(y 4
1
3
=−
Agrupando las expresiones logarítmicas:
)x.kln()yln(y 4
1
3
+=
El logaritmo de un producto es la suma de los logaritmos:
)y.x.kln(y 34
1=
La expresión exponencial equivalente es:
34
1
y
y.x.ke =
De esta expresión se podría despejar “x” y obtener una expresión de esa variable en
función de “y”, lo que facilitaría la graficación.

I-2005104
3
1
y
4
y.k
e
x =
La expresión que se puede utilizar para crear gráficos sería:
4
3
1
y
y.k
e
x ±=
Esta expresión tiene 2 soluciones dentro del campo de los reales (cuando el
argumento del radical es positivo) y 2 soluciones en el campo de los números
complejos (cuando el argumento es negativo).
0dy).x1(dx.y.x 2
=++
Solución:
Dividiendo para “y.(1+x2
)”, que son los factores que impiden la integración directa:
0
)x1.(y
dy).x1(dx.y.x
2
2
=
+
++
Separando en 2 fracciones:
0
)x1.(y
dy).x1(
)x1.(y
dx.y.x
2
2
2
=
+
+
+
+
Simplificando:
0
y
dy
)x1(
dx.x
2
=+
+
Integrando:

I-2005105
0
y
dy
)x1(
dx.x
2
=+
+
∫∫
C)yln()x1ln(
2
1 2
=++
Multiplicando por “2” y simplificando:
C2)yln(.2)x1ln( 2
=++
C2)yln()x1ln( 22
=++
Reemplazando “2C” por el “ln(k)”:
)kln()yln()x1ln( 22
=++
( ) )kln()x1.(yln 22
=+
Aplicando antilogaritmos:
k)x1.(y 22
=+ Solución
Donde:
0d.d).(Ctg =θρ+ρθ
Solución:
Dividiendo para “ρ.Ctg(θ)”:

I-2005106
0
)(Ctg.
d.d).(Ctg
=
θρ
θρ+ρθ
0
)(Ctg.
d.
)(Ctg.
d).(Ctg
=
θρ
θρ
+
θρ
ρθ
Simplificando:
0
)(Ctg
dd
=
θ
θ
+
ρ
ρ
Pasando la función trigonométrica al numerador:
0d).(Tan
d
=θθ+
ρ
ρ
Integrando:
Cd).(Tan
d
=θθ+
ρ
ρ
∫∫
[ ] C)(Cosln)ln( =θ−ρ
[ ] )kln()(Cosln)ln( =θ−ρ
Pasando el logaritmo con signo negativo al miembro derecho:
[ ])(Cosln)kln()ln( θ+=ρ
[ ])(Cos.kln)ln( θ=ρ
)(Cos.k θ=ρ Solución
Donde:

I-2005107
3.4 CAMBIO DE VARIABLES:
Un artificio empleado con bastante frecuencia en ecuaciones diferenciales es el cambio de
variables, que significa la introducción de una o varias nuevas variables en función de las
variables ya existentes, lo que permite la eliminación de una o algunas de las variables
primarias y la simplificación de la ecuación diferencial original.
El tipo de expresiones que se utilizan en el cambio de variables depende de la forma general
de las ecuaciones planteadas.
Son usuales las nuevas variables que se obtienen a partir de operaciones básicas que afectan a
las variables originales, a constantes específicas, o a las derivadas de las funciones
involucradas en la ecuación diferencial.
3.4.1 Ecuaciones Diferenciales con Funciones Homogéneas:
Cuando se dispone de ecuaciones diferenciales con funciones homogéneas del mismo orden
para las 2 diferenciales, es conveniente introducir una nueva variable tal que una de las 2
variables iniciales sea igual a la nueva variable multiplicada por la otra variable inicial.
0dy.xy2dx).yx( 22
=−+
Solución:
Debido a que las potencias o las sumas de potencias de todos los componentes dan “2” (“x2
”,
“y2
”, “x.y”), la ecuación está conformada por funciones homogéneas de grado “2”, por lo que
puede ser resuelta mediante sustitución de variables.
La expresión para la sustitución de variables sería:
x.vy = Ecuación de cambio de variable
La expresión diferencial correspondiente es:

I-2005108
dv.xdx.vdy +=
Reemplazando en la ecuación diferencial original se tiene:
( ) 0)dv.xdx.v).(x.v(x2dx.)x.v(x 22
=+−+
Resolviendo:
0)dv.xdx.v.(v.x2dx).v1.(x 222
=+−+
Factorando “x2
”:
( ) 0)dv.xdx.v.(v2dx).v1(x 22
=+−+
Simplificando:
0)dv.xdx.v.(v2dx).v1( 2
=+−+
0dv.x.v2dx.v2dx).v1( 22
=−−+
0dv.x.v2dx).v1( 2
=−−
Dividiendo para el divisor de integración se tiene:
0
x).v1(
dv.x.v2dx).v1(
2
2
=
−
−−
Simplificando:
0
x).v1(
dv.x.v2
x).v1(
dx).v1(
22
2
=
−
−
−
−
0
)v1(
dv.v2
x
dx
2
=
−
−
C
)v1(
dv.v2
x
dx
2
=
−
− ∫∫
C
)v1(
dv.v2
x
dx
2
=
−
−
+ ∫∫
Ejecutando las integrales, que son del tipo logarítmico:
C)v1ln()xln( 2
=−+
Reemplazando la constante “C” por “ln(k)”:
)kln()v1ln()xln( 2
=−+

I-2005109
{ } )kln()v1.(xln 2
=−
Calculando el antilogaritmo:
k)v1.(x 2
=− Solución intermedia
Reemplazando “v” en función de “x” y “y”:
x
y
v =
k
x
y
1.x
2
=














− Solución
Donde:
Para la representación gráfica es preferible utilizar la expresión en que “y” aparece despejada:
x.kxy 2
−±=
NOTA 1: Debido a la forma general de la ecuación diferencial original, que tiene factores
“x2
+y2
” y “x.y”, la “Ecuación de Cambio de Variable” podría ser indistintamente “y=v.x” o
“x=v.y”.
NOTA 2: Generalizando, las ecuaciones con funciones homogéneas en “x” y “y” pueden ser
resueltas mediante cambios de variable de la forma “y=v.x” o “x=v.y”.
0dy.y.x3dx).yx( 233
=++

I-2005110
Solución:
Debido a que las potencias o las sumas de potencias de todos los componentes dan “3” (“x3
”,
“y3
”, “x.y2
”), la ecuación está conformada por funciones homogéneas de grado “3”, por lo
que puede ser resuelta mediante sustitución de variables.
dv.xdx.vdy +=
Reemplazando “y” y “dy” en la ecuación diferencial original se tiene:
( ) 0)dv.xdx.v.()x.v.(x3dx.)x.v(x 233
=+++
Resolviendo:
0)dv.xdx.v.(x.v3dx.x.vdx.x 32333
=+++
0dv.x.v3dx.x.v3dx.x.vdx.x 4233333
=+++
Factorando “x3
”:
0)dv.x.v3dx.v3dx.vdx(x 2333
=+++
Simplificando:
0dv.x.v3dx.v3dx.vdx 233
=+++
0dv.x.v3dx.v4dx 23
=++
Agrupando de acuerdo a las diferenciales:
0dv.x.v3)dx.v4dx( 23
=++
0dv.x.v3dx).v41( 23
=++
0
x).v41(
dv.x.v3dx).v41(
3
23
=
+
++
Simplificando:
0
x).v41(
dv.x.v3
x).v41(
dx).v41(
3
2
3
3
=
+
+
+
+
0
)v41(
dv.v3
x
dx
3
2
=
+
+

I-2005111
C
)v41(
dv.v3
x
dx
3
2
=
+
+ ∫∫
C)v41ln(
4
1
)xln( 3
=++
C4)v41ln()xln(4 3
=++
Introduciendo el número “4” en la expresión logarítmica:
C4)v41ln()xln( 34
=++
Reemplazando la constante “4C” por “ln(k)”:
)kln()v41ln()xln( 34
=++
Agrupando logaritmos:
( ) )kln()v41.(xln 34
=+
k)v41.(x 34
=+ Solución intermedia
x
y
v =
k
x
y
41.x
3
4
=














+
Destruyendo los signos de agrupación:
k
x
y
.x4x
3
44
=





+
k
x
y.x4
x
3
34
4
=+
Simplificando:
ky.x4x 34
=+ Solución
Donde:

I-2005112
0dx.yxdx.ydy.x 22
=−−−
Solución:
Debido a que las potencias simplificadas de todos los componentes dan “1” (“x”, “y”,
“ 22
yx + ”), la ecuación está conformada por funciones homogéneas de grado “1”, por lo
que puede ser resuelta mediante sustitución de variables.
dv.xdx.vdy +=
0dx.)x.v(xdx).x.v()dv.xdx.v.(x 22
=−−−+
Resolviendo:
0dx.)v1(xdx.x.vdv.xdx.v.x 222
=−−−+
0dx.v1.xdv.x 22
=−−
Factorando “x”:
0dx.v1dv.x.x 2
=




 −−
Simplificando:

I-2005113
0dx.v1dv.x 2
=−−
0
v1.x
dx.v1dv.x
2
2
=
−
−−
Simplificando:
0
v1.x
dx.v1
v1.x
dv.x
2
2
2
=
−
−
−
−
0
x
dx
v1
dv
2
=−
−
0
x
dx
v1
dv
2
=−
−
∫∫
C)xln()v(Sen 1
=−−
Reemplazando la constante “C” por “ln(k)”:
)kln()xln()v(Sen 1
=−−
)kln()xln()v(Sen 1
+=−
)x.kln()v(Sen 1
=−
Solución intermedia
x
y
v =
)x.kln(
x
y
Sen
1
=




−
Solución
Donde:
NOTA: Para representar gráficamente a la función se necesita calcular el Seno de las 2
expresiones.
{ })x.kln(Sen
x
y
SenSen 1
=











−

I-2005114
Simplificando:
{ })x.kln(Sen
x
y
=
{ })x.kln(Sen.xy = Solución para graficación
0dy).xy(dx).y3x2( =−++
Solución:
Debido a que las potencias de todos los componentes dan “1” (“2x”, “3y”, “y”, “-x”), la
ecuación está conformada por funciones homogéneas de grado “1”, por lo que puede ser
resuelta mediante sustitución de variables.
dv.xdx.vdy +=
0)dv.xdx.v).(xx.v(dx).x.v3x2( =+−++
Agrupando las expresiones con el mismo diferencial:
0dv.x).xx.v(dx.v).xx.v(dx).x.v3x2( =−+−++
0dv).1v(xdx).x.vx.v(dx).x.v3x2( 22
=−+−++
0dv).1v(xdx).x.vx.vx.v3x2( 22
=−+−++
Simplificando:

I-2005115
0dv).1v(xdx).x.vx.v2x2( 22
=−+++
0dv).1v(xdx).vv22.(x 22
=−+++
Dividiendo para el divisor de integración:
0
x).vv22(
dv).1v(xdx).vv22.(x
22
22
=
++
−+++
0
x).vv22(
dv).1v(x
x).vv22(
dx).vv22.(x
22
2
22
2
=
++
−
+
++
++
Simplificando:
0
vv22
dv).1v(
x
dx
2
=
++
−
+
Completando en el numerador de la segunda fracción la mitad de la derivada del
denominador:
0
vv22
dv).21v(
x
dx
2
=
++
−+
+
Separando la segunda fracción en 2:
0
vv22
dv2
vv22
dv).1v(
x
dx
22
=
++
−
++
+
+
0
vv22
dv2
vv22
dv).2v2(
.
2
1
x
dx
22
=
++
−
++
+
+
Integrando:
C
vv22
dv2
vv22
dv).2v2(
.
2
1
x
dx
22
=
++
−
++
+
+ ∫∫∫
C
vv22
dv2
)vv22ln(.
2
1
)xln(
2
2
=
++
−+++ ∫
Agrupando el denominador en un trinomio cuadrado perfecto:
C
1)1v2v(
dv
2)vv22ln(.
2
1
)xln(
2
2
=
+++
−+++ ∫
C
1)1v(
dv
2)vv22ln(.
2
1
)xln(
2
2
=
++
−+++ ∫
C)1v(Tan2)vv22ln(.
2
1
)xln( 12
=+−+++ −
Multiplicando por 2:

I-2005116
C2)1v(Tan4)vv22ln()xln(.2 12
=+−+++ −
Reemplazando “2C” por “k”:
k)1v(Tan4)vv22ln()xln( 122
=+−+++ −
La suma de logaritmos es el logaritmo del producto:
{ } k)1v(Tan4)vv22.(xln 122
=+−++ −
Solución intermedia
x
y
v =
k1
x
y
Tan4
x
y
x
y
22.xln
1
2
2
=





+−






















+





+
−
Simplificando:
k1
x
y
Tan4
x
y
x
x
y
x2x2ln 1
2
2
222
=






+−








⋅+⋅+ −
{ } k1
x
y
Tan4yy.x2x2ln
122
=






+−++
−
Solución
3.4.2 Ecuaciones Diferenciales con Relaciones Expresas entre las Variables:
Cuando se dispone de ecuaciones diferenciales con relaciones expresas entre las variables
puede ser conveniente introducir una nueva variable tal que refleje esas relaciones expresas.
[ ] 0dy.
y
x
1.e2dx.e21 )y/x()y/x(
=





−++
Solución:
Debido a la presencia de expresiones de la forma “x/y”, la relación para la sustitución de
variables es directamente identificable:
y
x
v = o y.vx = Ecuación de cambio de variable
dv.ydy.vdx +=
Reemplazando “x” y “dx”en la ecuación diferencial original se tiene:

I-2005117
0dy).
y
y.v
1(e2)dv.ydy.v).(e21(
y
y.v
y
y.v
=−+++












Simplificando:
0dy).v1(e2)dv.ydy.v).(e21( vv
=−+++
0dy.v.e2dy.e2dv.y.e2dy.v.e2dv.ydy.v vvvv
=−++++
0dy.e2dv.y.e2dv.ydy.v vv
=+++
Agrupando diferenciales:
0)dv.y.e2dv.y()dy.e2dy.v( vv
=+++
Factorando:
0dv).y.e2y(dy).e2v( vv
=+++
0dv).e21.(ydy).e2v( vv
=+++
Simplificando mediante el divisor de integración:
0
y).e2v(
dv).e21.(ydy).e2v(
v
vv
=
+
+++
0
y).e2v(
dv).e21.(y
y).e2v(
dy).e2v(
v
v
v
v
=
+
+
+
+
+
Simplificando:
0
e2v
dv).e21(
y
dy
v
v
=
+
+
+
Integrando:
0
e2v
dv).e21(
y
dy
v
v
=
+
+
+ ∫∫
C)e2vln()yln( v
=++
Reemplazando “C” por el logaritmo natural de “k”:
)kln()e2vln()yln( v
=++
la suma de logaritmos es el logaritmo del producto:
( ) )kln()e2v.(yln v
=+

I-2005118
k)e2v.(y v
=+
Destruyendo el paréntesis:
ke.y2v.y v
=+ Solución intermedia
y
x
v =
ke.y2
y
x
.y )y/x(
=+
Simplificando:
ke.y2x )y/x(
=+ Solución
La información en la hoja electrónica que permite generar la familia de curvas se obtiene
asignando valores a “x” y buscando mediante “prueba y error” los valores de “y” que
permiten cumplir con la “función primitiva”.

I-2005119
0dy)xyx(dx)yxxy1( 2322
=⋅−+⋅+−
Solución:
La ecuación de cambio de variable es:
y.xv = Ecuación de cambio de variable
Equivalente a:
x
v
y =
2
x
dx.vdv.x
dy
−
=
Reemplazando “y” y “dy”:
0
x
dx.vdv.x
x
x
v
xdx
x
v
x
x
v
x1 2
23
2
2
=




 −
⋅






−





+⋅














+





−
Simplificando:
0
x
dx.vdv.x
)xv.x(dx)vv1(
2
222
=




 −
⋅−+⋅+−
0
x
dx.vdv.x
)1v(xdx)vv1(
2
22
=




 −
⋅−+⋅+−
0)dx.vdv.x()1v(dx)vv1( 2
=−⋅−+⋅+−
Destruyendo paréntesis:
0)dx.vdv.xdx.vdv.v.x()dx.vdx.vdx( 22
=+−−++−
0)dv.xdv.v.x()dx.vdx.vdx.vdx.vdx( 22
=−++−+−
Simplificando:
0dv.x).1v()dx( =−+
Dividiendo para “x” que es el divisor de integración:
0
x
dv.x).1v(dx
=
−+
Separando en 2 fracciones y simplificando:

I-2005120
0
x
dv.x).1v(
x
dx
=
−
+
0dv).1v(
x
dx
=−+
Integrando:
Cdv).1v(
x
dx
=−+ ∫∫
Cv
2
v
)xln(
2
=−+ Solución intermedia
y.xv =
C)y.x(
2
y.x
)xln(
22
=−+ Solución
2
)yx(
dx
dy
−=
Solución:
Separando las diferenciales de la ecuación se tiene:
dx.)yx(dy 2
−=
Las expresiones que aparecen en la ecuación diferencial sugieren la siguiente transformación:

I-2005121
yxv −= Ecuación de cambio de variable
Equivalente a:
vyx +=
dvdydx +=
Reemplazando “x” y “dx” y simplificando:
[ ] )dvdy.(y)vy(dy 2
+−+=
( ) )dvdy.(yvydy 2
+−+=
)dvdy.(vdy 2
+=
Destruyendo el paréntesis:
dv.vdy.vdy 22
+=
dv.vdy.vdy 22
=−
dv.vdy).v1( 22
=−
Separando variables:
dv.
v1
v
dy
2
2
−
=
Separando la parte entera de la parte no divisible de la fracción:
1v
v
v1
v
2
2
2
2
−
−=
−
1v
1)1v(
v1
v
2
2
2
2
−
+−
−=
−
1v
1
1v
)1v(
v1
v
22
2
2
2
−
−
−
−
−=
−
1v
1
1
v1
v
22
2
−
−−=
−
Reemplazando en la expresión diferencial anterior:
dv.
v1
v
dy
2
2
−
=
dv.
1v
1
1dy 2 





−
−−=

I-2005122
Factorando el denominador de la fracción:
dv.
)1v).(1v(
1
1dy 





−+
−−=
Descomponiendo en Fracciones Parciales la expresión fraccionaria:
1v
B
1v
A
)1v).(1v(
1
−
+
+
=
−+
−
)1v).(1v(
)1v.(B)1v.(A
)1v).(1v(
1
−+
++−
=
−+
−
Destruyendo paréntesis en el numerador derecho:
)1v).(1v(
Bv.BAv.A
)1v).(1v(
1
−+
++−
=
−+
−
Agrupando:
)1v).(1v(
)AB(v).BA(
)1v).(1v(
1
−+
−++
=
−+
−
Al igualar los polinomios de las 2 fracciones se tiene el siguiente par de ecuaciones:
1AB
0BA
−=−
=+
2/1A =
2/1B −=
1v
2/1
1v
2/1
)1v).(1v(
1
−
−
+
+
=
−+
−
Reemplazando en la expresión diferencial:
dv.
1v
2/1
1v
2/1
1dy 





−
−
+
+−=
Separando componentes:
dv.
1v
2/1
dv.
1v
2/1
dvdy
−
−
+
+−=
1v
dv
2
1
1v
dv
2
1
dvdy
−
⋅−
+
⋅+−=
Integrando:
∫∫∫∫ −
−
+
+−=
1v
dv
2
1
1v
dv
2
1
dvdy

I-2005123
C)1vln(
2
1
)1vln(
2
1
vy +−−++−= Solución intermedia
yxv −=
C)1yxln(
2
1
)1yxln(
2
1
)yx(y +−−−+−+−−= Solución
3.4.3 Ecuaciones Diferenciales con Funciones Linealmente Dependientes:
Cuando se dispone de ecuaciones diferenciales con dependencia lineal entre las expresiones
que involucran a las variables que afectan a las diferenciales, es apropiado reemplazar una de
esas relaciones lineales por una nueva variable.
0dy).4y3x3(dx).yx( =−+++
Solución:
Las expresiones “x+y” y “3x+3y” (el segundo polinomio en función de las variables es un
múltiplo del primero por lo que son linealmente dependientes) dejan traslucir la conveniencia
de un cambio de variable del tipo:
yxv += o xvy −= Ecuación de cambio de variable
dxdvdy −=
[ ] 0)dxdv.(4)xv(3x3dx).xvx( =−−−++−+
Simplificando:
( ) 0)dxdv.(4x3v3x3dx.v =−−−++
( ) 0)dxdv.(4v3dx.v =−−+
Reagrupando:
( ) 0dv.4v3dx).4v3v( =−++−
( ) 0dv.4v3dx).v24( =−+−
Separando variables y diferenciales de esas variables:
( )dv.v34dx).v24( −=−
Factorando el miembro izquierdo:
( )dv.v34dx).v2(2 −=−
Trasladando las expresiones en “v” al miembro derecho:

I-2005124
dv.
v2
v34
dx.2 





−
−
=
Separando la parte entera de la parte fraccionaria:
dv.
v2
2)v36(
dx.2 





−
−−
=
dv.
v2
2
dv.
v2
v36
dx.2
−
−
−
−
=
dv.
v2
2
dv.3dx.2
−
−=
Integrando:
∫∫∫ −
−= dv.
v2
2
dv.3dx.2
C)v2ln(2v3x2 +−+=
Reemplazando “C” por el logaritmo natural de “k”:
)kln()v2ln(v3x2 2
+−+=
{ }2
)v2.(klnv3x2 −+= Solución intermedia
yxv +=
{ }2
)yx2.(kln)yx(3x2 −−++=
{ }2
)yx2.(klny3x3x2 −−++=
Pasando todas las expresiones al miembro izquierdo y cambiando de signo:
{ } 0x2)yx2.(klny3x3 2
=−−−++
{ } 0)yx2.(klny3x 2
=−−++ Solución
NOTA: Para la utilización del artificio propuesto se han comparado exclusivamente las partes
que contienen las variables, dentro de los polinomios que multiplican a las diferenciales; se
han ignorado los términos independientes.

I-2005125
NOTA: La representación gráfica de la solución no es directa sino que requiere la evaluación
de la función para algunos valores de la variable independiente “x”, a partir de lo cual se
estima el valor aproximado de la variable dependiente “y” que le corresponda.
0dy).y2x2(dx).1yx( =++−+
Solución:
Las expresiones “x+y” y “2x+2y”, donde la segunda expresión es múltiplo de la primera,
determinan la siguiente transformación:
yxv += o xvy −= Ecuación de cambio de variable
Las diferenciales correspondientes son:
dxdvdy −=
Reemplazando en la ecuación diferencial las equivalencias de “y” y “dy”, en función de la
nueva variable “v”, se tiene:
{ } { } 0)dxdv.()xv(2x2dx.1)xv(x =−−++−−+
Simplificando y agrupando las diferenciales:
{ } { } 0)dxdv.(x2v2x2dx.1xvx =−−++−−+
Simplificando:
0)dxdv.(v2dx).1v( =−+−
0dx.v2dv.v2dxdx.v =−+−
0dv.v2dxdx.v =+−−
Agrupando:
0dv.v2dx).1v( =++−

I-2005126
dx).1v(dv.v2 +=
dxdv.
1v
v2
=
+
∫∫ =
+
dxdv.
1v
v2
Reemplazando la fracción de la integral izquierda por su equivalente:
∫∫ =





+
− dxdv.
1v
2
2
Cx)1vln(.2v2 +=+−
Trasladando “x” al miembro izquierdo:
Cx)1vln(.2v2 =−+−
Cx)1vln(.2v2 =−+− Solución intermedia
yxv +=
Cx)1yxln(.2)yx(2 =−++−+
Simplificando:
Cx)1yxln(.2y2x2 =−++−+
C)1yxln(.2y2x =++−+ Solución

I-2005127
3.4.4 Ecuaciones Diferenciales con Funciones Lineales Independientes no Homogéneas:
Cuando se dispone de ecuaciones diferenciales con funciones lineales independientes no
homogéneas es conveniente encontrar transformaciones lineales de las variables de modo que
se pueda obtener una Ecuación Diferencial Equivalente con Funciones Homogéneas.
Posteriormente se resuelve la ecuación como se describió en el numeral anterior.
Es importante asegurarse que las expresiones de las variables (no se toman en consideración
los términos independientes) que acompañan a las 2 diferenciales no sean linealmente
dependientes como en los problemas inmediatamente anteriores.
0dy).2y4x2(dx).5yx( =+−+−+
Solución:
Debido a que los factores que multiplican a las diferenciales no son proporcionales en la parte
que corresponde a las variables, no es posible aplicar el artificio anterior.
Por tener una ecuación lineal no homogénea es necesario transformarla en una ecuación lineal
homogénea. Para encontrar las expresiones que permitan la simplificación de la ecuación
diferencial se deben resolver como simultáneas las expresiones que multiplican a las
diferenciales, igualadas a cero:
02y4x2
05yx
=+−
=−+
La solución al sistema de ecuaciones es:
3x =
2y =
Las variables “x” y “y” deben ser reemplazadas por nuevas variables “s” y “t”, mediante las
siguientes ecuaciones paramétricas que toman en consideración los valores solución del
sistema de ecuaciones:
3xs −= o 3sx += Ecuación 1 de cambio de variable
2yt −= o 2ty += Ecuación 2 de cambio de variable
dsdx =
dtdy =
Reemplazando las expresiones anteriores en la ecuación diferencial se tiene:
{ } { } 0dt.2)2t(4)3s(2ds.5)2t()3s( =++−++−+++
Simplificando:
{ } { } 0dt.28t46s2ds.52t3s =+−−++−+++
{ } { } 0dt.t4s2ds.ts =−++ Ecuación diferencial intermedia 1

I-2005128
La nueva ecuación es lineal homogénea.
La resolución del sistema de ecuaciones simultáneas, basada en los factores que
afectan a las diferenciales “dx” y “dy”, es equivalente a la búsqueda de un nuevo
centro de coordenadas que coincide con la intersección de las 2 rectas, por lo que
luego de realizar la traslación de ejes al utilizar las nuevas variables, definidas
por esa coordenada de intersección, los factores que afectan a las diferenciales
carecen de términos independientes, pues las rectas que representan esos factores
pasan por el nuevo eje de coordenadas.
Se requiere de un segundo cambio de variable del siguiente tipo:
s.vt = o
s
t
v = Ecuación 3 de cambio de variable
dv.sds.vdt +=
Reemplazando “t” y “dt”:
{ } { } 0)dv.sds.v.(s.v4s2ds.s.vs =+−++
Dividiendo para “s”:
0)dv.sds.v).(v42(ds).v1( =+−++
Simplificando:
0)dv.s.v4ds.v4dv.s2ds.v2()ds.vds( 2
=−−+++
Destruyendo signos de agrupación:
0dv.s.v4ds.v4dv.s2ds.v2ds.vds 2
=−−+++

I-2005129
0)dv.s.v4dv.s2()ds.v4ds.v2ds.vds( 2
=−+−++
0dv).s.v4s2(ds).v4v2v1( 2
=−+−++
Simplificando:
0dv).v42(sds).v4v31( 2
=−+−+
Factorando:
0dv).v42(sds).v1)(v41( =−+−+
Dividiendo para “s.(1+4v).(1-v)” que es el divisor de integración:
0
)v1).(v41.(s
dv).v42(sds).v1)(v41(
=
−+
−+−+
0
)v1).(v41.(s
dv).v42(s
)v1).(v41.(s
ds).v1)(v41(
=
−+
−
+
−+
−+
0
)v1).(v41(
dv).v42(
s
ds
=
−+
−
+ Ecuación diferencial intermedia 2
Descomponiendo la segunda fracción en fracciones parciales y reemplazando:
v1
B
v41
A
)v1).(v41(
v42
−
+
+
=
−+
−
)v1).(v41(
)v41.(B)v1.(A
)v1).(v41(
v42
−+
++−
=
−+
−
Destruyendo paréntesis en el numerador:
)v1).(v41(
v.B4Bv.AA
)v1).(v41(
v42
−+
++−
=
−+
−
Agrupando:
)v1).(v41(
v).AB4()BA(
)v1).(v41(
v42
−+
−++
=
−+
−
De donde, al igualar los polinomios de las 2 fracciones se tiene:
4AB4
2BA
−=−
=+
5/2A −=
5/12B =
v1
5/12
v41
5/2
)v1).(v41(
v42
−
+
+
−
=
−+
−
Reemplazando en la Ecuación Diferencial Intermedia 2 se tiene:

I-2005130
0
v1
dv).5/12(
v41
dv).5/2(
s
ds
=
−
+
+
−
+
0
v1
dv
5
12
v41
dv
5
2
s
ds
=
−
⋅+
+
⋅−
Integrando:
0
v1
dv
5
12
v41
dv
5
2
s
ds
=
−
⋅+
+
⋅− ∫∫∫
0C)v1ln(
5
12
)v41ln(
10
1
)sln( =+−−+− Solución intermedia 1
Reemplazando la tercera ecuación de cambio de variable:
s
t
v =
0C
s
t
1ln
5
12
s
t4
1ln
10
1
)sln( =+





−−





+− Solución intermedia 2
Reemplazando las 2 primeras ecuaciones de cambio de variable:
3xs −=
2yt −=
0C
3x
2y
1ln
5
12
3x
)2y(4
1ln
10
1
)3xln( =+





−
−
−−





−
−
+−− Solución
0dy).1xy4(dx).1yx( =−++−−
Solución:
La ecuación es lineal no homogénea y requiere ser transformada en una ecuación lineal
homogénea. El sistema de ecuaciones simultáneas que permite esa simplificación es:
01xy4
01yx
=−+
=−−
1x =
0y =
Las variables “x” y “y” deben ser reemplazadas por nuevas variables “s” y “t”, mediante las
siguientes ecuaciones paramétricas:
1xs −= o 1sx += Ecuación 1 de cambio de variable

I-2005131
yt = o ty = Ecuación 2 de cambio de variable
dsdx =
dtdy =
Reemplazando las expresiones anteriores en la ecuación diferencial se tiene:
{ } { } 0dt.1)1s()t(4ds.1)t()1s( =−+++−−+
Simplificando:
{ } { } 0dt.11st4ds.1t1s =−+++−−+
0dt)st4(ds)ts( =⋅++⋅− Ecuación diferencial intermedia 1
Se requiere de un segundo cambio de variable del siguiente tipo:
s.vt = o
s
t
v = Ecuación 3 de cambio de variable
dv.sds.vdt +=
{ } { } 0)dvsdsv(s)sv(4ds)sv(s =⋅+⋅⋅+⋅+⋅⋅−
0)dvsdsv()1v4(ds)v1( =⋅+⋅⋅++⋅−
Simplificando y destruyendo signos de agrupación:
0)dv.sds.vdv.s.v4ds.v4()ds.vds( 2
=++++−
0dv.sds.vdv.s.v4ds.v4ds.vds 2
=++++−
0)dv.sdv.s.v4()ds.vds.v4ds.vds( 2
=++++−
0dv).ss.v4(ds).vv4v1( 2
=++++−
0dv).ss.v4(ds).v41( 2
=+++
Factorando:
0dv).1v4.(sds).v41( 2
=+++
Dividiendo para “s.(1+4v2
)” que es el divisor de integración:
0
)v41.(s
dv).1v4.(sds).v41(
2
2
=
+
+++

I-2005132
0
)v41.(s
dv).1v4.(s
)v41.(s
ds).v41(
22
2
=
+
+
+
+
+
0
v41
dv).1v4(
s
ds
2
=
+
+
+
0
v41
dv
v41
dv.v4
s
ds
22
=
+
+
+
+ Ecuación diferencial intermedia 2
Integrando:
0
v41
dv
v41
dv.v4
s
ds
22
=
+
+
+
+ ∫∫∫
0C)v.2(Tan)v41ln(
2
1
)sln( 12
=++++ −
Solución intermedia 1
Reemplazando la tercera ecuación de cambio de variable:
s
t
v =
0C
s
t2
Tan
s
t4
1ln
2
1
)sln( 1
2
2
=+





+








++ −
Reemplazando las 2 primeras ecuaciones de cambio de variable:
1xs −=
yt =
0C
1x
y2
Tan
)1x(
y4
1ln
2
1
)1xln( 1
2
2
=+





−
+








−
++− −
Solución
NOTA: Para enfrentar la resolución de nuevas formas de ecuaciones diferenciales se busca
una aproximación a esquemas cuya solución ya se conoce, a través de manejos algébricos. El
cambio de variables es uno de los mecanismos más apropiados para lograr esa aproximación.
3.4.5 Ecuaciones Diferenciales No Convencionales:
Cuando se dispone de ecuaciones diferenciales no convencionales es apropiado realizar
reemplazos por nuevas variables que conduzcan a la simplificación de la ecuación diferencial,
y permitan su aproximación hacia las formas convencionales.
0dy.y).8y2x3(dx.x).7y3x2( 2222
=−+−−+

I-2005133
Solución:
Por la forma de las expresiones y de sus diferenciales es conveniente realizar los siguientes
reemplazos de variables:
2
xu = Ecuación 1 de cambio de variable
2
yv = Ecuación 2 de cambio de variable
dx.x2du =
dy.y2dv =
Reemplazando “x” y “y”, “dx” y “dy” en la ecuación diferencial:
0
2
dv
).8v2u3(
2
du
).7v3u2( =−+−−+
0dv).8v2u3(du).7v3u2( =−+−−+ Ecuación diferencial intermedia 1
La ecuación es lineal no homogénea y requiere ser transformada en una ecuación lineal
homogénea mediante otro cambio de variables. El sistema de ecuaciones simultáneas que
permite esa simplificación es:
08v2u3
07v3u2
=−+
=−+
2u =
1v =
Las variables “u” y “v” deben ser reemplazadas por nuevas variables “s” y “t”, mediante las
siguientes ecuaciones paramétricas:
2us −= o 2su += Ecuación 3 de cambio de variable
1vt −= o 1tv += Ecuación 4 de cambio de variable
dsdu =
dtdv =
Reemplazando las expresiones anteriores en la ecuación diferencial intermedia 1 se tiene:
{ } { } 0dt.8)1t(2)2s(3ds.7)1t(3)2s(2 =−+++−−+++
Simplificando:
{ } { } 0dt.82t26s3ds.73t34s2 =−+++−−+++
{ } { } 0dt.t2s3ds.t3s2 =+−+ Ecuación diferencial intermedia 2
Se requiere de un nuevo cambio de variables del siguiente tipo:

I-2005134
s.wt = o
s
t
w = Ecuación 5 de cambio de variable
dw.sds.wdt +=
{ } { } 0)dw.sds.w.()s.w(2s3ds.)s.w(3s2 =++−+
0)dw.sds.w).(s.w2s3(ds).s.w3s2( =++−+
0)dw.sds.w).(w23(sds).w32(s =++−+
0)dw.sds.w).(w23(ds).w32( =++−+
Simplificando y destruyendo signos de agrupación:
0)dw.w.s2ds.w2dw.s3ds.w3()ds.w3ds2( 2
=+++−+
0dw.w.s2ds.w2dw.s3ds.w3ds.w3ds2 2
=−−−−+
0)dw.w.s2dw.s3()ds.w2ds.w3ds.w3ds2( 2
=+−−−+
0dw).w.s2s3(ds).w2w3w32( 2
=+−−−+
0dw).w23(sds).w22( 2
=+−−
Factorando:
0dw).w23(sds).w1)(w1(2 =+−+−
Dividiendo para “s.(1-w).(1+w)” que es el divisor de integración:
0
)w1).(w1.(s
dw).w23.(sds).w1).(w1(2
=
+−
+−+−
0
)w1).(w1.(s
dw).w23.(s
)w1).(w1.(s
ds).w1).(w1(2
=
+−
+
−
+−
+−
0
)w1).(w1(
dw).w23(
s
ds2
=
+−
+
−
Descomponiendo en fracciones parciales la segunda expresión:
w1
B
w1
A
)w1).(w1(
w23
+
+
−
=
+−
−−
Obteniendo denominador común:
)w1).(w1(
)w1(B)w1(A
)w1).(w1(
w23
+−
−++
=
+−
−−

I-2005135
)w1).(w1(
w.BBw.AA
)w1).(w1(
w23
+−
−++
=
+−
−−
Agrupando en un polinomio al numerador derecho:
)w1).(w1(
w).BA()BA(
)w1).(w1(
w23
+−
−++
=
+−
−−
Igualando los polinomios de los numeradores se tiene el siguiente sistema de
ecuaciones:
2BA
3BA
−=−
−=+
2
5
A −=
2
1
B −=
Reemplazando en la expresión general de las fracciones parciales se tiene:
w1
B
w1
A
)w1).(w1(
w23
+
+
−
=
+−
−−
w1
2
1
w1
2
5
)w1).(w1(
w23
+
−
+
−
−
=
+−
−−
Reemplazando las fracciones parciales en la ecuación diferencial:
0
)w1).(w1(
dw).w23(
s
ds2
=
+−
+
−
0dw
w1
2
1
dw
w1
2
5
s
ds2
=⋅
+
−⋅
−
−
0
w1
dw
2
1
w1
dw
2
5
s
ds2
=
+
⋅−
−
⋅− Ecuación diferencial intermedia 2
Integrando:
C
w1
dw
2
1
w1
dw
2
5
s
ds2
=
+
−
−
− ∫∫∫
C)w1ln(
2
1
)w1ln(
2
5
)sln(2 =+−−−
Pasando los logaritmos negativos al miembro derecho:
C)w1ln(
2
1
)w1ln(
2
5
)sln(2 +++−=
C2)w1ln()w1ln(5)sln(4 +++−=

I-2005136
Reemplazando “2C” por el “ln(k)”:
)kln()w1ln()w1ln(5)sln(4 +++−=
Introduciendo los coeficientes en los logaritmos:
( ) ( ) )kln(w1lnw1ln)sln( 54
+++−=
Agrupando los logaritmos:
( ) ( ){ }w1.w1.kln)sln( 54
+−=
Calculando antilogaritmos:
( ) ( )w1.w1.ks 54
+−= Solución intermedia 1
Reemplazando la quinta ecuación de cambio de variable:
s
t
w =






+





−=
s
t
1.
s
t
1.ks
5
4
Reemplazando la tercera y la cuarta ecuaciones de cambio de variable:
2us −=
1vt −=






−
−
+





−
−
−=−
2u
1v
1.
2u
1v
1.k)2u(
5
4
Reemplazando la primera y segunda ecuaciones de cambio de variable:
2
xu =
2
yv =








−
−
+








−
−
−=−
2x
1y
1.
2x
1y
1.k)2x(
2
2
5
2
2
42
Solución

I-2005137
3.5 RESOLUCIÓN BASADA EN PROPIEDADES DE LAS ECUACIONES
DIFERENCIALES:
3.5.1 Ecuaciones Diferenciales Lineales Exactas:
Dada la ecuación diferencial de la forma:
0dy).y,x(Ndx).y,x(M =+
La ecuación es una diferencial exacta de una función primitiva “F(x, y)” si se cumple que:
x
N
y
M
∂
∂
=
∂
∂
Cuando se menciona que la ecuación “M(x,y).dx+N(x,y).dy=0” es una diferencial exacta de
una función primitiva se hace referencia al hecho de que al diferenciar la función “F(x,y)”,
antes de eliminar cualquier expresión factorada, se obtiene exactamente la ecuación
diferencial propuesta.
La ecuación diferencial, en función de la expresión primitiva, se puede escribir como:
0)y,x(dFdy.Ndx.M ==+
Donde “dF” es una diferencial exacta cuya solución es:
C)y,x(dF =∫
C)y,x(F =
El diferencial de la función primitiva “F” se puede calcular como:
dy.
y
F
dx.
x
F
)y,x(dF
∂
∂
+
∂
∂
=
Donde:

I-2005138
dy).y,x(Ndx).y,x(Mdy.
y
F
dx.
x
F
)y,x(dF +=
∂
∂
+
∂
∂
=
Claramente se puede determinar que:
dx).y,x(Mdx.
x
F
=
∂
∂
De donde:
)y(dx).y,x(M)y,x(F
x
φ+= ∫
Donde:
∫
x
: Integración respecto a “x” tratando a “y” como constante
φ(y): Constante de integración respecto a “x”.
Obteniendo la derivada parcial de la expresión anterior, respecto a “y”:
)y,x(N
dy
d
dx).y,x(M
yy
F x
=
φ
+






∂
∂
=
∂
∂
∫
)y,x(N)y(dx).y,x(M
yy
F x
=φ′+






∂
∂
=
∂
∂
∫
La expresión previa nos permite determinar la expresión de “φ′ ”:






∂
∂
−=φ′ ∫
x
dx).y,x(M
y
)y,x(N)y(
Lo que por integración nos permite calcular “φ(y)” y por consiguiente determinar “F(x, y)”.
Es importante notar que las derivadas parciales cruzadas también pueden ser representadas de
la siguiente manera:
x.y
F
x
F
yy
M 2
∂∂
∂
=





∂
∂
∂
∂
=
∂
∂
y.x
F
y
F
xx
N 2
∂∂
∂
=





∂
∂
∂
∂
=
∂
∂
Con las 2 expresiones anteriores se evidencia la razón por la que las derivadas parciales
cruzadas deben ser iguales.
y.x
F
x.y
F 22
∂∂
∂
=
∂∂
∂
→
x
N
y
M
∂
∂
=
∂
∂
Ejemplo 2:
0dy).1yx3(dx).y3x2( 3
=−+++
Las funciones definidas en la propiedad de originarse en una diferencial exacta son:

I-2005139
y3x2M 3
+=
1yx3N −+=
Se pueden obtener las derivadas parciales cruzadas:
3
y
)y3x2(
y
M 3
=
∂
+∂
=
∂
∂
3
x
)1yx3(
x
N
=
∂
−+∂
=
∂
∂
Debido a que las 2 derivadas parciales son iguales, la ecuación diferencial es exacta, y su
solución podría obtenerse mediante separación de variables o utilizando las ecuaciones
descritas anteriormente (las metodologías básicas se presentan en los siguientes problemas
resueltos).
Ejemplo 3:
0dy).1yx2(dx).7y4x( 32
=+−+++
Las funciones definidas en la propiedad anterior son:
7y4xM 2
++=
1yx2N 3
+−=
4
y
)7y4x(
y
M 2
=
∂
++∂
=
∂
∂
2
x
)1yx2(
x
N 3
=
∂
+−∂
=
∂
∂
Debido a que las 2 derivadas parciales son diferentes, la ecuación diferencial, tal como está
planteada, no proviene de una diferencial exacta de una función primitiva.
Resolver la ecuación diferencial del Ejemplo 2:
0dy).1yx3(dx).y3x2( 3
=−+++
Solución 1:
En el Ejemplo 2 se demostró que la ecuación diferencial propuesta proviene de una
diferencial exacta pues las derivadas cruzadas son exactamente iguales.
Destruyendo los signos de agrupación en la ecuación diferencial se tiene:
0dydy.ydy.x3dx.y3dx.x2 3
=−+++

I-2005140
Reagrupando los términos de la ecuación diferencial en función de que sean integrables
directamente o no lo sean:
0)dy.x3dx.y3()dydy.ydx.x2( 3
=++−+
Integrando:
C)dy.x3dx.y3()dydy.ydx.x2( 3
=++−+ ∫∫
C)dy.x3dx.y3(dydy.ydx.x2 3
=++−+ ∫∫∫∫
C)dy.x3dx.y3(y
2
y
4
x2 24
=++−+ ∫
La integral que queda pendiente es la derivada de la expresión “3y.x”, por lo que:
Cx.y3y
2
y
2
x 24
=+−+ Solución 1
Solución 2:
Se van a aprovechar las propiedades obtenidas para las ecuaciones diferenciales exactas. La
ecuación básica es:
0dy).1yx3(dx).y3x2( 3
=−+++
Las funciones “M” y “N” son:
y3x2M 3
+=
1yx3N −+=
La expresión para el cálculo de la función primitiva es:
)y(dx).y,x(M)y,x(F
x
φ+= ∫
)y(dx).y3x2()y,x(F
x 3
φ++= ∫
Ejecutando la integral respecto a “x”:
)y(x.y3x
4
2
)y,x(F 4
φ++= Función primitiva
“φ(y) ” es una función exclusiva de “y” cuyo valor aún se desconoce.
Obteniendo la derivada parcial de “F” respecto a “y”:
)y(x3
y
F
φ′+=
∂
∂
Pero:
)y,x(N
y
F
=
∂
∂

I-2005141
De donde:
1yx3)y(x3 −+=φ′+
Simplificando:
1y)y( −=φ′
Integrando “φ′ ” se obtiene “φ”:
∫ −=φ dy).1y()y(
yy
2
1
)y( 2
−=φ
La función primitiva es:
)y(x.y3x
4
2
)y,x(F 4
φ++=
Reemplazando “φ(y)”:
yy
2
1
x.y3x
2
1
)y,x(F 24
−++= Función primitiva
La ecuación primitiva es:
C)y,x(F =
Cx.y3y
2
y
2
x 24
=+−+ Solución 2
NOTA 1: Los dos métodos de solución proporcionan respuestas idénticas.
NOTA 2: A pesar de existir varias etapas en que se realizan integraciones, en la segunda
alternativa la Constante Arbitraria de Integración solamente se la aplica en la última instancia.

I-2005142
NOTA 3: Los pasos requeridos en la metodología para utilizar las propiedades de las
ecuaciones diferenciales que son diferenciales exactas de una Función Primitiva son:
Ø Determinar las funciones “M(x,y)” y “N(x,y)” a partir de la ecuación diferencial
original
Ø Verificar que la ecuación diferencial propuesta provenga de una diferencial exacta de
una “Función Primitiva” mediante el cumplimiento de que:
x
N
y
M
∂
∂
=
∂
∂
Ø Obtener la función primitiva “F(x,y)” de la ecuación diferencial, mediante una
integración con respecto a “x”, incluyendo una función “φ(y)” aún desconocida.
)y(dx).y,x(M)y,x(F
x
φ+= ∫
Ø Calcular la derivada parcial de la función primitiva “F(x,y)”, con respecto a “y” e
igualar a la función “N(x,y)”.
)y,x(N
dy
d
dx).y,x(M
yy
F x
=
φ
+






∂
∂
=
∂
∂
∫
Ø Determinar el valor de la derivada de “φ” con respecto a “y”.






∂
∂
−=
φ
=φ′ ∫
x
dx).y,x(M
y
)y,x(N
dy
d
)y(
Ø Integrar la expresión obtenida para calcular “φ”.
∫φ′=φ dy.)y(
Ø Una vez conocido “φ(y)” determinar la función primitiva completa mediante la
expresión:
)y(dx).y,x(M)y,x(F
x
φ+= ∫
{ } 0dy.1)1y(Seny.x4dx).y.x4e6( 222x3
=−+++++
Solución 1:
En primer lugar se debe verificar si la ecuación diferencial planteada es exacta.
Las funciones definidas para las ecuaciones diferenciales exactas son:
22x3
y.x4e6M += +
1)1y(Seny.x4N 2
−++=

I-2005143
y.x8
y
)y.x4e6(
y
M 22x3
=
∂
+∂
=
∂
∂ +
( ) y.x8
x
1)1y(Seny.x4
x
N 2
=
∂
−++∂
=
∂
∂
Debido a que las 2 derivadas parciales son iguales, la ecuación diferencial tiene
solución exacta.
0dydy).1y(Sendy.y.x4dx.y.x4dx.e6 222x3
=−+++++
( ) ( ) 0dy.y.x4dx.y.x4dydy).1y(Sendx.e6 222x3
=++−+++
Integrando:
( ) ( ) Cdy.y.x4dx.y.x4dydy).1y(Sendx.e6 222x3
=++−++ ∫∫
+
( ) Cdy.y.x4dx.y.x4dydy).1y(Sendx.e6 222x3
=++−++ ∫∫∫∫
+
( ) Cdy.y.x4dx.y.x4y)1y(Cose
3
6 222x3
=++−+− ∫
+
Simplificando:
( ) Cdy.y.x4dx.y.x4y)1y(Cose2 222x3
=++−+− ∫
+
La integral que queda pendiente es la derivada de la expresión “2x2
.y2
”, por lo que:
Cy.x2y)1y(Cose2 222x3
=+−+−+
Solución 1
Solución 2:
La ecuación diferencial básica es:
{ } 0dy.1)1y(Seny.x4dx).y.x4e6( 222x3
=−+++++
22x3
y.x4e6M += +
1)1y(Seny.x4N 2
−++=
)y(dx).y,x(M)y,x(F
x
φ+= ∫
)y(dx).y.x4e6()y,x(F
x 22x3
φ++= ∫
+

I-2005144
)y(y.x
2
4
e
3
6
)y,x(F 222x3
φ++= +
Simplificando:
)y(y.x2e2)y,x(F 222x3
φ++= +
Función primitiva
)y(y.x4
y
F 2
φ′+=
∂
∂
Pero:
)y,x(N
y
F
=
∂
∂
De donde:
1)1y(Seny.x4)y(y.x4 22
−++=φ′+
Simplificando:
1)1y(Sen)y( −+=φ′
{ }∫ −+=φ dy.1)1y(Sen)y(
y)1y(Cos)y( −+−=φ
)y(y.x2e2)y,x(F 222x3
φ++= +
y)1y(Cosy.x2e2)y,x(F 222x3
−+−+= +
C)y,x(F =
Cy.x2y)1y(Cose2 222x3
=+−+−+
Solución 2
NOTA: A pesar de la complejidad de la ecuación diferencial cuya solución se estaba
buscando, el procedimiento empleado en la Solución 2, que aprovecha las propiedades de las
ecuaciones diferenciales lineales exactas, es menos complicado.
0dy).y3e.y.x2(dx).x4e.y( 2y.x3y.x2 22
=−++
Solución 1:
Se debe verificar si la ecuación diferencial es exacta.

I-2005145
3y.x2
x4e.yM
2
+=
2y.x
y3e.y.x2N
2
−=
2222
2
y.xy.x3y.xy.x2
3y.x2
e.y2e.y.x2)y2(e)y.x2(e.y
y
)x4e.y(
y
M
+=+=
∂
+∂
=
∂
∂
2222
2
y.xy.x3y.x2y.x
2y.x
e.y2e.y.x2)1(e)y(e.xy2
x
)y3e.y.x2(
x
N
+=





+=
∂
−∂
=
∂
∂
Debido a que las 2 derivadas parciales son iguales, la ecuación diferencial es exacta.
0dy.y3dy.e.y.x2dx.x4dx.e.y 2y.x3y.x2 22
=−++
0)dy.e.y.x2dx.e.y()dy.y3dx.x4(
22
y.xy.x223
=++−
Integrando:
C)dy.e.y.x2dx.e.y()dy.y3dx.x4(
22
y.xy.x223
=++− ∫∫
C)dy.e.y.x2dx.e.y(dy.y3dx.x4
22
y.xy.x223
=++− ∫∫∫
C)dy.e.y.x2dx.e.y(
3
y3
4
x4 22
y.xy.x2
34
=++− ∫
C)dy.e.y.x2dx.e.y(yx
22
y.xy.x234
=++− ∫
Se debe resolver la integral que queda pendiente:
La integral es:
∫ + )dy.e.y.x2dx.e.y(
22
y.xy.x2
Es conveniente utilizar un cambio de variable:
2
y.xz = Ecuación de cambio de variable
Que es equivalente a:
2
y
z
x = o 2
y.zx −
=
La expresión diferencial equivalente es:
dz.ydy.y).2.(zdx 23 −−
+−=
dz.ydy.y.z2dx 23 −−
+−=
Reemplazando “x” y “dx” en la integral:

I-2005146
∫
∫
−−
−−−
++−
=+
)dy.e.y).y.z(2)dz.ydy.y.z2.(e.y(
)dy.e.y.x2dx.e.y(
2222
22
y).y.z(223y).y.z(2
y.xy.x2
Simplificando:
∫
∫
−−−
++−
=+
)dy.e.y).y.z(2)dz.ydy).y.z2.(e.y(
)dy.e.y.x2dx.e.y(
z223z2
y.xy.x2 22
∫ ∫∫∫
−−
++−=+ dy.e.y.z(2dz.edy.e.z.y2)dy.e.y.x2dx.e.y( z1zz1y.xy.x2 22
∫ ∫∫∫
−−
+−+=+ dy.e.y.z(2dy.e.z.y2dz.e)dy.e.y.x2dx.e.y( z1z1zy.xy.x2 22
zy.xy.x2
e)dy.e.y.x2dx.e.y(
22
=+∫
Reemplazando “z” en función de “x” y “y”:
222
y.xy.xy.x2
e)dy.e.y.x2dx.e.y( =+∫
Reemplazando la integral obtenida en la solución de la ecuación diferencial:
C)dy.e.y.x2dx.e.y(yx
22
y.xy.x234
=++− ∫
Ceyx
2
y.x34
=+− Solución1
Solución 2:
La ecuación diferencial básica es:
0dy).y3e.y.x2(dx).x4e.y( 2y.x3y.x2 22
=−++
3y.x2
x4e.yM
2
+=
2y.x
y3e.y.x2N
2
−=
)y(dx).y,x(M)y,x(F
x
φ+= ∫
)y(dx).x4e.y()y,x(F
x 3y.x2 2
φ++= ∫
)y(
4
x4
e.y.
y
1
)y,x(F
4
y.x2
2
2
φ++=
Simplificando:
)y(xe)y,x(F 4y.x 2
φ++= Función primitiva

I-2005147
)y(e.y.x2
y
F 2
y.x
φ′+=
∂
∂
Pero:
)y,x(N
y
F
=
∂
∂
De donde:
2y.xy.x
y3e.y.x2)y(e.y.x2
22
−=φ′+
Simplificando:
2
y3)y( −=φ′
∫−=φ dy.y3)y( 2
3
y)y( −=φ
)y(xe)y,x(F 4y.x 2
φ++=
34y.x
yxe)y,x(F
2
−+= Función primitiva
C)y,x(F =
Cyxe 34y.x 2
=−+ Solución 2

I-2005148
3.5.2 Ecuaciones Diferenciales Lineales No Exactas:
Dada la ecuación diferencial de la forma:
Si las derivadas parciales cruzadas de las funciones no son iguales, la ecuación se denomina
Lineal No Exacta.
x
N
y
M
∂
∂
≠
∂
∂
Para convertirla en Ecuación Diferencial Lineal Exacta, en algunos casos se puede obtener un
factor de integración “µ” tal que:
0dy).y,x(N.dx).y,x(M. =µ+µ
“Ecuación Diferencial Equivalente” en la que deberá cumplirse que:
x
)N.(
y
)M.(
∂
µ∂
=
∂
µ∂
Una vez obtenida la nueva expresión se puede resolver la ecuación mediante los
procedimientos para Ecuaciones Diferenciales Exactas.
Para obtener los factores de integración se pueden utilizar las siguientes reglas:
Condición Factor de Integración
)x(f
N
x
N
y
M
=
∂
∂
−
∂
∂ ∫=µ dx).x(f
e
* )y(g
M
x
N
y
M
−=
∂
∂
−
∂
∂ ∫=µ dy).y(g
e
* )y(g
M
y
M
x
N
=
∂
∂
−
∂
∂ ∫=µ dy).y(g
e
0dy).y,x(Ndx).y,x(M =+ es homogénea
y.Nx.M
1
+
=µ
Si la ecuación 0dy).y,x(Ndx).y,x(M =+ puede escribirse en la
forma 0dy).y.x(g.xdx).y.x(f.y =+ , y )y.x(g)y.x(f ≠ y.Nx.M
1
−
=µ
* Las 2 expresiones corresponden al mismo tipo de solución
0dy.y.xdx).xyx( 22
=+++
Solución:
En primer lugar se debe verificar si la ecuación diferencial planteada es exacta.

I-2005149
xyxM 22
++=
y.xN =
y2
y
)xyx(
y
M
22
=
∂
++∂
=
∂
∂
y
x
)y.x(
x
N
=
∂
∂
=
∂
∂
Debido a que las 2 derivadas parciales no son iguales, la ecuación diferencial no es exacta.
A pesar de que la ecuación diferencial no es exacta, una rápida inspección de las derivadas
parciales cruzadas revela que la diferencia entre las 2 derivadas, dividida para “N” es una
función de “x”.
y.x
yy2
N
x
N
y
M
−
=
∂
∂
−
∂
∂
Simplificando:
y.x
y
N
x
N
y
M
=
∂
∂
−
∂
∂
x
1
N
x
N
y
M
=
∂
∂
−
∂
∂
De donde:
x
1
)x(f =
El factor de integración “µ” es:
∫=µ dx).x(f
e
Reemplazando la función “f(x)”:
∫
=µ x
dx
e
Ejecutando la integral:
)xln(
e=µ
Por la relación entre el logaritmo natural y la función exponencial se tiene:
x=µ

I-2005150
Multiplicando la ecuación diferencial por el factor de integración “x” se tiene una “Ecuación
Diferencial Equivalente”:
{ } 0dy.y.xdx).xyx(.x 22
=+++
0dy.y.xdx).xy.xx( 2223
=+++ Ecuación diferencial equivalente
Para la nueva ecuación se deben redefinir las funciones “M” y “N”:
223
xy.xxM ++=
y.xN 2
=
Obteniendo las derivadas parciales cruzadas:
y.x2
y
M
=
∂
∂
y.x2
x
N
=
∂
∂
Debido a que las 2 expresiones son iguales, la nueva ecuación diferencial es exacta.
En este punto existen 2 caminos para resolver la ecuación diferencial: se pueden agrupar los
términos de modo que las funciones sean directamente integrables, o se pueden aprovechar las
propiedades matemáticas de las ecuaciones diferenciales exactas. En el presente caso
escogeremos la primera alternativa.
Destruyendo los signos de agrupación en la ecuación diferencial equivalente se tiene:
0dy.y.xdx.xdx.y.xdx.x 2223
=+++
0)dy.y.xdx.y.x()dx.xdx.x( 2223
=+++
Integrando:
C)dy.y.xdx.y.x(dx.xdx.x 2223
=+++ ∫∫∫
Ejecutando las 2 primeras integrales:
C)dy.y.xdx.y.x(
3
x
4
x 22
34
=+++ ∫
La integral que queda pendiente proviene de la derivación de “x2
.y2
”:
C
2
y.x
3
x
4
x 2234
=++
C12y.x6x4x3 2234
=++
Reemplazando “12C” por “k”:

I-2005151
ky.x6x4x3 2234
=++ Solución
0dy).x3y.xe.y.x(dx).yy.x2e.y.x2( 22y423y4
=−−+++
Solución:
Se debe verificar si la ecuación diferencial planteada es exacta.
yy.x2e.y.x2M 3y4
++=
x3y.xe.y.xN 22y42
−−=
y
)yy.x2e.y.x2(
y
M 3y4
∂
++∂
=
∂
∂
Ejecutando las derivadas:
( ) 1y.x6)y4.(ee.yx2
y
M 23yy4
+++=
∂
∂
1y.x6e.y.x8e.y.x2
y
M 2y3y4
+++=
∂
∂
x
)x3y.xe.y.x(
x
N 22y42
∂
−−∂
=
∂
∂
Ejecutando las derivadas:
3y.x2e.y.x2
x
N 2y4
−−=
∂
∂
Debido a que las 2 derivadas parciales no son iguales, la ecuación diferencial no es exacta.
Una inspección de las derivadas parciales cruzadas revela que la diferencia entre las 2
derivadas, dividida para “M” es una función de “y”.
yy.x2e.y.x2
)3y.x2e.y.x2()1y.x6e.y.x8e.y.x2(
M
x
N
y
M
3y4
2y42y3y4
++
−−−+++
=
∂
∂
−
∂
∂
Eliminando paréntesis:
yy.x2e.y.x2
3y.x2e.y.x21y.x6e.y.x8e.y.x2
M
x
N
y
M
3y4
2y42y3y4
++
++−+++
=
∂
∂
−
∂
∂

I-2005152
Simplificando:
yy.x2e.y.x2
4y.x8e.y.x8
M
x
N
y
M
3y4
2y3
++
++
=
∂
∂
−
∂
∂
Factorando:
)1y.x2e.y.x2(y
)1y.x2e.y.x2(4
M
x
N
y
M
2y3
2y3
++
++
=
∂
∂
−
∂
∂
Simplificando:
y
4
M
x
N
y
M
=
∂
∂
−
∂
∂
De donde:
y
4
)y(g =−
y
4
)y(g −=
El factor de integración es:
∫−
=µ dy).y(g
e
Reemplazando la función “g(y)”:
∫−∫−
==µ y
dy
4
y
dy4
ee
)yln(4
e−
=µ
Introduciendo el “-4” en el logaritmo:
)yln( 4
e
−
=µ
)y/1ln( 4
e=µ
Por la relación entre el logaritmo natural y la función exponencial se tiene:
4
y
1
=µ
Multiplicando la ecuación diferencial por el factor de integración se tiene una ecuación
diferencial equivalente:
0
y
dy).x3y.xe.y.x(dx).yy.x2e.y.x2(
4
22y423y4
=
−−+++

I-2005153
0
y
dy).x3y.xe.y.x(
y
dx).yy.x2e.y.x2(
4
22y42
4
3y4
=
−−
+
++
Simplificando:
0dy.
y
x3
y
x
e.xdx.
y
1
y
x
2e.x2
42
2
y2
3
y
=








−−+








++ Ecuación diferencial equivalente
Para la nueva ecuación se deben redefinir las funciones “M” y “N”:
3
y
y
1
y
x
2e.x2M ++=
42
2
y2
y
x3
y
x
e.xN −−=
Obteniendo las derivadas parciales cruzadas:
42
y
y
1
)3(
y
x
)1(2e.x2
y
M
−+−+=
∂
∂
Simplificando:
42
y
y
3
y
x2
e.x2
y
M
−−=
∂
∂
42
y
y
3
y
x2
e.x2
x
N
−−=
∂
∂
Debido a que las 2 expresiones son iguales, la nueva ecuación diferencial es exacta.
Dada la complejidad de expresión de la ecuación diferencial es preferible aprovechar las
expresiones matemáticas relacionadas con la propiedad de ser exacta.
La ecuacióndiferencial básica equivalente es:
0dy.
y
x3
y
x
e.xdx.
y
1
y
x
2e.x2
42
2
y2
3
y
=








−−+








++
3
y
y
1
y
x
2e.x2M ++=
42
2
y2
y
x3
y
x
e.xN −−=
)y(dx).y,x(M)y,x(F
x
φ+= ∫

I-2005154
)y(dx).
y
1
y
x
2e.x2()y,x(F
x
3
y
φ+++= ∫
)y(
y
x
y
x
e.x)y,x(F
3
2
y2
φ+








++= Función primitiva
)y(
y
x
)3(
y
x
)1(e.x
y
F
42
2
y2
φ′+








−+−+=
∂
∂
Simplificando:
)y(
y
x3
y
x
e.x
y
F
42
2
y2
φ′+−−=
∂
∂
Pero:
)y,x(N
y
F
=
∂
∂
De donde:
42
2
y2
42
2
y2
y
x3
y
x
e.x)y(
y
x3
y
x
e.x −−=φ′+−−
Simplificando:
0)y( =φ′
Integrando “φ′ ” se obtiene “φ”, que es una constante:
1k)y( =φ
)y(
y
x
y
x
e.x)y,x(F
3
2
y2
φ+








++=
13
2
y2
k
y
x
y
x
e.x)y,x(F +








++= Función primitiva
k)y,x(F =
kk
y
x
y
x
e.x 13
2
y2
=+








++

Ecuaciones diferenciales de equivalencia 55555

Ecuaciones diferenciales de equivalencia 55555

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (18)

Similar a Ecuaciones diferenciales de equivalencia 55555

Similar a Ecuaciones diferenciales de equivalencia 55555 (20)

Último

Último (15)

Ecuaciones diferenciales de equivalencia 55555