Angulos
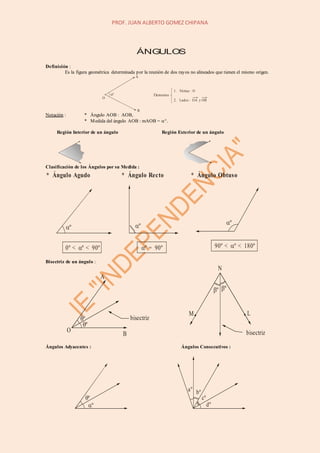
- 1. PROF. JUAN ALBERTO GOMEZ CHIPANA Definición : Es la figura geométrica determinada por la reunión de dos rayos no alineados que tienen el mismo origen. Notación : * Ángulo AOB : AOB, * Medida del ángulo AOB : mAOB = . Región Interior de un ángulo Región Exterior de un ángulo Clasificación de los Ángulos por su Medida : Bisectriz de un ángulo : Ángulos Adyacentes : Ángulos Consecutivos : C ap ít u l o ÁNGULOS 1 º O A B Elementos 1. Vértice : O 2. Lados : OA y OB º 0º < < 90ºº * Ángulo Agudo º = 90ºº * Ángulo Recto º * Ángulo Obtuso 90º < < 180ºº º O A B º bisectriz ºº N M L bisectriz º º aº bº cº dº
- 2. PROF. JUAN ALBERTO GOMEZ CHIPANA Ángulos Adyacentes Suplementarios : Ángulos Opuestos por el vértice º º º º º+ º+ º+ º = 180º Observaciones : º º º º º º+ º+ º+ º+ º = 360º Ángulos Complementarios aº bº aº + bº = 90º Ángulos Suplementarios º + º = 180º º º A C B O Los ángulos AOB y BOC también se les denomina par lineal. A C B O Las bisectrices de todo par lineal son perpendiculares. ºº º º
- 3. PROF. JUAN ALBERTO GOMEZ CHIPANA Observaciones : Es necesariorecordarlossiguientesánguloscomprendidosentrerectasparalelas. º º º º º º º = º º = º º + º = 180º * Alternos Internos * Correspondientes * Conjugados L1 L2 a b c * Si : L1 // L2 L1 L2 aº bº * Si : L1 // L2 xº º+ º+ º+ = aº+ bº+ cº xº = aº + bº
- 4. PROF. JUAN ALBERTO GOMEZ CHIPANA 3 º 120º 2 º 3 º PRÁCTICA DOMICILIARIA 1. Si: esbisectrizdel ánguloAOB,calcule "x°" 2. Calcule "xº". 3. Calcule : 4. Calcule "x°",si : OM 7xº-10º 5xº+ 40º A M B O 4xº+ 20º 3xº+ 50º º 2 L // L1 2 L1 L2 3xº 2xº 80º
- 5. PROF. JUAN ALBERTO GOMEZ CHIPANA L1 L2 4xº 80º 60º 3xº L1 L2 60º xº xº xº B C A O 80º 5. Si : , calcule "x°". 6. Si : , calcule "x°” 7. En el gráfico, las medidas de los ángulos AOB y BOC son suplementarios y la m AOC = 80°. Calcule lam AOB. 8. Si : , calcule : . L // L1 2 L // L1 2 ) ) L //L1 2 ºººº L1 L2 100º º º º º
