CB-101_Ejercicios_semana_11_FB101W.pdf

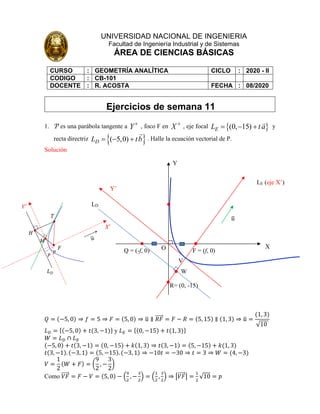
UNIVERSIDAD NACIONAL DE INGENIERIA
Facultad de Ingeniería Industrial y de Sistemas
ÁREA DE CIENCIAS BÁSICAS
CURSO : GEOMETRÍA ANALÍTICA CICLO : 2020 - II
CODIGO : CB-101
DOCENTE : R. ACOSTA FECHA : 08/2020
Ejercicios de semana 11
1. P es una parábola tangente a , foco F en , eje focal y
recta directriz . Halle la ecuación vectorial de P.
Solución
𝑄 = (−5, 0) ⇒ 𝑓 = 5 ⇒ 𝐹 = (5, 0) ⇒ 𝑢
- ∥ 𝑅𝐹
00000⃗ = 𝐹 − 𝑅 = (5, 15) ∥ (1, 3) ⇒ 𝑢
- =
(1, 3)
√10
𝐿! = {(−5, 0) + 𝑡(3, −1)} y 𝐿" = {(0, −15) + 𝑡(1, 3)}
𝑊 = 𝐿! ∩ 𝐿"
(−5, 0) + 𝑡(3, −1) = (0, −15) + 𝑘(1, 3) ⇒ 𝑡(3, −1) = (5, −15) + 𝑘(1, 3)
𝑡(3, −1). (−3, 1) = (5, −15). (−3, 1) ⇒ −10𝑡 = −30 ⇒ 𝑡 = 3 ⇒ 𝑊 = (4, −3)
𝑉 =
1
2
(𝑊 + 𝐹) = B
9
2
, −
3
2
D
Como 𝑉𝐹
00000⃗ = 𝐹 − 𝑉 = (5, 0) − E
#
$
, −
%
$
F = E
&
$
,
%
$
F ⇒ G𝑉𝐹
00000⃗G =
&
$
√10 = 𝑝
Y+
X +
{ }
(0, 15)
E
L t a
= - +
!
{ }
( 5,0)
D
L tb
= - +
!
X
Y
O F = (f, 0)
Q = (-f, 0)
LE (eje X’)
LD
R= (0, -15)
Y’
V
W
𝑢
-

𝒫 = JB
9
2
, −
3
2
D + 𝑥'
(1, 3)
√10
+ 𝑦'
(−3, 1)
√10
𝑦'$
M = 2√10𝑥′O
2. Sea P una parábola con eje focal de pendiente positiva. y
son los extremos de una cuerda focal de P. Si las rectas tangentes a P en M y N se
interceptan en un punto de , halle la ecuación vectorial de P.
Solución
Como:
𝑄𝑀
000000⃗ ⊥ 𝑄𝑁
000000⃗ ⇒ 𝑄𝑀
000000⃗. 𝑄𝑁
000000⃗ = 0 ⇒ (4, −4 − 𝑦). (14, 11 − 𝑦) = 0
56 − (4 + 𝑦)(11 − 𝑦) = 0 ⇒ 56 − 44 − 7𝑦 + 𝑦$
⇒ 𝑦$
− 7𝑦 + 12 = 0
𝑦 = 3, 𝑦 = 4
Sea R punto medio de 𝑀𝑁
----- esto es:
𝑅 =
1
2
(𝑀 + 𝑁) =
1
2
(18, 7) = B9,
7
2
D
Por propiedad 𝑄𝑅
00000⃗ ∥ al eje focal (*)
Si 𝑦 = 4 ⇒ 𝑄 = (0, 4) ⇒ 𝑄𝑅
00000⃗ = E9, −
&
$
F no cumple (*)
Si 𝑦 = 3 ⇒ 𝑄 = (0, 3) ⇒ 𝑄𝑅
00000⃗ = E9,
&
$
F sí cumple (*)
(4, 4)
M = - (14,11)
N =
Y+
X
Y
O
LN
LM
N = (14, 11)
M = (4, -4)
Q = (0, y)
F
R
V
X’
Y’
𝑢
-
(
2
,
3
)
𝐿!

𝑢
- =
1
5√13
(18, 1)
De la figura:
𝑄𝑁
000000⃗ = 𝑄𝐹
00000⃗ + 𝐹𝑁
00000⃗ ⇒ (14, 8) = 𝑟(3, −2) + 𝑘(2, 3)
(14, 8). (−3, 2) = 𝑟(3, −2). (−3, 2) ⇒ 𝑟 = 2 ⇒ 𝑄𝐹
00000⃗ = (6, −4) ⇒ 𝐹 = (6, −1)
Por otro lado:
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝑄𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(&+,&)(6, −4) =
1
2
(6, −4). (18, 1)
325
(18, 1) =
4
25
(18, 1)
⇒ 𝑝 =
4
5
√13, 𝑉 = B
78
25
, −
29
25
D
Luego la ecuación vectorial de 𝒫 es:
𝒫 = XB
78
25
, −
29
25
D + 𝑥'
1
5√13
(18, 1) + 𝑦'
1
5√13
(−1, 18) 𝑦
M ′$
=
16
5
√13𝑥′Y
3. Sea P una parábola con foco eje focal , y la
recta directriz . Si es tangente a P en T. Halle la ecuación
vectorial de P y las coordenadas del punto T.
Solución
Como 𝑅𝐹
00000⃗ ⊥ 𝑅𝑄
00000⃗ ⇒ (𝑓 + 3, 4). (−𝑓 + 3, 4) = 0 ⇒ −𝑓$
+ 9 + 16 = 0 ⇒ 𝑓 = 5
𝐹 = (5, 0) ⇒ 𝑅𝐹
00000⃗ = (8, 4) ⇒ 𝑉𝐹
00000⃗ = (4, 2) ⇒ 𝑉 = (1, −2), 𝑝 = 2√5, 𝑢
- =
(2, 1)
√5
Luego la ecuación de la parábola es:
𝒫 = J(1, −2) + 𝑥'
(2, 1)
√5
+ 𝑦'
(−1, 2)
√5
𝑦'$
M = 8√5𝑥′O
Además 𝐿 = {(−5, 0) + 𝑡(2, 1)}
,
F X +
Î ( ) ( )
{ }
3, 4 1,
E
L t m
= - - + 0
m >
( ) ( )
{ }
3, 4 ,1
D
L t m
= - - + - Y +
X
Y
O F = (f, 0)
(-f, 0) = Q
X’
Y’
LD
V
(-3, -4) = R
T L

Como 𝑇 = 𝐿 ∩ 𝑌 ⇒ (−5, 0) + 𝑡(2, 1) = (0, 𝑦) ⇒ 𝑦 = 5/2
⇒ 𝑇 = B0,
5
2
D
4. Sea P = una parábola con foco F = (5, 5), que pasa
por el punto Q = (10, 20) y eje focal de pendiente positiva. es una circunferencia con
diámetro . Si es un punto del eje , halle la ecuación vectorial de P.
Solución
𝒫 = J(2, 4) + 𝑥′
(3, 1)
√10
+ 𝑦′
(−1, 3)
√10
𝑦'$
M = 4√10𝑥′O
De la figura:
𝐶 =
1
2
(𝐹 + 𝑄) = B
15
2
,
25
2
D
𝐹𝑄
00000⃗ = 𝑄 − 𝐹 = (5, 15) = 5(1, 3)
𝑟 =
1
2
G𝐹𝑄
00000⃗G =
5
2
√10 … (1)
También:
𝑇 ∈ 𝑌.
⇒ 𝑇 = (0, 𝑡), 𝑡 > 0
Luego:
𝑇𝐶
00000⃗ = 𝐶 − 𝑇 = B
15
2
,
25
2
− 𝑡D
Como:
G𝑇𝐶
00000⃗G = 𝑟 … (2)
Reemplazar (1) en (2):
G𝑇𝐶
00000⃗G =
5
2
√10 ⇒ aB
15
2
,
25
2
− 𝑡Da =
5
2
√10 ⇒ aB3, 5 −
2
5
𝑡Da = √10
⇒ 9 + B5 −
2
5
𝑡D
$
= 10 ⇒ B5 −
2
5
𝑡D
$
= 1 ⇒ 𝑡 = 10, 𝑡 = 15
Para:
𝑡 = 15 ⇒ 𝑇𝐶
00000⃗ = B
15
2
, −
5
2
D ∥ (3, −1) (𝑛𝑜 𝑐𝑢𝑚𝑝𝑙𝑒)
𝑡 = 10 ⇒ 𝑇𝐶
00000⃗ = B
15
2
,
5
2
D ∥ (3, 1) (𝑐𝑢𝑚𝑝𝑙𝑒)
Luego:
𝑢
- =
(3, 1)
√10
, 𝑇 = (0, 10)
Como:
𝑇𝐹
00000⃗ = 𝐹 − 𝑇 = (5, −5)
𝑉𝐹
00000⃗ = 𝑝𝑟𝑜𝑦(
)𝑇𝐹
00000⃗ = 𝑝𝑟𝑜𝑦(%,&)(5, −5) =
(5, −5). (3, 1)
10
(3, 1)
𝑉𝐹
00000⃗ = (3, 1) ⇒ 𝑝 = √10, 𝐹 − 𝑉 = (3, 1) ⇒ 𝑉 = (2, 4)
Luego la ecuación vectorial de la parábola es:
2
{ / 4 }
v x u y u y px
^
¢ ¢ ¢ ¢
+ + =
z
FQ
!!!
"
Y
z ¢
Ç Y+
Q = (10, 20)
F = (5, 5)
X’
Y’
T
C
V
r
r
r
𝑢
-

𝒫 = J(2, 4) + 𝑥′
(3, 1)
√10
+ 𝑦′
(−1, 3)
√10
𝑦'$
M = 4√10𝑥′O
5. Sea P una parábola con foco F = (6, 1), eje focal con pendiente y recta
directriz . es una recta tangente a P en T ( T en el primer
cuadrante). Si , halle la ecuación vectorial de P.
Solución
𝒫 = J(5, 0) + 𝑥′
(1,1)
√2
+ 𝑦′
(−1,1)
√2
𝑦'$
M = 4√2𝑥′O
Como:
𝐿/ = {(3, 5) + 𝑡(1, 2)}
𝐿/: (𝑥 − 3, 𝑦 − 5). (−2, 1) = 0
𝐿/ : − 2𝑥 + 𝑦 + 1 = 0
Luego:
𝑑(𝐹, 𝐿/) =
|−2(6) + 1 + 1|
√5
= 2√5
⇒ 𝐹𝐻
00000⃗ = 4√5
(−2, 1)
√5
= (−8, 4)
⇒ 𝐻 − 𝐹 = (−8, 4) ⇒ 𝐻 = (−2, 5)
Como:
𝑇 ∈ 𝐿/
⇒ 𝑇 = (3, 5) + 𝑡(1, 2)
⇒ 𝑇 = (3 + 𝑡, 5 + 2𝑡)
Además:
𝐻𝑇
00000⃗ = 𝑇 − 𝐻 = (5 + 𝑡, 2𝑡)
Pero: G𝐻𝑇
00000⃗G = 10√2
⇒ |(5 + 𝑡, 2𝑡)| = 10√2 ⇒ (5 + 𝑡)$
+ 4𝑡$
= 0200
⇒ 5𝑡$
+ 10𝑡 − 175 = 0 ⇒ 𝑡$
+ 2𝑡 − 35 = 0 ⇒ 𝑡 = 5, 𝑡 = −7
Para:
𝑡 = −7 ⇒ 𝑇 = (−4, −9) (No cumple pues T no está en el primer cuadrante)
𝑡 = 5 ⇒ 𝑇 = (8, 15) (Cumple, pues T esta en el primer cuadrante)
⇒ 𝐻𝑇
00000⃗ = (10, 10)
Luego:
𝑢
- =
(1, 1)
√2
Además:
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(&,&)(8, −4) =
1
2
(8, −4). (1, 1)
2
(1, 1)
⇒ 𝑉𝐹
00000⃗ = (1, 1) ⇒ 𝑝 = √2, 𝐹 − 𝑉 = (1, 1) ⇒ 𝑉 = (5, 0)
𝒫 = J(5, 0) + 𝑥′
(1,1)
√2
+ 𝑦′
(−1,1)
√2
𝑦'$
M = 4√2𝑥′O
(0 2)
m m
< <
D
L { }
(3,5) (1,2)
T
L t
= +
( , ) 10 2
D
d T L =
X’
Y’
V
F = (6, 1)
𝐿!
H M
𝐿/
T
10√2
10√2
(
1
,
2
)
𝑢
-

6. Sea P una parábola con foco F = (4, 0), directriz D, eje focal con pendiente positiva.
es una recta tangente a P, si donde .
Halle la ecuación vectorial de P .
Solución
𝒫 = J(3, −2) + 𝑥′
(1,2)
√5
+ 𝑦′
(−2,1)
√5
𝑦'$
M = 4√5𝑥′O
De la figura:
tan(𝜃) =
3
4 −
2
11
1 + E
3
4F E
2
11F
=
1
2
… (1)
Pero:
tan(𝜃) =
𝑚0/ −
3
4
1 + 𝑚0/ E
3
4F
… (2)
Reemplazar (1) en (2):
1
2
=
𝑚0/ −
3
4
1 + 𝑚0/ E
3
4F
=
4𝑚0/ − 3
4 + 3𝑚0/
⇒ 𝑚0/ = 2 ⇒ 𝑢
- =
(1, 2)
√5
Como:
G𝐹𝑀
000000⃗G = 𝑑(𝐹, 𝐿/) =
|25|
5
= 5 ⇒ 𝑀𝐹
000000⃗ = 5
(−3, 4)
5
= (−3, 4)
Además:
𝑉𝐹
00000⃗ = 𝑝𝑟𝑜𝑦(
)𝑀𝐹
000000⃗ = 𝑝𝑟𝑜𝑦(&,$)(−3, 4) =
(−3, 4). (1, 2)
5
(1, 2)
𝑉𝐹
00000⃗ = (1, 2) ⇒ 𝑝 = √5, 𝐹 − 𝑉 = (1, 2) ⇒ 𝑉 = (3, −2)
𝒫 = J(3, −2) + 𝑥′
(1,2)
√5
+ 𝑦′
(−2,1)
√5
𝑦'$
M = 4√5𝑥′O
:3 4 37 0
T
L x y
- - = //( 2,11)
QF -
!!!"
T
Q L D
Î Ç
X’
Y’
F = (4, 0)
D
Q
T
𝐿/
V
(4, 3)
(-
2
,
1
1
)
(11, 2)
H
𝜃
𝜃
M
𝑢
-

7. Una parábola P es tangente al eje Y en y al eje X en T, si es
un punto de la directriz, halle la ecuación vectorial de P.
Solución
𝒫 = JB4,
1
2
D + 𝑥′
(1, 2)
√5
+ 𝑦′
(−2, 1)
√5
𝑦'$
M = 4√5𝑥′O
De la gráfica:
𝑢
-1
∥ (2, −1) ⇒ 𝑢
- =
(1, 2)
√5
Como:
𝐿! = {𝑡(2, −1)}
⇒ 𝐿!: (𝑥, 𝑦). (1, 2) = 0
⇒ 𝐿!: 𝑥 + 2𝑦 = 0
Luego:
𝑑(𝑄, 𝐿!) =
|25|
√5
= 5√5
⇒ 𝐻𝑄
000000⃗ = 5√5
(1, 2)
√5
= (5, 10)
𝑄 − 𝐻 = (5, 10) ⇒ 𝐻 = B−5,
5
2
D
Como H y F son simétricos respecto el eje Y, entonces:
𝐹 = B5,
5
2
D
Como:
𝐻𝐹
00000⃗ = 𝐹 − 𝐻 = (10, 0)
⇒ 𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(&,$)(10, 0) =
1
2
(10, 0). (1, 2)
5
(1, 2)
⇒ 𝑉𝐹
00000⃗ = (1, 2) ⇒ 𝑝 = √5, 𝐹 − 𝑉 = (1, 2) ⇒ 𝑉 = B4,
1
2
D
𝒫 = JB4,
1
2
D + 𝑥′
(1, 2)
√5
+ 𝑦′
(−2, 1)
√5
𝑦'$
M = 4√5𝑥′O
25
0,
2
Q
æ ö
= ç ÷
è ø
5
5,
2
E
æ ö
= -
ç ÷
è ø
X
Y
B0,
25
2
D = 𝑄
O
𝐿!
𝐸 = B5, −
5
2
D
𝑢
-1
T
F
X’
V
𝑢
-
H M

8. Una Parábola P con foco F = (0, 0), tiene su vértice en el IV cuadrante. El eje X intercepta
a P en los puntos M = (-10, 0) y N. La recta es tangente a P en el
punto N. Halle la ecuación vectorial de P.
Solución
Como:
𝑄𝑀
000000⃗. 𝑄𝑅
00000⃗ = 0 ⇒ (−10, 𝑦). (4, −3 + 𝑦) = 0 ⇒ −40 − 3𝑦 + 𝑦$
= 0 ⇒ 𝑦 = 8, 𝑦 = −5
𝑄 = (0, −8) ⇒ 𝑀𝑄
000000⃗ = 𝑄 − 𝑀 = (10, −8)
⇒ 0𝐿23 = {(−10, 0) + 𝑡(5, −4)} ⇒ 𝐿23: (𝑥 + 10, 𝑦). (4, 5) = 0
𝐿23: 4𝑥 + 5𝑦 + 40 = 0
𝑑p𝐹, 𝐿23q =
|40|
√41
=
40
√41
⇒ 𝐻 = 𝐹 +
80
√41
(−4, −5)
√41
= B−
320
41
. −
400
41
D
𝐻𝑀
0000000⃗ = 𝑀 − 𝐻 = (−10, 0) − B−
320
41
. −
400
41
D = B−
90
41
,
400
41
D ∥ (−9, 40)
𝑢
0⃗ =
(−9, 40)
41
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
E
320
41 .
400
41 F . (−9, 40)
41$
(−9, 40) =
160
41$
(−9, 40)
𝑉 = −
160
41$
(−9, 40), 𝑝 =
160
41
{ }
(4, 3)
L t a
= - +
!
Q = (0, - y)
F
X
Y
(-10, 0) = M N
L
R = (4, - 3)
LD
X’
H
V

𝒫 = J−
160
41$
(−9, 40) + 𝑥′
(−9, 40)
41
+ 𝑦′
(−40, −9)
41
∕ 𝑦′$
= 4 B
160
41
D 𝑥′O
9. Una parábola P con foco es tangente al eje en el punto y la
recta es tangente a P en el punto T. Halle las coordenadas de
T.
Solución
𝒫 = JB−
1
2
,
1
2
D + 𝑥′
(−1, 1)
√2
+ 𝑦′
(−1, 1)
√2
𝑦'$
M = 2√2𝑥′O
𝑇 = (−8, 2)
Como:
𝐿 = {(−4, 0) + 𝑡(2, −1)}
⇒ 𝐿: (𝑥 + 4, 𝑦). (1, 2) = 0
⇒ 𝐿: 𝑥 + 2𝑦 + 4 = 0
Luego:
𝑑(𝐹, 𝐿) =
|−1 + 2 + 4|
√5
= √5
⇒ 𝐹𝐻
00000⃗ = 2√5
(−1, −2)
√5
= (−2, −4) ⇒ 𝐻 − 𝐹 = (−2, −4) ⇒ 𝐻 = (−3, −3)
𝐿! ∥ 𝐻𝑅
000000⃗ = 𝑅 − 𝐻 = (2, 2) ⇒ 𝑢
- =
(−1, 1)
√2
La ecuación de la recta que pasa por T y H es:
𝐿/0 = {(−3, −3) + 𝑟(1, −1)}
Como: 𝑇 = 𝐿 ∩ 𝐿/0:
(−4, 0) + 𝑡(2, −1) = (−3, −3) + 𝑟(1, −1)
⇒ 𝑡(2, −1) = (1, −3) + 𝑟(1, −1) ⇒ 𝑡(2, −1). (1, 1) = (1, −3). (1, 1)
⇒ 𝑡 = −2 ⇒ 𝑇 = (−4, 0) − 2(2, −1) ⇒ 𝑇 = (−8, 2)
( 1,1)
F - X -
( 2,0)
A -
{ }
( 4,0) (2, 1)
L t
= - + -
X
Y
O
F = (-1, 1)
A=(-2, 0)
Q=(-4, 0)
𝐿
(2, -1)
R = (-1, -1)
H
𝐿!
X’
𝑢
-
T

9.1.Una parábola P con foco es tangente al eje en el punto y la
recta es tangente a P en el punto T. Halle las coordenadas de
T.
Solución
De la figura:
tan(𝜃) =
1 −
1
3
1 +
1
3
=
1
2
=
1
3 − 𝑚/4
1 +
1
3 𝑚/4
⇒ 𝑚/4 = −
1
7
⇒ 𝐿/4 = {(−1, 1) + 𝑟(7, −1)}
Luego:
𝑇 = 𝐿/4 ∩ 𝐿
(−1, 1) + 𝑟(7, −1) = (−4, 0) + 𝑡(2, −1) ⇒ 𝑟(7, −1) = (−3, −1) + 𝑡(2, −1)
⇒ 𝑟(7, −1). (1, 2) = (−3, −1). (1, 2) ⇒ 𝑟 = −1 ⇒ 𝑇 = (−1, 1) − (7, −1) = (−8, 2)
𝒫 = JB−
1
2
,
1
2
D + 𝑥′
(−1, 1)
√2
+ 𝑦′
(−1, 1)
√2
𝑦'$
M = 2√2𝑥′O
𝑇 = (−8, 2)
( 1,1)
F - X -
( 2,0)
A -
{ }
( 4,0) (2, 1)
L t
= - + -
X
Y
𝐴(−2, 0)
𝑄(−4, 0)
𝐹(−1, 1)
𝐿
(2, −1)
𝑇
𝜃
𝜃

10. Sea P una parábola con vértice V y foco F = (5, 5). es una recta
tangente a P en T = (30, 5). Halle la ecuación de P.
Solución
De la figura:
𝐹𝑇
00000⃗ = 𝑇 − 𝐹 = (25, 0) ∥ (1, 0)
Como:
𝐿/ ∥ (2, 1) ⇒ tan(𝜃) =
1
2
=
𝑚0/ −
1
2
1 +
1
2 𝑚0/
⇒ 𝑚0/ =
4
3
⇒ 𝐻𝑇
00000⃗ ∥ (3,4) ⇒ 𝑢
- =
(3, 4)
5
Como:
𝐻𝐹
00000⃗ = 𝐻𝑇
00000⃗ + 𝑇𝐹
00000⃗ ⇒ 𝑟(−1, 2) = 𝑥(3, 4) + (−25, 0)
⇒ 𝑟(−1, 2). (−4, 3) = (−25, 0). (−4, 3) ⇒ 𝑟 = 10 ⇒ 𝐻𝐹
00000⃗ = (−10, 20)
Luego:
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(%,5)(−10, 20) =
1
2
(−10, 20). (3, 4)
25
(3, 4)
𝑉𝐹
00000⃗ = (3, 4) ⇒ 𝑝 = 5; 𝐹 − 𝑉 = (3, 4) ⇒ 𝑉 = (2, 1)
𝒫 = J(2, 1) + 𝑥′
(3, 4)
5
+ 𝑦′
(−4, 3)
5
𝑦'$
M = 20𝑥′O
{ }
(2,1)
T
L Q t
= +
𝐿/
𝐿!
𝐹 = (5, 5) 𝑇 = (30, 5)
𝐻
(2,1)
𝜃
𝜃
𝑋′
𝑌′
𝑉
𝑢
-
(1, 0)

11. Sea P una parábola con vértice V, foco F = (5, 5) y eje focal de pendiente positiva. Si
y = (30, 5) pertenecen a P , halle la ecuación vectorial de P.
Solución
De la figura:
𝑄 =
1
2
(𝑃& + 𝐹) = (1, 8)
⇒ 𝑄𝐹
00000⃗ = 𝐹 − 𝑄 = (4, −3)
⇒ 𝑟& = 5
𝑅 =
1
2
(𝐹 + 𝑃$) = B
35
2
, 5D
⇒ 𝐹𝑅
00000⃗ = 𝑅 − 𝐹 = B
25
2
, 0D ⇒ 𝑟$ =
25
2
Además:
𝑄𝑅
00000⃗ = 𝑅 − 𝑄 = B
33
2
, −3D ∥ (11, −2), G𝑄𝑅
00000⃗G =
15√5
2
Como:
G𝐻𝑅
000000⃗G = 𝑟$ − 𝑟& =
25
2
− 5 =
15
2
⇒ G𝑄𝐻
000000⃗G = 15 ⇒ tan(𝜃) =
G𝐻𝑅
000000⃗G
G𝑄𝐻
000000⃗G
=
1
2
Luego:
1
2
=
−
2
11 − 𝑚30
1 + (−
2
11)𝑚30
⇒ 𝑚30 = −
3
4
⇒ 𝑢
- =
(3, 4)
5
También de la figura:
𝑇𝑄
00000⃗ = 5
(3, 4)
5
= (3, 5) ⇒ 𝑄 − 𝑇 = (3, 4) ⇒ 𝑇 = (−2, 4)
⇒ 𝑇𝐹
00000⃗ = 𝐹 − 𝑇 = (5, 5) − (−2, 4) = (7, 1)
⇒ 𝑉𝐹
00000⃗ = 𝑝𝑟𝑜𝑦(
)𝑇𝐹
00000⃗ = 𝑝𝑟𝑜𝑦(%,5)(7, 1) =
(7, 1). (3, 4)
25
(3, 4) = (3, 4)
⇒ 𝑉𝐹
00000⃗ = (3, 4) ⇒ 𝑝 = 5; 𝐹 − 𝑉 = (3, 4) ⇒ 𝑉 = (2, 1)
Así obtenemos la ecuación de la parábola:
𝒫 = J(2, 1) + 𝑥′
(3, 4)
5
+ 𝑦′
(−4, 3)
5
𝑦'$
M = 20𝑥′O
1 ( 3,11)
P = - 2
P
𝐹(5, 5)
𝑃$(30, 5)
𝑃&(−3, 11)
𝑌′
𝑋′
𝑉
𝑄
𝑅
𝑟&
𝑟$
𝐻
𝜃
𝑢
-
𝑇

12. P es una parábola con foco F = (5, -2), es tangente a P en T. Si es una cuerda
focal de P con , . Halle la ecuación vectorial de P.
Solución
De la figura:
𝐻𝑄
000000⃗ = 𝑄 − 𝐻 = B5,
5
2
D ∥ 𝑢
-1
𝑢
- =
(1, −2)
√5
Como:
𝐻𝐹
00000⃗ = (10, 0)
⇒ 𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗
⇒ 𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(&,6$)(10, 0)
⇒ 𝑉𝐹
00000⃗ = (1, −2)
⇒ 𝑝 = √5
⇒ 𝐹 − 𝑉 = (1, −2) ⇒ 𝑉 = (4, 0)
𝒫 = J(4, 0) + 𝑥′
(1, −2)
√5
+ 𝑦′
(2, 1)
√5
𝑦'$
M = 4√5𝑥′O
-
Y TR
÷
ø
ö
ç
è
æ
=
2
1
,
r
R 0
>
r
X
Y
𝑇(0, −𝑦)
𝑅 B𝑟,
1
2
D
𝐹(5, −2)
𝐻(−5, −2)
𝑄 B0,
1
2
D
𝐿!
X’
Y’
𝑉

12.1. P es una parábola con foco F = (5, -2), es tangente a P en T. Si es una
cuerda focal de P con , . Halle la ecuación vectorial de P.
Solución
De la figura:
𝐻𝑄
000000⃗ = 𝑄 − 𝐻 = B0,
1
2
D − (−5, −2) = B5,
5
2
D ∥ (2, 1) ⇒ 𝑢
- =
(1, −2)
√5
Luego:
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(&,6$)(10, 0) =
1
2
(10, 0). (1, −2)
5
(1, −2)
⇒ 𝑉𝐹
00000⃗ = (1, −2) ⇒ 𝑝 = √5; 𝐹 − 𝑉 = (1, −2) ⇒ 𝑉 = (4, 0)
𝒫 = J(4, 0) + 𝑥′
(1, −2)
√5
+ 𝑦′
(2, 1)
√5
𝑦'$
M = 4√5𝑥′O
-
Y TR
÷
ø
ö
ç
è
æ
=
2
1
,
r
R 0
>
r
𝑅 B𝑟,
1
2
D
𝑌
𝑋
𝐹(5, −2)
𝑇
𝑄 B0,
1
2
D
𝐻(−5, −2)
𝑋′
𝑢
-
𝑌′
𝑉

13. P es una parábola de vértice V en el IV cuadrante, foco F en , eje focal con pendiente
positiva, el eje Y es tangente a P en , L es una recta tangente a P en Q tal que
L determina con el eje focal de P un ángulo de 45º y , halle la ecuación
vectorial de P.
Solución
De la figura:
tan(𝜃) = 2 ⇒ tan(𝛼) =
1
2
⇒ 𝑢
- =
(2, 1)
√5
Como:
𝐻𝑇
00000⃗ ∥ 𝑢
- ⇒ B𝑓,
5
4
D ∥ (2, 1) ⇒
5
4𝑓
=
1
2
⇒ 𝑓 =
5
2
⇒ 𝐹 = B
5
2
, 0D , 𝐻 = B−
5
2
, 0D
⇒ 𝐻𝐹
00000⃗ = 𝐹 − 𝐻 = (5, 0)
Luego:
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦($,&)(5, 0) =
1
2
(5, 0). (2, 1)
5
(2, 1)
⇒ 𝑉𝐹
00000⃗ = (2, 1) ⇒ 𝑝 = √5; 𝐹 − 𝑉 = (2, 1) ⇒ 𝑉 = B
1
2
, −1D
Por lo tanto la ecuación vectorial de la parábola es:
𝒫 = JB
1
2
, −1D + 𝑥′
(2, 1)
√5
+ 𝑦′
(−1, 2)
√5
∕ 𝑦'$
= 4√5𝑥′O
X +
5
0,
4
T
æ ö
= ç ÷
è ø
/ /(0,1)
QV
!!!"
𝑋
𝑌
𝐹 = (𝑓, 0)
𝑇 = B0,
5
4
D
𝐻 = (−𝑓, 0)
𝑋′
𝑉
𝑄
45°
𝐿
45° 45°
𝐿!
𝑝
𝑝
2𝑝
𝜃
(0, 1)
𝑢
-
𝛼

14. P es una parábola con eje focal de pendiente positiva cuyo foco es el origen de
coordenadas tal que P. La recta es tangente a
P en , halle la ecuación vectorial de P.
Solución
𝒫 = JB−
8
5
, −
6
5
D + 𝑥′
(4, 3)
5
+ 𝑦′
(−3, 4)
5
𝑦'$
M = 8√5𝑥′O
15. y son rectas tangentes
a una parábola P de foco F, directriz , en los puntos Q y T respectivamente,
, , , , 0 , , halle la
ecuación vectorial de P.
16. P es una parábola con foco F, vértice V, eje focal y recta
directriz , es una recta tangente a P en T = (-1, 9). Si
. Halle la ecuación vectorial de P.
Solución
𝒫 = J(3, 2) + 𝑥′
(2, 3)
√13
+ 𝑦′
(−3, 2)
√13
𝑦'$
M = 4√13𝑥′O
17. Sea P una parábola con vértice V = (2, 1) y foco F. Sea una circunferencia de centro
C = (19,- 2) de forma que . Si , y eje focal
, . Halle la ecuación vectorial de P.
18. P es una parábola con foco F , recta directriz LD de pendiente negativa, el eje Y es
tangente a P e intercepta LD en el punto E, , LT es tangente a P en un punto
del primer cuadrante, LT intercepta a LD en el punto G, , , halle la
pendiente de la recta LT.
Solución
𝑚 = −
1
3
19. P es una parábola de foco F, recta directriz con pendiente negativa, vértice V,
, y son puntos de P y del eje focal respectivamente
tal que , , , , , A es
un punto de y , D es un punto tal que , y
halle la ecuación vectorial de P .
(0,10)
M = Î { }
(3, 4)
L t a
= - +
(0, )
E e
=
{ }
1 (5,6) (1, )
L t m
= + tÎ! { }
2 (9,13) (4,7)
L r
= + r Î!
D
L 2 m
<
( 6,3)
A = - Î D
L D
TA L
^
!!"
/ /(1, )
TA n
!!"
1
n
< < (6, 2)
E = - FQ
Î
{ }
(7,8) (1, )
L t m
= + 0
m >
{ }
( 5,3) ( ,1)
D
L r m
= - + - T
L
2
FT VF
=
!!!
" !!!
"
z
{ } (18,1)
P P
z Ç = = (1,0) 0
comp VF >
!!!
"
{ }
(1, )
L F t m
= + 2
m <
(5,10)
EF =
!!!
"
(2,1)
GF r
=
!!!"
0
r >
D
L
(1,0) 0
comp VF >
!!!
"
C (20,0)
B = E
L
. 0
CB FB =
!!!
" !!!
"
(2,11)
FC k
=
!!!
"
0
k > 0
VF
comp FC >
!!!
"
!!!
"
0
VF
comp FC
^ >
!!!
"
!!!
"
D
L E
L . 0
AD DB =
!!!" !!!
"
(8, 6)
AD = -
!!!"
10
DF =
!!!"

20. P es una parábola con vértice , , foco F(0, 0),
es tangente a P en N = (0, ), . El punto M(0, 10) es un
punto de P, halle la ecuación vectorial de P.
21. Los puntos (10, 0) y (0, -5) pertenecen a una parábola P con foco F = (0, 0) y vértice V
en el segundo cuadrante. Halle la ecuación vectorial de P.
Solución
𝒫 = JB−
4
5
,
3
5
D + 𝑥′
(4, −3)
5
+ 𝑦′
(3, 4)
5
𝑦'$
M = 4𝑥′O
22. Sea P una parábola con foco , vértice V, recta directriz y eje focal con
pendiente mayor que 1, es tangente a P. Sea L una recta tal que
, P y , si . Halle la ecuación vectorial
de P.
Solución
De la figura:
tan(45°) = 1 =
𝑚7' −
1
7
1 + (𝑚7!) E
1
7F
⇒ 1 =
7𝑚7' − 1
7 + 𝑚7'
⇒ 𝑚7' =
4
3
⇒ 𝑢
- =
(3, 4)
5
Por otra parte:
𝑑(𝐹, 𝐿/) =
|7(5) + 5 + 10|
5√2
= 5√2
𝐻 = 𝐹 + 10√2
(−7, −1)
5√2
= (5, 5) + (−14, −2) = (−9, 3)
𝐻𝐹
00000⃗ = 𝐹 − 𝐻 = (14, 2)
⇒ 𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(%,5)(14, 2) =
1
2
(14, 2). (3, 4)
25
(3, 4)
( , ) , 0
v h k h < 0
k <
{ }
(3, 4)
T
L t a
= - +
!
n 0
n <
(5,5)
F = D
L
:7 10 0
T
L x y
+ + =
D
Q L L
= Ç { }
,
V R L
= Ç / / (7,1)
L 5 QV QR
=
!!!
"
!!!#
𝐿/
𝐹 = (5, 5)
𝐻
𝐿
𝑇
𝑉
(7, 1)
(−1, 7)
𝐿!
𝑄
𝑅
𝑋′
𝑝
3𝑝
5𝑝
𝑊
𝑝
4𝑝
𝑀
45
4𝑝

𝑉𝐹
00000⃗ = (3, 4) ⇒ 𝑝 = 5; 𝐹 − 𝑉 = (3, 4) ⇒ 𝑉 = (2, 1)
𝒫 = J(2, 1) + 𝑥′
(3, 4)
5
+ 𝑦′
(−4, 3)
5
𝑦'$
M = 4𝑥′O
23. P es una parábola con foco F en el eje , vértice y punto de paso .
La recta L es tangente a P en T y corta al eje focal de P en A.
es un punto de la directriz tal que , , si (6,0) P. Halle la
24. En una parábola P el eje es tangente a P en el vértice V, es una recta
tangente a P en T un punto del primer cuadrante, B(1, -4) es un punto de P, Halle la
ecuación de P.
25. y son dos circunferencias secantes en E y F en el que centro de es un
punto de , y . Se trazan diámetro de
y diámetro de tal que D = (0, 10) , , y
. es el eje focal de la parábola P con foco F, vértice V,
tal que , , . Si D es un punto de la
recta directriz de P y P, halle la ecuación vectorial de P.
26. P es una parábola con eje focal de pendiente positiva, foco F = (f, 0), f > 0, recta
directriz donde . es recta tangente a P en
T un punto del I cuadrante e intercepta a en el punto A del III cuadrante, donde
E = (0, f), . es una recta que intercepta a 𝐿/ en el punto B del
III cuadrante, y . Si en la prolongación de se ubica el punto G tal
que y , halle la ecuación de la reta 𝐿&.
27. P es una parábola cuyo eje focal tiene pendiente positiva, foco F y vértice V,
P es un punto de P tal que y la recta
interseca a la directriz de P en el punto H = (13, -2) donde (eje focal de P). Sea
Q un punto de 𝐹𝑃 y N un punto de 𝐹𝐻 tal que 𝑁𝑄
000000⃗ = (−3,6). Si 𝑁𝑄 𝑃𝐹 y 𝑁𝐹 =
5√2 , halle la ecuación vectorial de P.
28. Sea 𝐿 = {𝑄 + 𝑡 } una recta que pasa por el vértice V y el punto P = (7, 13) de una
parábola P, la recta 𝐿! = {𝑁 + 𝑟(1, 𝑚)}, 𝑚 < 0 es directriz de P ,
𝐿! ∩ 𝐿 = 𝐵 = (2, −2). Si G𝐵𝑉
00000⃗G = √10 , halle la ecuación vectorial de P .
Solución
𝒫 = J(3, 1) + 𝑥′
(2, 1)
√5
+ 𝑦′
(−1, 2)
√5
𝑦'$
M = 4√5𝑥′O
X V e Y - T e X -
Q ˆ ˆ
2
QAF QFA
= QT TF
=
!!!
" !!!
"
Î
Y -
{ }
(2,1)
T
L t
=
1
C 2
C 1
C
2
C (1,0) 0
comp EF >
!!!
"
(0,1) 0
comp EF <
!!!
"
DF
1
C FP 2
C (1,2)
FP t
=
!!!
"
0 15
t
< <
DF FP
<
!!!" !!!
"
{ }
E
L Q tu
= +
!
0
VF
comp FP
^ >
!!!
"
!!!
"
2
(26,8)
Q C
= Î (12,21)
VP =
!!"
D
L PÎ
E
L
{ }
D
L tb
=
!
{ }
D E
L L D
Ç = { }
T
L E t a
= +
!
E
L
DE EF
=
!!!
" !!!
"
1 { }
L tc
=
!
1 { }
L FT C
Ç = BC
m TCG a
=
!
2
3
tga =
(1,0) 0,
comp VF >
!!!
"
10 5
PF =
!!!
"
{ }
L P t a
= +
!
/ / E
L L
^
a

29. P es una parábola con foco F = (0, 0) y eje focal ,
M = (0, 10) P y la recta es tangente a P en , halle la
{ (1, )}
E
L F t m
= + 0
m >
Î {(3, 4) }
T
L t a
= - + T Y
Î

30. P es una parábola con foco F, eje focal de pendiente positiva tal que ,
es tangente a P en T, donde (0,10) .
es tangente a P en . Halle la ecuación vectorial de P.
Solución
De la figura:
𝐹𝑀
000000⃗ = 𝑀 − 𝐹 = (𝑓, 10) ∥ B1,
10
𝑓
D … (1)
𝐹𝑄
00000⃗ = 𝑄 − 𝐹 = (𝑓 − 12, −4) ∥ B1,
−4
𝑓 − 12
D … (2)
De (1) y (2):
10
𝑓
=
4
𝑓 − 12
⇒ 𝑓 = 20 ⇒ 𝐹 = (−20, 0)
𝐿$: (𝑥 + 12, 𝑦 + 4). (−1, 3)
𝐿$: −𝑥 + 3𝑦 = 0
𝑑(𝐹, 𝐿$) =
|20|
√10
= 2√10
⇒ 𝐻 = 𝐹 + 4√10
(1, −3)
√10
= (−20, 0) + 4(1, −3) = (−16, −12)
⇒ 𝐻𝑄
000000⃗ = 𝑄 − 𝐻 = (−12, −4) − (−16, −12) = (4, 8) ∥ (1, 2)
𝑢
- =
(1, 2)
√5
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝐻𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(&,$)(−4, 12) =
1
2
(−4, 12). (1, 2)
5
(1, 2)
𝑉𝐹
00000⃗ = (2, 4) ⇒ 𝑝 = 2√5, 𝐹 − 𝑉 = (2, 4) ⇒ 𝑉 = (−22, −4)
𝒫 = J(−22, −4) + 𝑥′
(1, 2)
√5
+ 𝑦′
(−2, 1)
√5
𝑦'$
M = 8√5𝑥′O
F X -
Î
1 { (1, )}
L t m
= FT
Î 2 {( 12, 4) (3,1)}
L t
= - - +
( 12, 4)
Q = - -
𝑄 = (−12, −4)
𝑌
𝐹 = (−𝑓, 0)
𝑇
𝑀 = (0, 10)
𝐿&
𝐿$
𝑋
𝑂
𝜃
𝜃
𝐻 𝐿!
𝑉
𝑋′
𝑌′

31. P es una parábola que contiene a los puntos (0, 2), (15, 2) y su eje focal tiene por
ecuación , . La recta ,
contiene al vértice V de P tal que L y determinan un ángulo cuya .
La distancia del punto (15, 2) a la recta directriz de P es , halle la ecuación vectorial
de P.
32. P es una parábola de foco F = (4, 6) , parámetro , eje focal de pendiente
positiva m, es tangente a P en el punto B, tal que N = (15, 3),
, es tangente a P en el punto T tal que
, , , A es un punto medio de tal que, ,
, .Si el punto y , halle la ecuación
vectorial de P.
33. P es una parábola con foco F, directriz , .
es tangente a P en Q tal que y ,
es tangente a P en , . Halle la
34. P es una parábola con vértice ; y foco F tal que
, . El eje X es tangente a P en . En un nuevo sistema , el
eje es tangente a P en B, eje y ,
es el origen del sistema . En el sistema , B , C y T tiene las siguientes
coordenadas , y , . Halle la
ecuación de P en el sistema .
35. P es una parábola que se encuentra en el I cuadrante y se abre hacia a la derecha
y son rectas tangentes a P en los puntos
simétricos con respecto al eje de P, la recta L contiene a los puntos de tangencia, si el
área del triángulo formado por las rectas y mide 96 , halle la ecuación
vectorial de P.
36. EQPM es un rectángulo, sentido horario, donde pertenece a la directriz (con
pendiente negativa) de una parábola P con foco , P Î P , N es un punto en la
mediatriz de , N se encuentra en la región exterior del rectángulo EQPM, relativo a
tal que . Si (8, -6) , M = (20, 0) , t > 0. Halle
la ecuación vectorial de P.
E
L
{(5,2) (1, )}
E
L t m
= + 1
m > {(0,2) (1, )}
L t n
= + 1
n < -
E
L q tan 2
q =
5 5
r E
L
1 1
{N (1, )}
L t m
= +
1
O m m
< < 2 2
{ (1, )}
L T t m
= + 1 2
m m m
< <
2 { }
E
L L M
Ç = 2 1 { }
L L C
Ç = MT AB r
=
(1, )
AB k m
=
!!!
"
0
k > N BC
Î 26
BN =
{ }
(1, )
D
L A t n
= + 1
n < - ( 6,3)
A= -
{ }
1 (5,6) (1, )
L t m
= + 2 m
< (4,1) FQ
Î
{ }
2 (1, 1) (4,7)
L t
= - + ( )
6 , 3
T kn k
= - - + 0
k >
( )
,3
V r r
= - 0
r > ( )
3,1
VF t
=
!!!
"
0
t > ( )
6 65,0
T = ' '
X Y
X +
¢ ' eje
X X C
Ç = ( )
,3
R k k
= - 0 k r
< <
' '
X Y ' '
X Y
( )
' 2 13,0
B = ( )
' 6 13,0
C = ( )
' 14 13,
T e
= 0
e >
' '
X Y
1: 7 13 0
L x y
- + = 2:7 5 0
L x y
- - =
1 2
,
L L L
2
u
EQ
EM
F Î
EF
EM °
= 90
ˆM
N
E EN =
!!!"
(2,11)
FP t
=
!!!
"

37. P es una parábola con foco eje , el eje Y es tangente a P en ,
, , y son puntos de P donde
, V es el vértice de P, halle la ecuación de P.
38. es tangente a una parábola P con foco , eje
focal de pendiente positiva. Si el origen de coordenadas es un punto de P, halle la
39. P es una parábola con vértice V, foco F tal que , es
tangente a P en T = (25, 30); M y N son puntos de la directriz y del eje focal en ese
orden, tal que , // eje focal, es una recta normal a P en B, sí
. Halle la ecuación vectorial de la parábola.
40. P es una parábola de foco F , eje focal de pendiente m. , ,
son rectas tangentes a P en Q y T respectivamente de manera
que . Se ubica el punto H = (- 6, 3) en la recta directriz de P tal que
, C = (2, 4) es un punto en la prolongación de . Halle la ecuación vectorial
de P.
41. Sea P una parábola con foco F = (4, 0), directriz D, eje focal con pendiente positiva.
es una recta tangente a P, si donde .
Halle la ecuación vectorial de P .
Solución
Es igual al problema 6.
42. P es una parábola con foco F, vértice V y directriz D, las rectas
y son tangentes a la parábola en los puntos y
respectivamente. Si (3, -8) , halle la ecuación vectorial de P.
43. P es una parábola con foco F = (0, f ) , eje focal L, recta directriz D,
, el eje es tangente a P. Halle
a) La ecuación vectorial de P
b) Las coordenadas del punto de tangencia con el eje X.
44. P es una parábola con foco F = (-5, -1) y eje con pendiente positiva, LT: y
LN: y = -5 son rectas tangente y normal respectivamente a P en el punto P. Halle la
ecuación vectorial de P si Q = (7, -5) pertenece a la directriz de P.
F Î X + 5
0,
4
T
æ ö
= ç ÷
è ø
1
,4
2
A
æ ö
= ç ÷
è ø
9
,11
2
B
æ ö
= ç ÷
è ø
1
,
2
V k
æ ö
= ç ÷
è ø
9
, 4
2
C
æ ö
= -
ç ÷
è ø
0
k <
11
1, ( 1,8)
2
T
L t
ì ü
æ ö
= - + -
í ý
ç ÷
è ø
î þ
(5, 10)
F -
(1,0) 0
comp VF >
!!!
" 6
1,
7
T
L T t
ì ü
æ ö
= +
í ý
ç ÷
è ø
î þ
6
0
7
E
m
< < MT
!!!"
MN
136
MB BN
= =
!!!" !!!"
{ }
1 1
(5,6) (1, )
L t m
= + t Î!
( )
{ }
2 (5,6) 4,7
L t t
= + Î!
1
7
0
4
m m
< < < D
L
D
TH L
^ FQ
:3 4 37 0
T
L x y
- - = //( 2,11)
QF -
!!!"
T
Q L D
Î Ç
1 :4 3 29 0
L x y
- + =
2 :6 8 19 0
L x y
+ - = 1 (4,15)
P = 2
P
D
Î
0
f <
( 6, 8)
L D
Ç = - - X +
1
-
=
x

45. P es una parábola donde los ejes e son tangentes a la P en P1 y P2 = (0, 24)
respectivamente. El eje focal interseca a en R, por R se traza una recta L paralela
a que corta al eje en . Halle la ecuación vectorial de P .
Solución
De la figura:
5𝑘 = 24 ⇒ 𝑘 =
24
5
⟹ 𝐻 = B0,
12
5
D ⟹ 𝐹 = B−𝑓,
12
5
D ⇒ 𝐹𝑂
00000⃗ = 𝑂 − 𝐹 = B𝑓, −
12
5
D
Además:
𝐹𝑃$
0000000⃗ = 𝑃$ − 𝐹 = (0,24) − B−𝑓,
12
5
D = B𝑓,
108
5
D
Como:
𝐹𝑂
00000⃗. 𝐹𝑃$
0000000⃗ = 0 ⇒ 𝑓$
= B
12
5
D B
108
5
D ⇒ 𝑓 =
36
5
⇒ 𝐹 = B−
36
5
,
12
5
D
Por otra parte, tenemos:
𝐴 = B0, −
96
5
D ⇒ 𝐴𝐹
00000⃗ = 𝐹 − 𝐴 = B−
36
5
,
12
5
D − B0, −
96
5
D = B−
36
5
,
108
5
D ∥ (−1, 3)
⇒ 𝑢
- =
(−1, 3)
√10
𝑉𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(
)𝑂𝐹
00000⃗ =
1
2
𝑝𝑟𝑜𝑦(6&,%) B−
36
5
,
12
5
D =
1
2
E−
36
5 ,
12
5 F . (−1, 3)
10
(−1, 3)
-
X +
Y
-
X
2
1P
P +
Y ÷
ø
ö
ç
è
æ
5
96
,
0
𝑉
𝑅
𝑃&
X
Y
L
X’
𝐹
𝐻
𝑄 = B0,
96
5
D
𝐿!
𝛼
𝛼
𝜃
𝜃
𝜃
4𝑘
4𝑘
𝑘
𝑘
2
𝛼
𝐴
𝑂
𝑢
-
𝑃$ = (0,24)

𝑉𝐹
00000⃗ =
18
25
(−1, 3) ⇒ 𝑉 = B−
162
25
,
6
25
D , 𝑝 =
18
25
√10
Luego la ecuación de la Parábola es:
𝒫 = JB−
162
25
,
6
25
D + 𝑥′
(−1, 3)
√10
+ 𝑦′
(−3, −1)
√10
∕ 𝑦′$
= 4 B
18
25
√10D 𝑥′O

CB-101_Ejercicios_semana_11_FB101W.pdf

Recomendados

Recomendados

Más contenido relacionado

La actualidad más candente

La actualidad más candente (20)

Similar a CB-101_Ejercicios_semana_11_FB101W.pdf

Similar a CB-101_Ejercicios_semana_11_FB101W.pdf (20)

Último

Último (20)

CB-101_Ejercicios_semana_11_FB101W.pdf