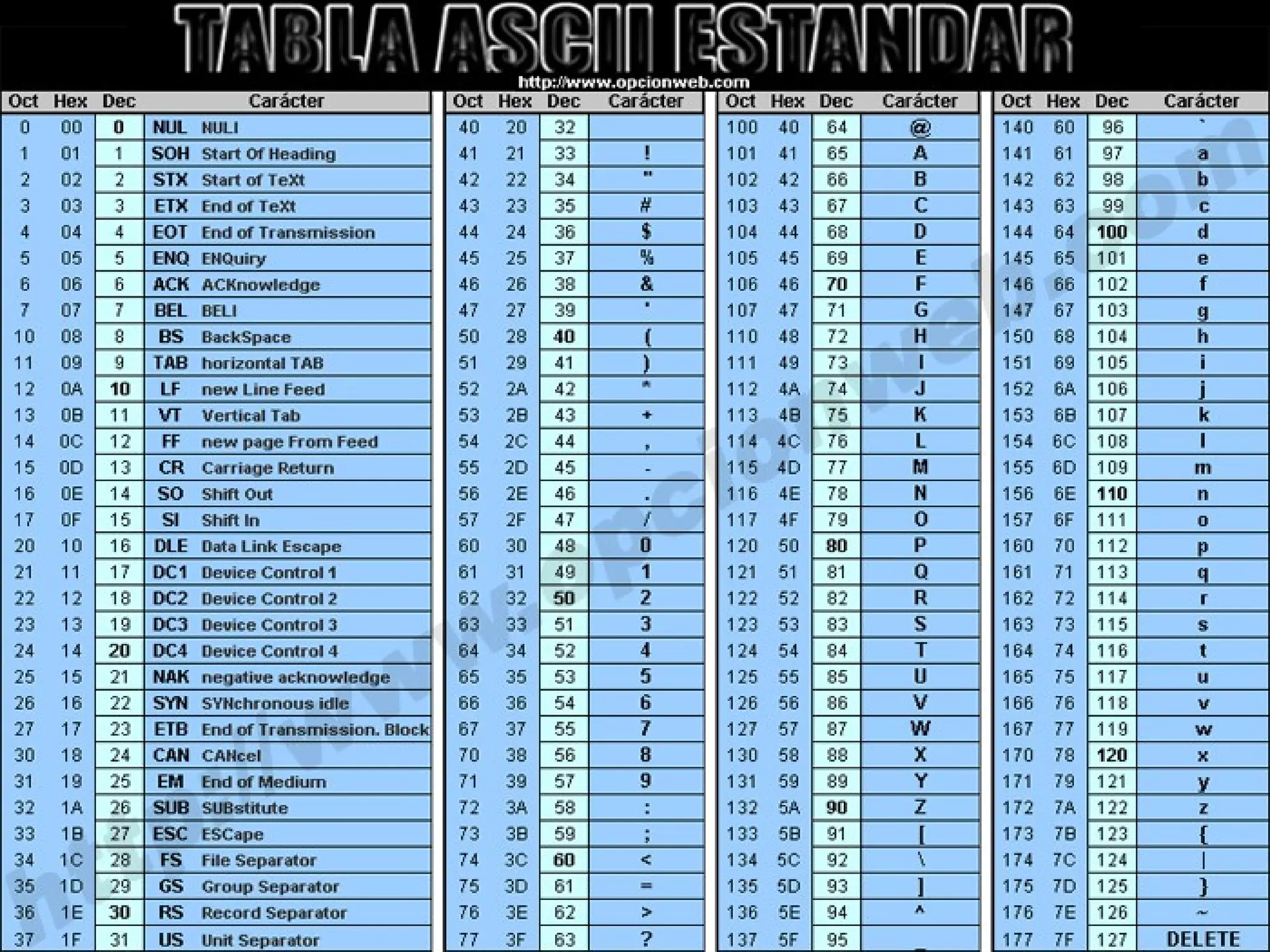
Este documento trata sobre los sistemas numéricos y la representación de datos en la computadora. Explica los componentes de los sistemas numéricos como la base y el alfabeto, e introduce los sistemas binario, octal, decimal y hexadecimal. También presenta el teorema fundamental de numeración para realizar conversiones entre sistemas. Finalmente, cubre brevemente la representación de datos numéricos, de texto, imágenes y sonido en la computadora.

1. Introducción a la Computación
Programa: Análisis de Sistemas
Prof: Erys Piñero
Vladimir Camacaro
Lapso: 2014_1
Profesores: Camacaro Vladimir y Piñero Erys 1

2. Sistemas Numéricos
Definición: Conjunto de símbolos utilizados para la
representación de cantidades, así como las reglas que
rigen dicha representación.
Componentes:
 La base : Indica el numero de símbolos que utiliza el
sistema.
 El alfabeto: Constituyen los símbolos del sistema. Sus
valores varían desde cero hasta la Base-1
Profesores: Camacaro Vladimir y Piñero Erys 2

3.  Sistema binario:
Base = 2
Alfabeto = 0, 1
 Sistema Octal:
Base = 8
Alfabeto = 0, 1, 2, 3, 4, 5, 6, 7
 Sistema Decimal :
Base = 10
Alfabeto = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
 Sistema Hexadecimal:
Base = 16
Alfabeto = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
10 11 12 13 14 15
Profesores: Camacaro Vladimir y Piñero Erys 3

4. TEOREMA FUNDAMENTAL DE NUMERACION
Relaciona una cantidad expresada en cualquier sistema
de numeración con la misma cantidad expresada en el
sistema decimal.
n
No = Σ (dígito) i x (base) i
i=-d
donde: base → valor de la base
i → posición del digito respecto a la coma decimal
d →número de dígitos a la derecha de la coma
n → numero de dígitos a la izquierda de la coma-1
dígito → cada uno de los dígitos que componen el numero.
Profesores: Camacaro Vladimir y Piñero Erys 4

5. Ejemplos
n
No = Σ (dígito) i x (base) i
i=-d
1992 = 2x100+9x101+9x102+1x103
= 2+90+900+1000
3,123 = 3x10-3+2x10-2+1x10-1+3x100
= 0.003 + 0.02 + 0.1 + 3
Profesores: Camacaro Vladimir y Piñero Erys 5

6. Conversiones entre sistemas.
Binario a Decimal: En este caso hay que aplicar
el Teorema Fundamental de la Numeración.
Profesores: Camacaro Vladimir y Piñero Erys 6

7. Ejemplo
Realizar la siguiente conversión : (110.0101)2 = (?)10
Aplicando el teorema se tiene:
2
No = Σ (dígito) i x (2) i = 1x2-4+ 0x2-3+ 1x2-2+ 0x2-1+ 0x20+ 1x21+ 1x22
i=-4
= 0.0625 + 0 + 0.25 + 0 + 0 + 2 + 4
= 6.3125
Resultado (110.0101)2 = (6.3125)10
Profesores: Camacaro Vladimir y Piñero Erys 7

8. En las conversiones de Octal a Decimal y de
Hexadecimal a Decimal también se aplica el Teorema
Fundamental de Numeración.
Profesores: Camacaro Vladimir y Piñero Erys 8

9. Convertir de Decimal a Binario.
Ejemplo:
(19.84)10 = ( ? )2
Parte entera Parte Fraccionaria
Resto Acarreo
19 l 2 0.84x2 = 1.68 1
9 l 2 1 0.68x2 = 1.36 1
4 l 2 1 0.36x2 = 0.72 0
2 l 2 0 0.72x2 = 1.44 1
1 l 2 0 0.44x2 = 0.88 0
0 1
Resultado (19.84)10 = ( 10011.11010… )2
Prueba: 1x24+0x23+0x22+1x21+1x20 + 1x2-1+1x2-2+0x2-3+1x2-4+1x2-5
= 16 + 0 + 0 + 2 + 1 + 0.5 + 0.25 + 0 + 0.0625 + 0.03125 = 19.84
Profesores: Camacaro Vladimir y Piñero Erys 9

10. Convertir de Decimal a Hexadecimal.
Ejemplo:
(570.27)10 = ( ? )16
Parte entera Parte Fraccionaria
Resto Acarreo
570 l 16 0.27x16 = 4.32 4
35 l 16 10 0.32x16 = 5.12 5
2 l 16 3 0.12x16 = 1.92 1
0 2 0.92x16 = 14.72 14
0.72x16 = 11.52 11
Resultado (570.27)10 = ( 23A.451EB… )16
Prueba: 2x162+3x161+Ax160 + 4x16-1+5x16-2+1x16-3+Ex16-4+Bx16-5
= 570 + 48 + 10 + 0.25 + 0.019 + 0.00024 + 0.00021 + 0.0000104
= 570.27

Profesores: Camacaro Vladimir y Piñero Erys 10

11. Convertir de Binario a Hexadecimal y
viceversa
Digito Hexadecimal Digito Binario Ejemplo 1
0 0000 (1111010.11011)2 = (?)16
1 0001
2 0010 0111 1010 . 1101 1000
3 0011 7 A D 8
4 0100 Resultado:
5 0101 (1111010.11011)2 = (7A. D8)16
6 0110
7 0111
8 1000 Ejemplo 2
9 1001
A 1010 (CA.FE)16 = (?)2
B 1011
C 1100 C A . F E
D 1101 1100 1010 . 1111 1110
E 1110 Resultado
F 1111 (CA.FE)16 = (11001010.11111110)2
Profesores: Camacaro Vladimir y Piñero Erys 11

12. Representación de los datos en la
computadora
Datos numéricos : enteros y reales
Textos: ASCII, EBCDIC
Imágenes: Existen 2 métodos básicos
a.- Mapas de bits (píxel)
b.- Mapas de vectores ( descomponer la imagen como una colección
de objetos tales como líneas, polígonos y textos )
Sonidos
Profesores: Camacaro Vladimir y Piñero Erys 12

13. Introducción a la Computación
El Juego de Caracteres
La Tabla ASCII
Profesores: Camacaro Vladimir y Piñero Erys 13