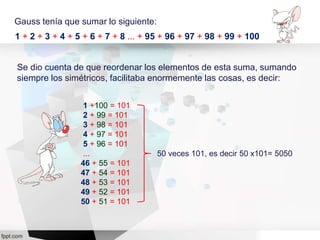
Este documento introduce las sumatorias y resume sus propiedades y ejemplos notables. Explica cómo Gauss resolvió el problema de sumar los números del 1 al 100 de forma ingeniosa al reordenar los términos de manera simétrica. Luego presenta definiciones, propiedades y ejemplos resueltos de sumatorias.

1. SUMATORIAS

2. CONTENIDO
 Introducción
 Definición
 Propiedades
 Sumatorias Notables
 Ejercicios Resueltos
Conclusiones

3. INTRODUCCIÓN
Érase una vez un niño alemán llamado Carl F.
Gauss. Cuando tenía diez años, su profesor de la
escuela, enfadado porque sus alumnos se portaban
mal, le puso un problema matemático al pequeño
Carl y a sus compañeros.
Los niños debían sumar todos los números del
1 al 100, es decir: 1+2+3+4+5+…+98+99+100

4. El profesor se sentó en su silla a leer el periódico,
confiaba en que tendría horas hasta que los niños
sumaran todos los números. Sin embargo, el
pequeño Gauss no tardó ni cinco minutos en ir
hacia el profesor y darle el resultado: 5050.
¿Cómo lo había hecho?

5. Gauss tenía que sumar lo siguiente:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 ... + 95 + 96 + 97 + 98 + 99 + 100
Se dio cuenta de que reordenar los elementos de esta suma, sumando
siempre los simétricos, facilitaba enormemente las cosas, es decir:
1 +100 = 101
2 + 99 = 101
3 + 98 = 101
4 + 97 = 101
5 + 96 = 101
...
46 + 55 = 101
47 + 54 = 101
48 + 53 = 101
49 + 52 = 101
50 + 51 = 101
50 veces 101, es decir 50 x101= 5050

6. De donde se deduce la fórmula de la sumatoria de los n primeros números.
𝑖=1
𝑛
𝑖 = 1 + 2 + 3 + 4 + ⋯ + 𝑛 =
𝑛 𝑛 + 1
2
Conociendo esta fórmula podremos resolver el problema planteado a
Gauss, que fue de sumar los 100 primero números.
𝑖=1
100
𝑖 = 1 + 2 + 3 + 4 + ⋯ + 100 =
100 100 + 1
2
𝑖=1
100
𝑖 = 1 + 2 + 3 + 4 + ⋯ + 100 = 50(101)
𝑖=1
100
𝑖 = 1 + 2 + 3 + 4 + ⋯ + 100 = 5050

7. DEFINICIÓN
La sumatoria es la operación de la adición de una secuencia de
números, el resultado es la suma total.
NOTACIÓN
𝒕 𝟏 + 𝒕 𝟐 + 𝒕 𝟑+…+𝒕 𝒏=
𝑖=𝑎
𝑛
𝑡𝑖
Índice superior
Término general
Índice inferior
sigma

8. P1. El número de sumandos y de términos de una sumatoria
es igual al índice superior menos el índice inferior mas la
unidad.
𝑖=𝑎
𝑛
𝑡𝑖= 𝒏−𝒂 +𝟏=𝒏ú𝒎𝒆𝒓𝒐 𝒅𝒆 𝒕é𝒓𝒎𝒊𝒏𝒐𝒔
Ejemplo:
Hallar el número de términos de la siguiente expresión:
𝑖=5
45
𝑖= 45−5 +1=41 𝑡é𝑟𝑚𝑖𝑛𝑜𝑠
PROPIEDADES

9. P2. La sumatoria de una constante es igual al producto del número
de sumandos por la constante.
𝑖=𝑎
𝑛
𝑘 = [ 𝑛 − 𝑎 + 1]. 𝑘
Ejemplo:
Hallar la sumatoria de la siguiente expresión:
𝑖=5
45
4 = 45 − 5 + 1 . 4 = 164
PROPIEDADES

10. P3. La sumatoria en el que el término general es una suma algebraica
ésta se puede descomponer en sumatorias independientes.
𝑖=𝑎
𝑛
(𝑘𝑖2
+ 𝑘´
𝑖) =
𝑖=𝑎
𝑛
𝑘𝑖2
+
𝑖=𝑎
𝑛
𝑘´
𝑖
Ejemplo:
𝑖=𝑎
𝑛
(2𝑖2 + 3𝑖) =
𝑖=𝑎
𝑛
2𝑖2 +
𝑖=𝑎
𝑛
3𝑖
Donde: k y k´ son constantes.
PROPIEDADES

11. P4. Una sumatoria cuyo índice inferior no es la unidad puede
descomponerse de ésta manera:
𝑖=𝑎
𝑛
𝑡𝑖 =
𝑖=1
𝑛
𝑡𝑖 −
𝑖=1
𝑎−1
𝑡𝑖
Ejemplo:
Hallar la sumatoria de la siguiente expresión:
𝑖=5
11
𝑖 =
𝑖=1
11
𝑖 −
𝑖=1
4
𝑖
Donde: a ≠ 𝟏
PROPIEDADES

12.  SUMATORIAS
NOTABLES

13. 𝑖=1
𝑛
𝑖 = 1 + 2 + 3 + 4 + ⋯ + 𝑛 =
𝑛 𝑛 + 1
2
 Los “n” primeros números naturales
SUMATORIAS NOTABLES

14.  Los “n” primeros números pares naturales
𝑖=1
𝑛
2𝑖 = 2+ 4 + 6 + 8 + ⋯ + 𝟐𝒏 = 𝑛 𝑛 + 1
Demostración:
𝑖=1
𝑛
2𝑖 = 2+ 4 + 6 + 8 + ⋯ + 𝟐𝒏
𝑖=1
𝑛
2𝑖 = 2(1+ 2 + 3 + 4 + ⋯ + 𝒏)
𝑖=1
𝑛
2𝑖 = 2 [
n(n+1)
2
]
𝑖=1
𝑛
2𝑖 = 𝑛 𝑛 + 1 lqqd
SN primeros N
Factorización
SUMATORIAS NOTABLES

15. 𝑖=1
𝑛
(2𝑖 − 1) = 1 + 3 + 5 + 7 + ⋯ + (2𝑛 − 1) = 𝑛2
 Los “n” primeros números impares naturales.
Demostración:
𝑖=1
𝑛
2𝑖 − 1 =
𝑖=1
𝑛
2𝑖 −
𝑖=1
𝑛
1 P3:
𝑖=1
𝑛
2𝑖 − 1 = [𝑛 𝑛 + 1 − 𝑛 − 1 + 1 1] SN #pares y P2:
𝑖=1
𝑛
2𝑖 − 1 = [𝑛 𝑛 + 1 − 𝑛 − 1 + 1 1]
𝑖=1
𝑛
2𝑖 − 1 = 𝑛2 + 𝑛 − 𝑛 =
simplificación
𝑖=1
𝑛
2𝑖 − 1 = 𝑛2 lqqd
SUMATORIAS NOTABLES

16.  Los “n” primeros números cuadrados perfectos
𝑖=1
𝑛
𝑖2 = 12 + 22 + 32 +
42 + ⋯ + 𝑛2 =
𝑛 𝑛 + 1 (2𝑛 + 1)
6
SUMATORIAS NOTABLES

17.  Los “n” primeros números cubos perfectos.
𝑖=1
𝑛
𝑖3
= 13
+23
+33
+43
+ ⋯ + 𝑛3
= [
𝑛 𝑛 + 1
2
]2
SUMATORIAS NOTABLES

18.  Los “n” primeros números cuartos perfectos.
𝑖=1
𝑛
𝑖4
= 14
+24
+34
+44
+ ⋯ + 𝑛4
=
𝑛 𝑛 + 1 (2𝑛 + 1)(3𝑛2
+ 3𝑛 − 1)
30
SUMATORIAS NOTABLES

19.  Los “n” primeras potencias.
𝑖=1
𝑛
𝑎 𝑖 = 𝑎1+𝑎2+𝑎3+𝑎4+ ⋯ + 𝑎 𝑛 =
𝑎 𝑛+1 − 𝑎
𝑎 − 1
SUMATORIAS NOTABLES

20. EJERCICIOS
RESUELTOS

21. 1. Escriba con notación ∑
a) 3+9+27+81+…(10 términos)
Resolución: 3+9+27+81+…(10 términos)
𝑖=1
10
3𝑖
𝒕 𝟏 =3
𝒕 𝟐 =9 =𝟑 𝟐
𝒕 𝟑 =27=𝟑 𝟑
𝒕 𝟒 =81=𝟑 𝟒
3+9+27+81+…(10 términos) =
…
EJERCICIOS RESUELTOS

22. b) 2+6+10+14+18…(10 términos)
Resolución: 2+6+10+14+18…(10 términos)
𝒕 𝟏 =2
𝒕 𝟐 = 6 = 2(3)
𝒕 𝟑 = 10 = 2(5)
𝒕 𝟒 = 14 = 2(7)
…
2+6+10+14+18…(10 términos) =
𝑖=1
10
2(2𝑛 − 1)
EJERCICIOS RESUELTOS

23. 2. Hallar
𝑥=1
30
(3𝑥 + 2)
Resolución:
:propiedad 3
𝑥=1
30
3𝑥 + 2 =
𝑥=1
30
3𝑥 +
𝑥=1
30
2
𝑥=1
30
3𝑥 + 2 = 3
𝑥=1
30
𝑥 +
𝑥=1
30
2
𝑥=1
30
3𝑥 + 2 = 3(
30 30 + 1
2
) + [ 30 − 1 + 1]. 2
𝑥=1
30
3𝑥 + 2 = 3(465) + 60
𝑥=1
30
3𝑥 + 2 = 1455
:S.N y :propiedad 2
:propiedad 2

24. 3. Calcular P , si P = 3 +24 + 81 + 192 +… + 8232
Resolución:
:factorizando
𝑃 = 3 + 24 + 81 + 192 + … + 8232
𝑃 = 3
𝑥=1
14
𝑥3
:S.N. cubos
𝑃 = 3(1 + 8 + 27 + 64 + … + 2744)
𝑃 = 3(13 + 23 + 33 + 43 + … + 143)
𝑃 = 3
14(14+1)
2
2
𝑃 = 3 7(15) 2
𝑃 =33075

25. 4. Hallar n:
Resolución:
:S.N. números pares
:Ec. De 2 grado
𝑛(𝑛 + 1) = 342
𝑥=1
𝑛
2𝑥 = 342
𝑥=1
𝑛
2𝑥 = 342
𝑛2 + 𝑛 − 342 = 0
(n-18)(n+19)= 0
n-18= 0
n= 18

26. 5. Hallar S: Si S = 4 + 7 +12 + 19 + . ..
Resolución:
:Propiedad 3
15 términos
S = 4 + 7 +12 + 19 + . ..
15 términos
𝑆 =
𝑖=1
15
(𝑛2
+3)
𝑆 =
𝑖=1
15
𝑛2
+
𝑖=1
15
3 :S.N. y Propiedad 2
𝑆 =
15(15+1)(2(15)+1)
6
+(15-1+1)3
𝑆 = 1240+45
𝑆 = 1285

27. 6. Calcular E:
Resolución:
:Decimal a fracción
:Factorizando
E= 100
𝐸 = 0,01 + 0,03 + 0,05 + … + 19,99
𝐸 = 0,01 + 0,03 + 0,05 + … + 19,99
𝐸 =
1
100
+
3
100
+
5
100
+ ⋯ +
1999
100
𝐸=
1
10
1 + 3 + 5 + ⋯ + 1999 2n-1= 1999
2n = 2000
n = 1000𝐸=
1
10
10002

28. 7. Se tiene:
Resolución:
A:Encontremos el valor de 𝑅𝑀
𝑴𝑨𝑹=1+2+3+…+ 43
Encontrar el valor de: 1 +2 +3 +…+ 𝑹𝑴
𝑀𝐴𝑅=1+2+3+…+ 43
𝑀𝐴𝑅=
43(43+1)
2
𝑀𝐴𝑅=946
Por Tanto:
M =9
A=4
R=6
B: Hallando 1 +2 +3 +…+ 𝑹𝑴
1 +2 +3 +…+ 𝟔𝟗
2n-1=69
n=35
Aplicando S.N Números impares
1 +2 +3 +…+ 𝟔𝟗 = 352
1 +2 +3 +…+ 𝟔𝟗 = 𝟏𝟐𝟐𝟓

29. 8. Un ómnibus salió de su paradero inicial con 7
pasajeros, y en cada estación suben 2 pasajeros
más de lo que subieron en la estación anterior.
Si al llegar a su paradero final se contaron con 520
pasajeros. ¿En cuántas estaciones se detuvo el
ómnibus a recoger pasajeros?
Resolución:
Inicio: 1° 2° 3° … n° Final
7 9 11 13 __ 520
Total de pasajeros: 7 +9+11+13+…+n=520
𝑛2
+ 62
= 520
𝑖=7
𝑛
2𝑛 − 1 = 520
𝑖=1
𝑛
2𝑛 − 1 −
𝑖=1
6
2𝑛 − 1 = 520
𝑛= 22
𝑷𝒆𝒓𝒐 𝒊𝒏𝒊𝒄𝒊𝒂𝒍𝒎𝒆𝒏𝒕𝒆 𝒚𝒂 𝒕𝒆𝒏𝒊𝒂 𝟕 𝒑𝒂𝒔𝒂𝒋𝒆𝒓𝒐𝒔, 𝒆𝒍 𝒐𝒎𝒏𝒊𝒃𝒖𝒔 𝒑𝒂𝒓𝒐 𝒆𝒏 𝟐𝟏 𝒆𝒔𝒕𝒂𝒄𝒊𝒐𝒏𝒆𝒔

30. 9. Un obrero ha ahorrado este mes S/. 178 soles y tiene con esto S/. 1410
en la caja de ahorros, habiendo economizado cada mes S/ 12
más que el mes anterior.¿ Cuánto ahorro el primer mes?
Resolución:
1° 2° 3° … n°
Mes Mes Mes 1° Mes
actual pasado antepasado de ahorro
178 + 166 + 154 + … +(190-12n) = 1410
190𝑛 − 12
𝑛(𝑛+1)
2
= 520
𝑖=1
𝑛
190 − 12
𝑖=1
𝑛
𝑖 = 1410
𝑛= 15
𝑬𝒍 𝟏° 𝒎𝒆𝒔 𝒂𝒉𝒐𝒓𝒓𝒐: 𝟏𝟗𝟎 − 𝟏𝟐 𝟏𝟓 = 𝟏𝟎
𝑖=1
𝑛
190 − 12𝑖 = 1410 190𝑛 −6𝑛2
− 6𝑛 = 520
6𝑛2 − 184 – 520 = 0
3𝑛2
− 92 - 260 = 0
(3n+8)(n-15) = 0

31. 10. Se contrata a un obrero para cavar en busca de fósiles
prometiéndole pagar una suma por el primer fósil que
encuentre y que luego se le irá duplicando dicha suma para
Cada nuevo fósil encontrado. Si encuentra 12 fósiles y recibe
S/. 12285 ¿Cuánto le pagaron por el octavo fósil encontrado?
Resolución:
1° 2° 3° 4° 5° 6° 7° 8° …. 12°
Fósil Fósil Fósil Fósil Fósil Fósil Fósil Fósil Fósil
x + 2x + 4x + 8x + 16x + 32 x + 64 x + 128x +…+ = 12285
x( 20
+ 21
+ 22
+ 23
+ 24
+ 25
+ 26
+ 27
+ 28
+ 29
+ 210
+ 211
) = 12285
x+𝑥[
212−2
2−1
]= 12285
Por 𝐞𝐥 𝟖° 𝒇ó𝒔𝒊𝒍 𝒆𝒏𝒄𝒐𝒕𝒓𝒂𝒅𝒐 𝒍𝒆 𝒑𝒂𝒈𝒂𝒓𝒐𝒏: 𝟏𝟐𝟖 𝟑 = 𝟑𝟖𝟒
𝑥 + 𝑥
𝑖=1
11
2𝑖 = 12285
4095𝑥 = 12285
𝑥 = 3

32.  Las sumatorias notables, son sumatorias ya calculadas
que nos permiten resolver problemas.
 La definición de sumatoria ayuda en el entendimiento
base en problemas de sumatorias.
 Las propiedades de las sumatorias
facilitan en la resolución de problemas.
CONCLUSIONES