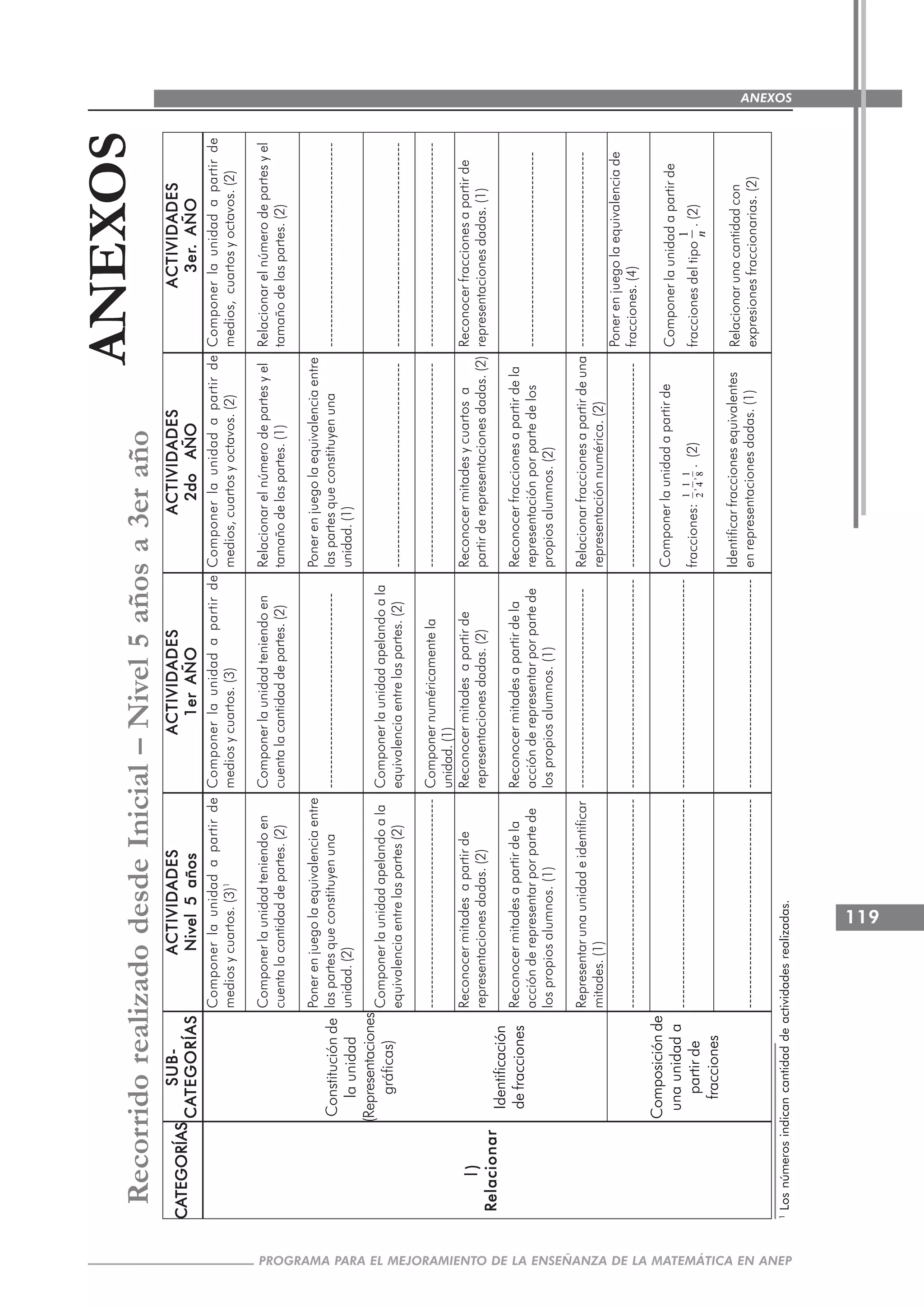
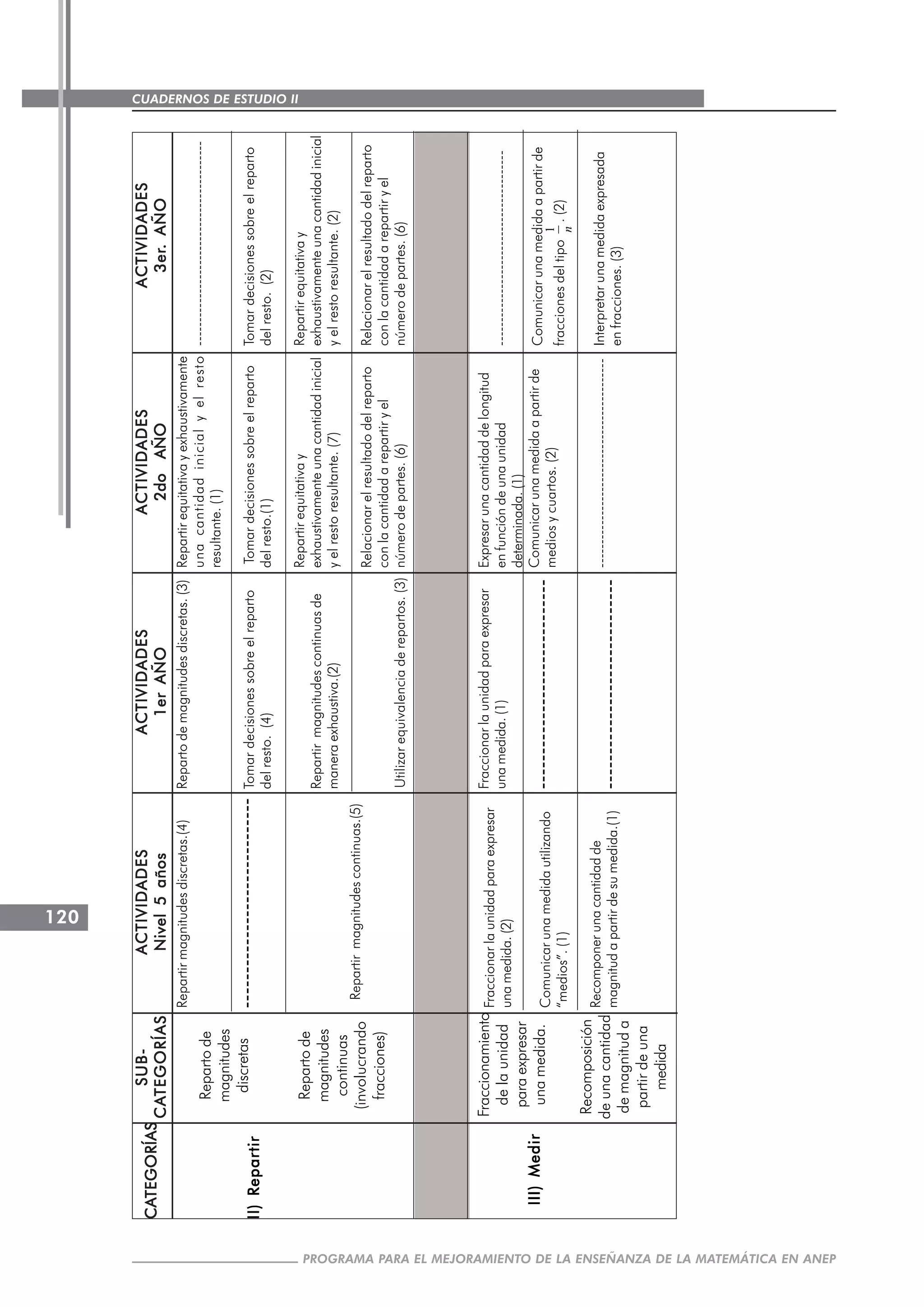
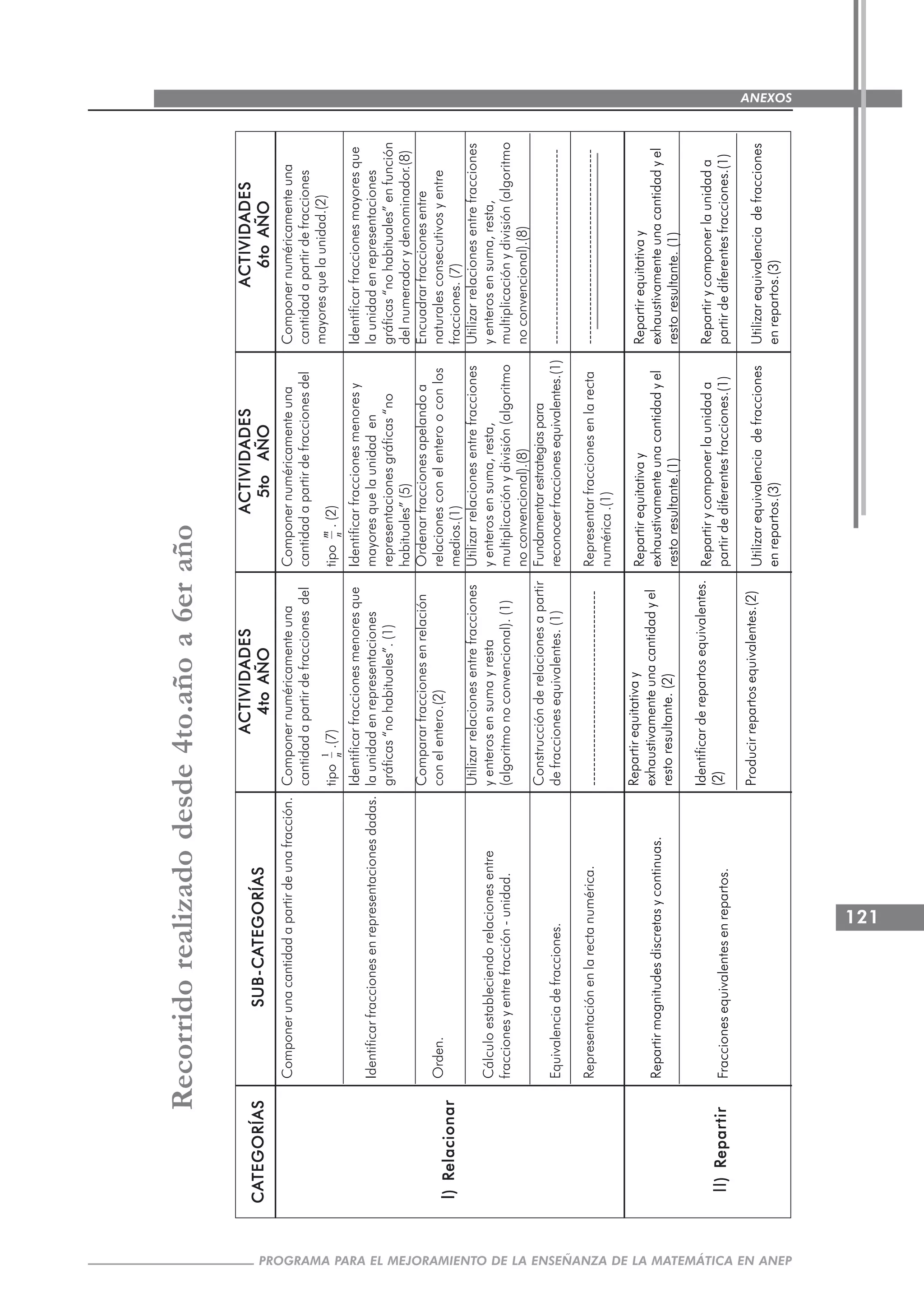
Este documento describe un proyecto realizado en 2005 para estudiar la enseñanza de fracciones en la escuela primaria uruguaya. El proyecto involucró a maestros de dos escuelas de práctica en Montevideo y tuvo como objetivos introducir innovaciones en la enseñanza de matemáticas, profundizar los conocimientos matemáticos de los maestros y proporcionar herramientas para analizar procesos de aprendizaje.