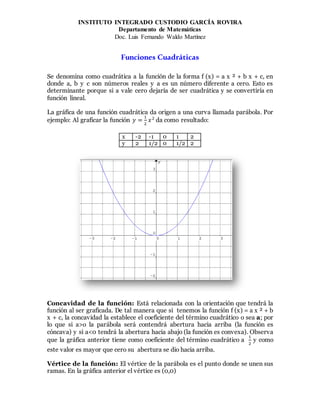
1.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
Funciones Cuadráticas
Se denomina como cuadrática a la función de la forma f (x) = a x ² + b x + c, en
donde a, b y c son números reales y a es un número diferente a cero. Esto es
determinante porque si a vale cero dejaría de ser cuadrática y se convertiría en
función lineal.
La gráfica de una función cuadrática da origen a una curva llamada parábola. Por
ejemplo: Al graficar la función 𝑦 =
1
2
𝑥2
da como resultado:
x -2 -1 0 1 2
y 2 1/2 0 1/2 2
Concavidad de la función: Está relacionada con la orientación que tendrá la
función al ser graficada. De tal manera que si tenemos la función f (x) = a x ² + b
x + c, la concavidad la establece el coeficiente del término cuadrático o sea a; por
lo que si a>o la parábola será contendrá abertura hacia arriba (la función es
cóncava) y si a<0 tendrá la abertura hacia abajo (la función es convexa). Observa
que la gráfica anterior tiene como coeficiente del término cuadrático a
1
2
y como
este valor es mayor que cero su abertura se dio hacia arriba.
Vértice de la función: El vértice de la parábola es el punto donde se unen sus
ramas. En la gráfica anterior el vértice es (0,0)

2.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
Tienen dos
raíces
Tienen una
raíz
No posee
raíces reales
Raíces de la función: Las raíces o ceros como también se le conocen son
aquellos valores de x para los cuales la expresión vale 0, es decir los valores de x
tales que y = 0. Gráficamente corresponden a las abscisas de los puntos donde la
parábola corta al eje x, como lo podemos ver a continuación:
Una función cuadrática se convierte en una ecuación cuadrática al igualar sus
términos a cero.
Función Cuadrática: f (x) = a x ² + b x + c
Ecuación Cuadrática: a x ² + b x + c = 0
Elementos de una ecuación cuadrática: Una ecuación cuadrática se dice que está
completa cuando posee los siguientes elementos:
a x ² + b x + c = 0
Solución de una ecuación cuadrática: De acuerdo a los elementos que posee la
ecuación, se puede utilizar uno o varios procedimientos para determinar sus raíces.
 Si posee el término cuadrático y el término independiente, se resuelve despejando y
extrayendo la raíz cuadrada. Veamos:
Resolver la ecuación: 2x2 – 18 = 0
Solución: 2x2 = 18 ‘transponiendo término
x2 = 9 ‘dividiendo entre 2
x = 3 ‘extrayendo raíz cuadrada
De esta manera las raíces son 3 y -3
TérminoCuadrático
Términolineal
Términoindependiente

3.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
Resolver la ecuación: x2 – 121 = 0
Solución: x2 = 121 ‘transponiendo término
x = 11 ‘extrayendo raíz cuadrada
Rta. Las raíces son 11 y -11
 Si posee el término cuadrático y el término lineal, se resuelve por factorización
(factor común). Veamos:
Resolver la ecuación x2 – 5x = 0
Solución: x(x – 5) = 0 ‘factorizando
x = 0 ‘igualando primer factor
x1 = 0 ‘primera raíz
x – 5 = 0 ‘igualando segundo factor
x = 0 + 5 ‘despejando
x2 = 5 ‘segunda raíz
Rta. Las raíces son 0 y 5
Resolver la ecuación 3x2 + 6x = 0
Solución: 3x(x + 2) = 0 ‘factorizando
3x = 0 ‘igualando primer factor
x = 0/3 ‘despejando
x1 = 0 ‘primera raíz
x + 2 = 0 ‘igualando segundo factor
x = 0 – 2 ‘despejando
x2 = -2 ‘segunda raíz
Rta. Las raíces son 0 y -2
 Si la ecuación posee todos sus elementos, se puede resolver por factorización o por
fórmula general. Veamos:
Resolver la ecuación x2 + 8x + 15 = 0
Solución Por factorización:
(x + 3) (x + 5) = 0
x + 3 = 0
x = -3
x + 5 = 0
x = -5
Rta: Las raíces son -3 y -5

4.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
Solución por fórmula general:
La fórmula general para resolver ecuaciones cuadráticas es 𝒙 =
−𝒃±√𝒃𝟐−𝟒𝒂𝒄
𝟐𝒂
. Por
otro lado recuerda que en la ecuación x2 + 8x + 15 = 0; a = 1, b = 8 y c = 15, de esta
manera remplazando obtenemos:
𝒙 =
−𝟖 ± √(𝟖)𝟐 − 𝟒(𝟏)(𝟏𝟓)
𝟐(𝟏)
𝒙 =
−𝟖 ± √𝟔𝟒 − 𝟔𝟎
𝟐
𝒙 =
−𝟖 ± √𝟒
𝟐
𝒙 =
−𝟖 ± 𝟐
𝟐
𝒙𝟏 =
−𝟖 + 𝟐
𝟐
=
−𝟔
𝟐
= −𝟑
𝒙𝟐 =
−𝟖 − 𝟐
𝟐
=
−𝟏𝟎
𝟐
= −𝟓
Como verás ambos métodos arrojan las mismas respuestas.
Ejemplo 2: Resolver la ecuación 6x2 – 19x – 7 = 0
Solución Por factorización:
(6x)2 – 19(6x) – 7(6) = 0
(6x)2 – 19(6x) – 42 = 0
(6x – 21) (6x + 2) = 0
(2x – 7)(3x + 1) = 0
2x – 7 = 0
2x = 7
x =
𝟕
𝟐
3x + 1 = 0
3x = -1
x = −
𝟏
𝟑
Rta: Las raíces son
𝟕
𝟐
y −
𝟏
𝟑
Solución por fórmula general:
En la ecuación 6x2 – 19x – 7 = 0; a = 6, b = -19 y c = -7, de esta manera remplazando
obtenemos:

5.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
𝒙 =
−(−𝟏𝟗)± √(−𝟏𝟗)𝟐 − 𝟒(𝟔)(−𝟕)
𝟐(𝟔)
𝒙 =
𝟏𝟗 ± √𝟑𝟔𝟏 + 𝟏𝟔𝟖
𝟏𝟐
𝒙 =
𝟏𝟗 ± √𝟓𝟐𝟗
𝟏𝟐
𝒙 =
𝟏𝟗 ± 𝟐𝟑
𝟏𝟐
𝒙𝟏 =
𝟏𝟗 + 𝟐𝟑
𝟏𝟐
=
𝟒𝟐
𝟏𝟐
=
𝟕
𝟐
𝒙𝟐 =
𝟏𝟗 − 𝟐𝟑
𝟏𝟐
=
−𝟒
𝟏𝟐
= −
𝟏
𝟑
Nuevamente las mismas respuestas.
Discriminante y raíces: Se llama discriminante a la expresión b2 – 4ac. Ésta nos indica
la naturaleza de las raíces que deseamos encontrar. Siendo a, b y c números reales, con
a0, se tiene que:
b2 – 4ac > 0 hay dos raíces reales
b2 – 4ac = 0 hay una sola raíz real
b2 – 4ac < 0 hay dos raíces imaginarias
Por ejemplo en la última ecuación resuelta, 6x2 – 19x – 7 = 0 teníamos los valores a = 6,
b = -19 y c = -7, al verificar la naturaleza de la discriminante obtenemos:
(−𝟏𝟗)𝟐
− 𝟒(𝟔)(−𝟕) = 361 + 168 = 529
Ahora como 529>0 obtuvimos dos respuestas reales:
𝟕
𝟐
y −
𝟏
𝟑
LABORATORIO
1. Con la ayuda de una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y saca las conclusiones:
a. y = 3x2
b. y = x2
c. y = 5x2
d. y = 1/2x2
2. Utiliza una calculadora graficadora o una computadora con software graficador y
representa las siguientes funciones. Saca tus conclusiones:
a. y = -2x2 – 1
b. y = -x2
c. y = -4x2

6.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
3. Apoyándote en una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y saca las conclusiones:
a. y = 2x2 + 3
b. y = -3x2 + 1
c. y = -6x2 – 1
d. y = -1/4x2 + 2
4. Con la ayuda de una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y saca las conclusiones:
a. y = 2x2 + 3x – 2
b. y = -4x2 + 2x + 1
c. y = x2 + 5x - 1
d. y = -x2 + 3x - 4
5. Con la ayuda de una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y determine el vértice de cada una:
a. y = x2 + 4x
b. y = x2 – 2
c. y = -x2 + 2x + 1
d. y = x2 + 4x - 1
ACTIVIDAD
A. Graficar las siguientes funciones y ubicar el vértice en cada gráfica:
1. y = 3x2 – 1
2. y = -2x2 + 3
3. y = x2 - 2x - 3
4. y = x2 - 4x
B. Verifique la naturaleza de las raíces de las siguientes ecuaciones:
1. 3x2 – 6x +3 = 0
2. 6x2 + 7x + 2 = 0
3. 2x2 – 3x + 4 = 0
4. x2 – 2x – 24 = 0
C. Resuelve cada ecuación por raíz cuadrada.
1. 3x2 – 48 = 0
2. 4x2 – 100 = 0
3. 2x2 – 1 = 97
4. x2 + 2 = 11
5. x2 – 625 = 0
D. Resuelve cada ecuación por factorización.
1. x2 - 2x = 0
2. 2x2 + 4x = 0
3. 5x2 + 30x = 0
4. 3x2 = 15x
5. 4x2 = -20x
6. x2 + 5x + 6 = 0
7. x2 - 9x + 20 = 0
8. x2 + 12 = 7x
9. x2 - 2x = 3
10. 10 x2 + 19x + 6 = 0
E. Resuelve cada ecuación por fórmula general.
1. 2 x2 + 5x + 2 = 0
2. x2 + 4x + 3 = 0
3. x2 + 5x - 2 = 0
4. 2 x2 + 5x + 2 = 0

7.
INSTITUTO INTEGRADO CUSTODIO GARCÍA ROVIRA
Departamento de Matemáticas
Doc. Luis Fernando Waldo Martínez
3. Apoyándote en una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y saca las conclusiones:
a. y = 2x2 + 3
b. y = -3x2 + 1
c. y = -6x2 – 1
d. y = -1/4x2 + 2
4. Con la ayuda de una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y saca las conclusiones:
a. y = 2x2 + 3x – 2
b. y = -4x2 + 2x + 1
c. y = x2 + 5x - 1
d. y = -x2 + 3x - 4
5. Con la ayuda de una calculadora graficadora o de una computadora con software
graficador representa las siguientes funciones y determine el vértice de cada una:
a. y = x2 + 4x
b. y = x2 – 2
c. y = -x2 + 2x + 1
d. y = x2 + 4x - 1
ACTIVIDAD
A. Graficar las siguientes funciones y ubicar el vértice en cada gráfica:
1. y = 3x2 – 1
2. y = -2x2 + 3
3. y = x2 - 2x - 3
4. y = x2 - 4x
B. Verifique la naturaleza de las raíces de las siguientes ecuaciones:
1. 3x2 – 6x +3 = 0
2. 6x2 + 7x + 2 = 0
3. 2x2 – 3x + 4 = 0
4. x2 – 2x – 24 = 0
C. Resuelve cada ecuación por raíz cuadrada.
1. 3x2 – 48 = 0
2. 4x2 – 100 = 0
3. 2x2 – 1 = 97
4. x2 + 2 = 11
5. x2 – 625 = 0
D. Resuelve cada ecuación por factorización.
1. 2x2 - 10x = 0
2. 5x2 + 3x = 0
3. 12x2 + 30x = 0
4. 35x2 - 15x = 0
5. 6x2 = -42x
6. x2 = 5x
7. x2 + 11x + 30 = 0
8. x2 - 12 = -x
9. x2 + 5x = 14
10. 5 x2 + 14x + 8 = 0
E. Resuelve cada ecuación por fórmula general.
1. 2 x2 + 5x + 2 = 0
2. x2 + 4x + 3 = 0
3. x2 + 5x - 2 = 0
4. 2 x2 + 5x + 2 = 0