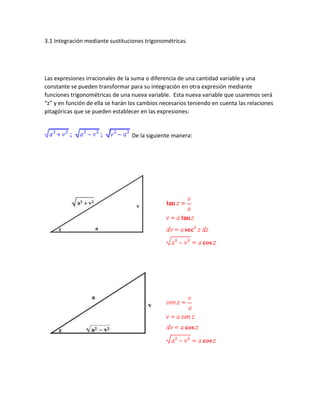
1. 3.1 Integración mediante sustituciones trigonométricas.
Las expresiones irracionales de la suma o diferencia de una cantidad variable y una
constante se pueden transformar para su integración en otra expresión mediante
funciones trigonométricas de una nueva variable. Esta nueva variable que usaremos será
“z” y en función de ella se harán los cambios necesarios teniendo en cuenta las relaciones
pitagóricas que se pueden establecer en las expresiones:
De la siguiente manera:

3. Problemas Propuest
2
2
2
2
2 2
2 2
2
2
25
; 5 5cos
5
25
cos ; 25 5cos
5
25
5cos 5cos cos sen
5 5 5 5 csc 5
5 sen
5 25 25
5ln csc 5cos 5ln 5
5
4
x dx
x
x
sen x sen dx d
x
x
x
tg
x
d d d d
d sen d
sen sen sen
x x
ctg c
x x
x dx
x
x
sen
   
 

       
   
   
  


  

  


     
 
      



     

2
2
2
2
2
2
2
2
2
; 2 2cos
2
4
cos ; 4 2cos
2
4
(2 ) 2cos 1 1
4 ( cos2 2 cos2 2 cos
2cos 2 2
4
2 2
25
; 5 5cos
5
25
cos ; 25 5cos
5
25
5
x sen dx d
x
x
x
tg
x
sen d
d sen
x x x
arcsen c
dx
x x
x
sen x sen dx d
x
x
x
tg
x
  
 

  
      

   
 

 

  


      

 

  

  


   

2
cos 1 1
csc d ln csc
5 5cos 5 5
1 5 25
ln
5
d
ctg c
sen
x
c
x x
 
   
 
   

  
 

4. 3.2 Integración por partes.
Cuando se desea integrar el producto de dos funciones, siendo estas funciones
diferenciales de la misma variable, es necesario recurrir a la integración por partes cuando
a dicho producto no se le puede integrar de otra manera, así tenemos entonces que si:
; luego
, y entonces:
que se llama fórmula de integración por partes.
Para aplicar la fórmula, debe descomponerse el integrando en dos factores que son:
y Debe aclararse que no hay una regla fija para determinar cuál de los dos factores es
y cual , por lo que solamente cabe hacer las siguientes indicaciones:
1.- El factor debe ser fácilmente integrable.
2.- debe ser más sencillo que
Problemas propuestos:
2 2 2cos 4 cos 2 cosx 8sen
2 2 2 2
2 ; 2
; 2cos
2 2
ln ln ln
ln ;
;
x x x x
xsen dx x dx x c
u x du dx
x x
dv sen v
xdx x x dx x x x c
dx
u x du
x
dv dx v x
      
 
  
    
 
 
 
 

5. Segundo caso
En algunas funciones, al integrar por partes, el integrando de es otra vez un
producto de dos funciones, de manera que nuevamente se integrará por partes esta
última expresión:
Problemas propuestos:
2 3 2 3 3
2
3 3
2 3 3 2 3 3 3
3 3
3 2 3 2 2 2
3 2
2 2
3 2
1 1
2
3 3
; 2
1
;
3
1 1 1 1 2
2 2
3 3 3 9 27
2 ; 2
1
;
3
1 3
2 2
; 3
1
;
2
1 3
2 2
x x x
x x
x x x x x
x x
x x x
x x
x
x e dx x e xe dx
u x du xdx
dv e v e
x e xe dx x e xe e c
u x du dx
dv e v e
x e dx x e x e
u x du x dx
dv e v e
x e
  
 
    
 
  
 
  
      
 
  
 
 
 

 

 
2 2 3 2 2 2 2
2
2 2
3 2 2 2 2 2 3 2 2 2 2 2
2 2
1 3 1 1
2 2 2 2
; 2
1
;
2
1 3 3 1 1 1 3 3 3
2 4 2 2 2 2 4 4 4
;
1
;
2
x x x x
x x
x x x x x x x x
x x
x e x e x e xe
u x du xdx
dv e v e
x e x e xe e dx x e x e xe e c
u x du dx
dv e v e
 
   
 
 
 
 
        
 
 
 
 

Tercer caso
Una de las aplicaciones más importantes de la integración por partes es el cálculo de la
integral de algunas expresiones que no tienen fórmula de integración inmediata,

6. 2 4 2 5 3 5 3
2
2 6 4 2 7 5 3 7 5 3
2 2
2
2 2
9 ( 9)*2 2 18 6 ( 9) 6( 9)
5 5
9; 9 ;2
1 2 ( 2 1) ( 2 1) ( 2 1)
2 1 ( ) * *
2 4 4 4 28 20 12 28 20 12
1
2 1; ;
2
x xdx a a ada a da a da a a c x x c
a x a x ada dx
a a da a da a da a a a x x x
x x a ada c
a
a x x ada dx
            
    
   
           

   
   
    
especialmente aquellas que se refieren a las funciones trigonométricas inversas. Para
integrar este tipo de funciones se siguen los mismos pasos que en los casos anteriores.
Una de las aplicaciones más importantes de la integración por partes es el cálculo de la
integral de algunas expresiones que no tienen fórmula de integración inmediata,
especialmente aquellas que se refieren a las funciones trigonométricas inversas. Para
integrar este tipo de funciones se siguen los mismos pasos que en los casos anteriores.
Problemas propuestos:
2
2
2
2
2
2
4 1
4 4 4 ln 1 16
1 16 8
4
4 ;
1 16
;v
sec sec sec ln 1
1
sec ;
1
;v
dx
arctg xdx xarctg x xarctg x x c
x
dx
u arctg x du
x
dv dx x
xdx
arc xdx xarc x xarc x x x
x x
dx
u arc x du
x x
dv dx x
     

 

 
     

 

 
 
 
3.3 Integración por sustituciones algebraicas.
Algunas integrales que no son inmediatas pueden resolverse fácilmente si se hacen
algunas sustituciones algebraicas convenientes.
Problemas propuestos

7. 3.4 Integración por fracciones parciales con denominadores lineales.
Si y son polinomios, entonces a la expresión se le denomina fracción
racional.
Si el grado de es menor que el grado de entonces a la fracción se le llama
propia. Es impropia Cuando el grado del numerador es de igual o mayor grado que el
denominador.
Algunos ejemplos de fracciones propias:
;
Algunos ejemplos de fracciones impropias:
;
Toda fracción propia puede escribirse como la suma de fracciones elementales de la
forma

8. Problemas propuestos
2 2
3 2
2
8 1 8 1
2 2 ( 2)( 1)( 1) 2 1 1
8 1 ( 1)( 1) B( 2)( 1) C( 2)( 1)
11 5
Resolviendo el sistema se obtiene que: , , 3
3 3
11 5 11
3 ln
3 2 3 1 1 3
t t dt t t dt Adt Bdt Cdt
t t t t t t t t t
t t t t t t t t
A B C
dt dt dt
t
t t t
   
   
        
          
   
      
  
    

2
2
1 2
5
2 ln 1 3ln 1
3
5 18 9
( 18) 18 4(5)(9) 18 12 3
; 3;
2(5) 5 5
( 3)(5 3) 3 5 3
1 (5 3) ( 3)
1 5
Resolviendo el sistema se obtiene que: ,
12 12
1 5 1
ln 3
12 3 12 5 3 12
t t c
dx
x x
x x x
dx Adx Bdx
x x x x
A x B x
A B
dx dx
x
x x
    
 
     
   
 
   
   
  
  
 
 

  

1
ln 5 3
12
x c  
Cuando se tienen n factores lineales iguales del denominador, les corresponde una suma
de fracciones de la siguiente forma:

9. Problemas propuestos:
3 2 2 2
2
2
3 5 3 5
1 ( 1)( 1) ( 1) ( 1) ( 1)
3 5 ( 1) ( 1)( 1) ( 1)
1 1
Resolviendo el sistema se obtiene que: , , 4
2 2
1 1 1 1 4
4 ln 1 ln 1
2 ( 1) 2 ( 1) ( 1) 2 2
x dx x dx Adx Bdx Cdx
x x x x x x x x
x A x B x x C x
A B C
dx dx dx
x x
x x x x
 
   
       
       
   
      
  
    
  
   4 4
3 3 2 2
4 2
1
8 8
2 ( 2) 2
8 (u 2) B(u 2) Cu
Resolviendo el sistema se obtiene que: 1, 4, 2
4
ln 2ln 2
c
u du u du Adu Bdu Cdu
u u u u u u u
u Au
A B C
u u c
u


 
   
  
     
   
   
    
3.5 Integración por fracciones parciales con denominadores cuadráticos.
Cuando los denominadores de las fracciones parciales son factores cuadráticos, los
numeradores deberán de tener la forma , siendo y constantes a
determinar.
Problemas propuestos:

10. 2 2
3 2 2
2
2
3 2 2
(5x 3) (5x 3)
( 1) 1
1 7 3
Resolviendo el sistema se obtiene que: , ,
2 2 2
1 7
3 7 32 2 ln 1 ln
1 2 2 2
4 4
4 ( 4) 4
Resolviendo el sist
x dx x dx Ax B C
x x x x x x
A B C
x dx
dx
x arctgx x c
x x
dx dx Ax B C
x x x x x x
    
  
  
  

     


  
  
   
 
   
2
2
1
ema se obtiene que: , 1, 1
2
1
1
12 ln 4 ln
4 2
A B C
x dx
dx
x x c
x x
  

    
 