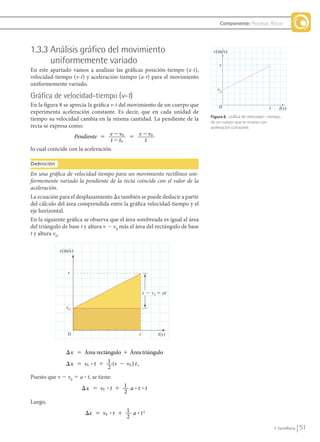
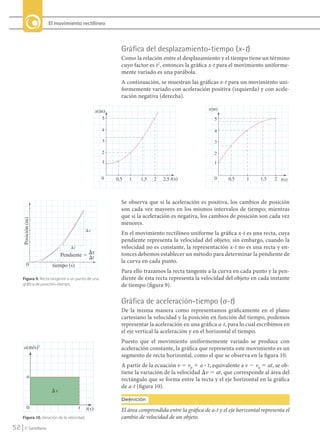
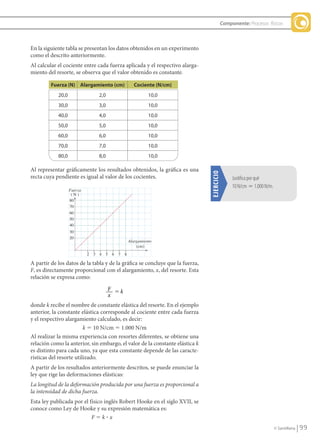
Este documento describe el análisis gráfico del movimiento uniformemente variado. Explica las gráficas de posición-tiempo (x-t), velocidad-tiempo (v-t) y aceleración-tiempo (a-t) para este tipo de movimiento. La gráfica v-t es una línea recta cuya pendiente es igual a la aceleración constante. La gráfica x-t es una parábola. La gráfica a-t es una línea horizontal ya que la aceleración es constante. También presenta un ejemplo numéric