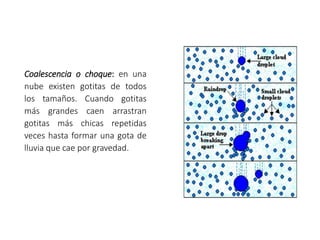
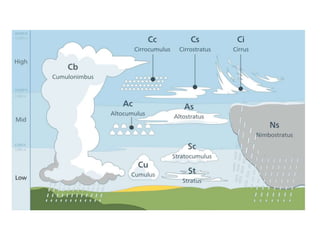
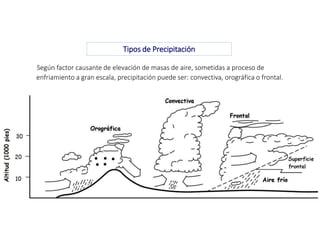
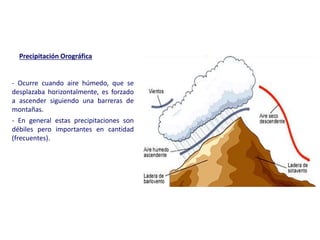
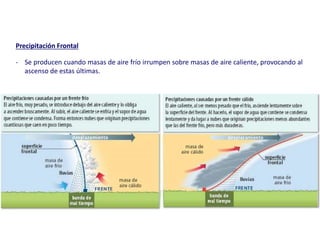
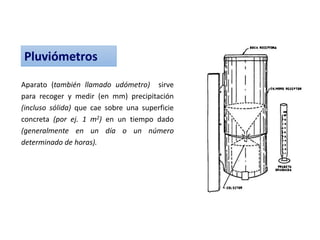
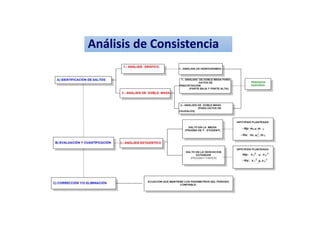
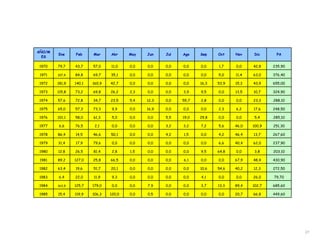
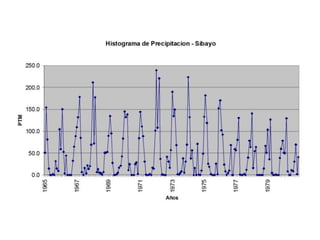
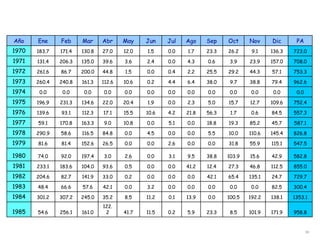
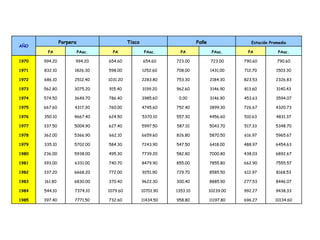
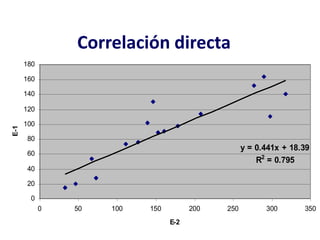
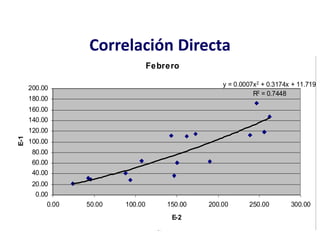
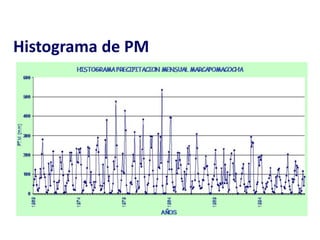
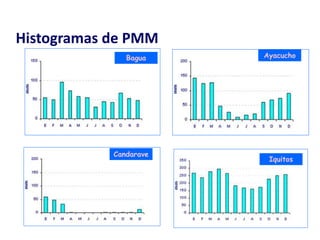
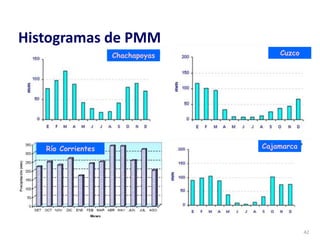
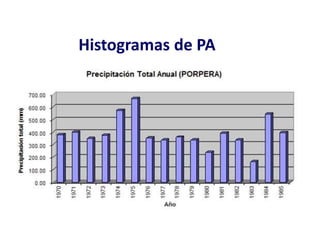
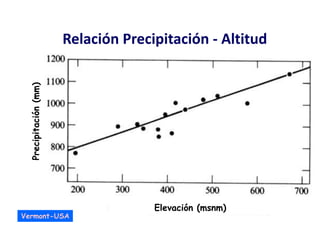
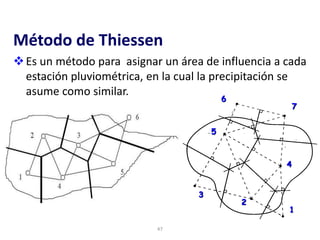
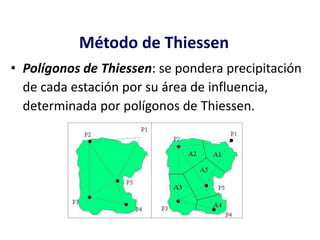
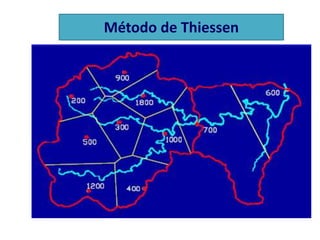
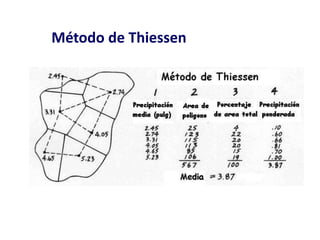
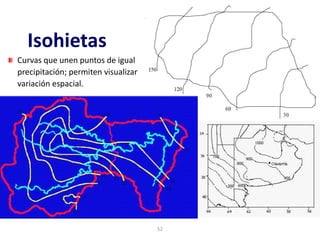
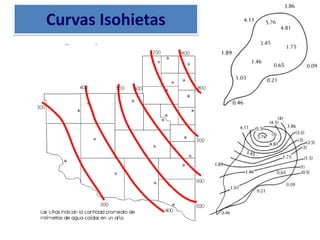
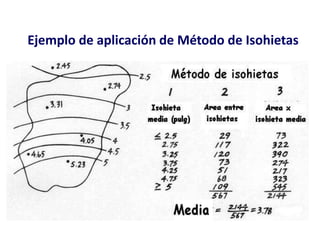
Este documento proporciona información sobre precipitación, incluyendo su definición, formación, tipos, medición y análisis. Brevemente resume: 1) La precipitación se refiere a agua que cae de la atmósfera en forma de lluvia, nieve u otros tipos. 2) Se forma a través de la condensación de vapor de agua en gotas de agua en las nubes. 3) Los tipos incluyen lluvia, granizo y nieve, y su medición se realiza con pluviómetros.

1. Huancayo - 2016
PRECIPITACION

2. Precipitación: nombre genérico dado a aguas meteóricas que provienen de
humedad atmosférica y que caen sobre superficie de Tierra.
Incluye: lluvia, granizo, nieve y rocío (vapor condensado directamente sobre
superficies frías).
Antes de alcanzar suelo interesa a meteorología; una vez que llega al suelo es elemento
básico de hidrología

3. 3
Formación: Producto de condensación se forman, en nubes, pequeñas
gotitas de agua (0,02 mm). Para que ocurra precipitación se deben
formar gotas de lluvia (2,0 mm), por:
- Atracción electrostática – tormentas eléctricas;
- Microturbulencia – vientos;
- Barrido de gotitas;
- Diferencia de temperatura;
- Núcleos de condensación (lluvia artificial)

4. Coalescencia o choque: en una
nube existen gotitas de todos
los tamaños. Cuando gotitas
más grandes caen arrastran
gotitas más chicas repetidas
veces hasta formar una gota de
lluvia que cae por gravedad.

5. Nubes
Masa de vapor con acumulación de pequeñas gotitas de agua o
pequeños cristales de hielo.
Clasificación (en función de su altura) :
a) Nubes altas: a más de 7 km. Son puro hielo, con T < -35°C; de
contornos indefinidos.
b) Nubes medias: entre 2 y 7 km; nubes mixtas de hielo y agua, con T >
-35°C.
c) Nubes bajas: por debajo de 2 km. Son nubes de agua con T de 0 a -
10°C y contornos perfectamente delimitados.

7. Formas de Precipitación
- Llovizna: gotas  < 0,5 mm; provenientes de masas con poca humedad y nubes bajas
y de poco espesor.
- Lluvia: gotas  > 0,5 mm; producida por nubes de varios km de espesor.
- Chubasco: inicio y final súbito; de corta duración (5 a 60 min.) ; gotas grandes;
producidas por nubes de gran extensión vertical y poca extensión horizontal.
- Granizo: trozos de hielo (pedrisco); 5 <  < 50 mm; producidas por nubes muy altas,
hasta 10 km.
- Rocío:  < 0,1 mm
- Escarcha: rocío helado.
- Niebla goteante.

8. Según factor causante de elevación de masas de aire, sometidas a proceso de
enfriamiento a gran escala, precipitación puede ser: convectiva, orográfica o frontal.
Tipos de Precipitación

9. Precipitación Convectiva
- Se origina por ascenso de masa de aire
caliente.
- La radiación solar provoca
calentamiento de superficie lo que hace
que el aire caliente con alto porcentaje de
vapor de agua se eleva verticalmente
- Típica de zonas tropicales o períodos
calurosos (verano)
- Tormentas localizadas, de fuerte
intensidad y corta duración.

10. Precipitación Orográfica
- Ocurre cuando aire húmedo, que se
desplazaba horizontalmente, es forzado
a ascender siguiendo una barreras de
montañas.
- En general estas precipitaciones son
débiles pero importantes en cantidad
(frecuentes).

11. Precipitación Frontal
- Se producen cuando masas de aire frío irrumpen sobre masas de aire caliente, provocando al
ascenso de estas últimas.

13. Conocida como Ridge A, la meseta antártica, está
localiza en el Territorio Antártico Australiano. Además de
ser el más seco, Ridge A es también el lugar más frío, con
una temperatura promedio en invierno de -70º C.

14. Record Guinness de lluvia en un sólo año
con 22.987 mm.

15. Lloró (Colombia) registra 13.300 mm
anuales.

16. En el monte Waialeale (Hawaii) llueve
360 días al año.

18. Se mide en lámina de agua que alcanzaría
a formarse sobre una superficie
impermeable.
Equipos de medición: pluviómetros y
pluviógrafos.
Interesa conocer su magnitud,
distribución, intensidad y probabilidad de
recurrencia de eventos de cierta
magnitud.
Medición de Precipitación

19. Pluviómetros
Aparato (también llamado udómetro) sirve
para recoger y medir (en mm) precipitación
(incluso sólida) que cae sobre una superficie
concreta (por ej. 1 m2) en un tiempo dado
(generalmente en un día o un número
determinado de horas).

20. Medición de Precipitación
Lectura pluviómetro
o Agua recogida en depósito se introduce en una probeta graduada, y se determina
cantidad de lluvia caída, es decir, altura en mm de capa de agua que se habría
podido formar sobre una superficie horizontal e impermeable, de no evaporarse
nada.
 Lectura se hace en horas sinópticas (7:00,
13:00 y 19:00), totalizando precipitación.

21. 1 m
1 m
1 m2
1 litro
1 mm
Pluviómetro
Cantidad de agua caída se expresa en mm y equivale a:
1 mm = 1 l/m2 = 10 m3/ha = 10000 l/ha = 1000 m3/km2
Medición de Precipitación

22. Procesamiento y Presentación de Datos Pluviométricos
 Existe diversidad de maneras de procesar y presentar datos pluviométricos de una estación o
representativos de una región.
 Elección del método depende de naturaleza de datos y del propósito que se tenga para su uso.
 Conjunto de datos (que representan altura de agua caída en horas, días, meses o años en un cierto
lugar) corresponde a una serie estadística y, en consecuencia, dicha serie es susceptible de analizar
y presentarse a través de métodos estadísticos.

23. Análisis de Precipitación
a) Análisis de consistencia, completación y extensión;
b) Análisis probabilístico de precipitación;
c) Análisis de variabilidad espacial y temporal de precipitación.

24. Análisis de Consistencia
• Proceso de identificación o detección, descripción y remoción de errores de
series de datos, a fin de obtener series confiables.
• Cambios naturales y antrópicos que afectan comportamiento hidrológico,
producen inconsistencia, representada como errores sistemáticos de saltos y
tendencias, y no homogeneidad, definida como el cambio brusco e
inesperado de datos con transcurso del tiempo.

25. Análisis de Consistencia

26. 26
Análisis Gráfico
• Análisis visual de distribución temporal de información hidrometeorológica, a fin de
detectar regularidad o irregularidad.
• Análisis de datos de precipitación, se efectúa con histogramas respectivos, donde
puede visualizarse ocurrencia de valores muy altos o bajos, saltos o tendencias.
• Histogramas, se utilizan para mostrar gráficamente comportamiento
hidrometeorológico que ocurre en una estación, en transcurso del tiempo.

27. 27
AÑO/M
ES
Ene Feb Mar Abr May Jun Jul Ago Sep Oct Nov Dic PA
1970 79,7 43,7 57,0 11,0 0,0 0,0 0,0 0,0 0,0 1,7 0,0 42,8 235,90
1971 107,4 84,8 69,7 35,1 0,0 0,0 0,0 0,0 0,0 5,0 11,4 63,0 376,40
1972 181,9 140,1 160,9 42,7 0,0 0,0 0,0 0,0 16,3 53,9 15,3 43,9 655,00
1973 115,8 73,2 69,8 26,2 2,3 0,0 0,0 3,9 9,5 0,0 13,5 10,7 324,90
1974 57,6 72,8 34,7 23,5 5,4 12,3 0,0 55,7 2,8 0,0 0,0 23,3 288,10
1975 65,0 57,3 73,3 9,9 0,0 16,9 0,0 0,0 0,0 2,3 6,2 17,6 248,50
1976 101,1 58,0 61,3 5,0 0,0 0,0 5,5 19,0 29,8 0,0 0,0 5,4 285,10
1977 6,6 76,5 2,1 0,0 0,0 0,0 3,2 3,2 7,2 5,6 46,0 100,9 251,30
1978 86,4 14,5 46,6 50,1 0,0 0,0 4,2 1,5 0,0 4,2 46,4 13,7 267,60
1979 31,4 17,9 79,6 0,0 0,0 0,0 0,0 0,0 0,0 6,6 40,4 62,0 237,90
1980 12,8 26,5 81,4 2,8 1,5 0,0 0,0 0,0 9,5 64,8 0,0 3,8 203,10
1981 89,2 127,0 25,8 66,5 0,0 0,0 0,0 6,1 0,0 0,0 67,9 48,4 430,90
1982 63,4 19,6 51,7 20,1 0,0 0,0 0,0 0,0 10,6 54,6 40,2 12,3 272,50
1983 6,4 22,0 11,9 9,3 0,0 0,0 0,0 0,0 4,1 0,0 0,0 26,0 79,70
1984 163,9 125,7 179,0 0,0 0,0 7,9 0,0 0,0 3,7 13,3 89,4 102,7 685,60
1985 15,4 119,9 106,3 120,0 0,0 0,5 0,0 0,0 0,0 0,0 20,7 66,8 449,60

29. - Denominado también de doble acumulación.
- Herramienta empleada en detección de inconsistencia en
datos hidrometeorológicos.
- Se compara datos de una estación particular, con los de una
estación probadamente consistente o con una ficticia, resultado del
promedio de estaciones en estudio, dentro de un área determinada
(Cuenca).
Análisis de Doble Masa

30. 30
Año Ene Feb Mar Abr May Jun Jul Ago Sep Oct Nov Dic PA
1970 183.7 171.4 130.8 27.0 12.0 1.5 0.0 1.7 23.3 26.2 9.1 136.3 723.0
1971 131.4 206.3 135.0 39.6 3.6 2.4 0.0 4.3 0.6 3.9 23.9 157.0 708.0
1972 261.6 86.7 200.0 44.8 1.5 0.0 0.4 2.2 25.5 29.2 44.3 57.1 753.3
1973 260.4 240.8 161.3 112.6 10.6 0.2 4.4 6.4 38.0 9.7 38.8 79.4 962.6
1974 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
1975 196.9 231.3 134.6 22.0 20.4 1.9 0.0 2.3 5.0 15.7 12.7 109.6 752.4
1976 139.6 93.1 112.3 17.1 15.5 10.6 4.2 21.8 56.3 1.7 0.6 84.5 557.3
1977 59.1 170.8 163.3 9.0 10.8 0.0 5.1 0.0 18.8 19.3 85.2 45.7 587.1
1978 290.9 58.6 116.5 84.8 0.0 4.5 0.0 0.0 5.5 10.0 110.6 145.4 826.8
1979 81.6 81.4 152.6 26.5 0.0 0.0 2.6 0.0 0.0 31.8 55.9 115.1 547.5
1980 74.0 92.0 197.4 3.0 2.6 0.0 3.1 9.5 38.8 103.9 15.6 42.9 582.8
1981 233.1 183.6 104.0 93.6 0.5 0.0 0.0 41.2 12.4 27.3 46.8 112.5 855.0
1982 204.6 82.7 141.9 33.0 0.2 0.0 0.0 0.0 42.1 65.4 135.1 24.7 729.7
1983 48.4 66.6 57.6 42.1 0.0 3.2 0.0 0.0 0.0 0.0 0.0 82.5 300.4
1984 301.2 307.2 245.0 35.2 8.5 11.2 0.1 13.9 0.0 100.5 192.2 138.1 1353.1
1985 54.6 256.1 161.0
122.
2 41.7 11.5 0.2 5.9 23.3 8.5 101.9 171.9 958.8

31. AÑO
Porpera Tisco Pañe Estación Promedio
PA PAac. PA PAac. PA PAac. PA PAac.
1970 994.20 994.20 654.60 654.60 723.00 723.00 790.60 790.60
1971 832.10 1826.30 598.00 1252.60 708.00 1431.00 712.70 1503.30
1972 686.10 2512.40 1031.20 2283.80 753.30 2184.30 823.53 2326.83
1973 562.80 3075.20 915.40 3199.20 962.60 3146.90 813.60 3140.43
1974 574.50 3649.70 786.40 3985.60 0.00 3146.90 453.63 3594.07
1975 667.60 4317.30 760.00 4745.60 752.40 3899.30 726.67 4320.73
1976 350.10 4667.40 624.50 5370.10 557.30 4456.60 510.63 4831.37
1977 337.50 5004.90 627.40 5997.50 587.10 5043.70 517.33 5348.70
1978 362.00 5366.90 662.10 6659.60 826.80 5870.50 616.97 5965.67
1979 335.10 5702.00 584.30 7243.90 547.50 6418.00 488.97 6454.63
1980 236.00 5938.00 495.30 7739.20 582.80 7000.80 438.03 6892.67
1981 393.00 6331.00 740.70 8479.90 855.00 7855.80 662.90 7555.57
1982 337.20 6668.20 772.00 9251.90 729.70 8585.50 612.97 8168.53
1983 161.80 6830.00 370.40 9622.30 300.40 8885.90 277.53 8446.07
1984 544.10 7374.10 1079.60 10701.90 1353.10 10239.00 992.27 9438.33
1985 397.40 7771.50 732.60 11434.50 958.80 11197.80 696.27 10134.60

32. S PPatrón
S PEstación
Criterio: valores acumulados de precipitación anual de una estación, graficados con los de
estación patrón, debe ser una línea recta (razón entre valores graficados no varía, por posibles
errores cometidos en toma y procesamiento de datos).
Si diagrama de doble
masa de una estación es
una línea recta, su
información analizada no
presenta errores, es
decir, es consistente.

33. 33
S PPatrón
S PEstación
Ma
Mo
 Presencia de quiebres
en recta de doble
masa, permite
establecer períodos de
probable información
dudosa.
Períodos más
largos y más
recientes serán
considerados
como confiables
ANALISISDOBLEMASA
0,0
200,0
400,0
600,0
800,0
1000,0
1200,0
0,0 200,0 400,0 600,0 800,0 1000,0 1200,0
PrecipitaciónAnualAcum.(Patrón)
PrecipitaciónAnualAcum.(Est.X)
Período
confiable
Período
confiabl
e
Período
dudoso
Períod
o
dudoso
Quiebr
e

34. Tarea.
Realizar el análisis grafico y análisis de doble masa con los datos de las estaciones de su cuenca.

35. • Completación y extensión de series de registros
hidrometeorológicos históricos consiste en determinar
correlación con registros coincidentes en estaciones vecinas.
• Estas últimas pueden referirse a otras medidas del mismo u
otro parámetro evaluado.
• Técnicas utilizadas: correlación directa, cruzada y
autocorrelación.
• Se requiere que estaciones estén ubicadas en lugares de
comportamiento similar.
Completación y extensión de información:
método de correlación

36. Correlación directa
y = 0.441x + 18.39
R2
= 0.795
0
20
40
60
80
100
120
140
160
180
0 50 100 150 200 250 300 350
E-2
E-1

37. 37
Correlación Directa
Febrero
y = 0.0007x2 + 0.3174x + 11.719
R2 = 0.7448
0.00
20.00
40.00
60.00
80.00
100.00
120.00
140.00
160.00
180.00
200.00
0.00 50.00 100.00 150.00 200.00 250.00 300.00
E-2
E-1

38. Análisis de Variabilidad
Variabilidad temporal:
Histogramas de PM: variabilidad estacional
Histogramas de PMM: variabilidad estacional
Histogramas de PA: variabilidad plurianual
Variabilidad espacial:
 Relación precipitación – altitud
 Mapas de isohietas
Precipitación media de cuenca:
Media aritmética
Isohietas
Polígonos de Thiessen

39. Variación temporal queda determinada por:
– Histogramas de PM, que proporcionan lámina de
precipitación mensual de cierto periodo de registro.
Permiten apreciar variabilidad estacional.
– Histogramas de PMM, que proporcionan lámina de
precipitación media mensual, obtenida a partir de un
registro histórico. Permiten apreciar variabilidad
estacional.
– Histogramas de PA, que muestran precipitación total
anual, a lo largo de un periodo de registro. Permiten
apreciar la variabilidad plurianual.
Variación Temporal

40. Histograma de PM

41. Histogramas de PMM
Bagua Ayacucho
Iquitos
Candarave

42. 42
Histogramas de PMM
Chachapoyas Cuzco
CajamarcaRío Corrientes

43. Histogramas de PA

44. 44
Variación geográfica:
 En términos generales, precipitación es máxima en zona
ecuatorial y decrece con latitud. Además, se ve influenciada
por efectos locales y por factores orográficos.
Variación Espacial
 Variación de precipitación media en mundo varía entre
distintas regiones. Zonas con <250 mm/año se consideran
desiertos; las que reciben >2000 mm/año son ecuatoriales o
tropicales.
 Al nivel de cuenca, variación espacial se analiza a través de
relación precipitación-altitud y de curvas isohietas

45. Relación Precipitación - Altitud
Vermont-USA
Elevación (msnm)
Precipitación(mm)

46. Precipitación Media en una Cuenca
• Media aritmética: es buena estimación si pluviómetros
están uniformemente distribuidos en cuenca (más o menos
plana, con precipitación poco variable, menor a 10%).
Ejemplo:

47. 47
Es un método para asignar un área de influencia a cada
estación pluviométrica, en la cual la precipitación se
asume como similar.
Método de Thiessen
5
2
4
3
7
6
1

48. Método de Thiessen
• Polígonos de Thiessen: se pondera precipitación
de cada estación por su área de influencia,
determinada por polígonos de Thiessen.

49. 49
Método de Thiessen
Procedimiento:
Se une estaciones mediante rectas.
Se levantan mediatrices de rectas.
Se define polígonos por mediatrices y divisoria de aguas.
Se determina precipitación media de cuenca.

50. Método de Thiessen

51. Método de Thiessen

52. 52
Isohietas
Curvas que unen puntos de igual
precipitación; permiten visualizar
variación espacial.

53. Método de Isohietas
 Método más preciso que consiste en trazar curvas de
igual precipitación (isoyetas).
 Luego, se determina áreas entre isoyetas, que
constituirán pesos de ponderación en cálculo de
precipitación media.

















 






1i,i
1i,i
1ii
A
A
2
PP
P
 En trazo de isoyetas debe considerarse efectos de colinas y
montañas en distribución en área de precipitación (efectos
orográficos).
 Fórmula de precipitación media en una cuenca:
Pi – precipitación correspondiente a
isoyeta “i”
Pi+1 – precipitación correspondiente a
isoyeta i+1
Ai,i+1 – área entre isoyetas i e i+1

54. Curvas Isohietas

55. Ejemplo de aplicación de Método de Isohietas

56. GRACIAS