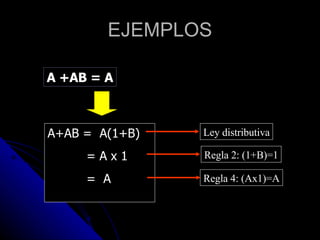
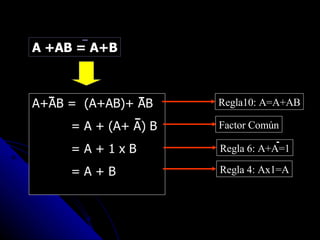
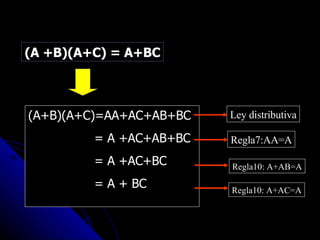
Este documento presenta una introducción al álgebra de Boole. Explica que el álgebra de Boole es una herramienta para modelar sistemas digitales y que se basa en la lógica y el razonamiento humano. Define funciones binarias como la unión, la intersección y la negación, y presenta leyes como la conmutativa, asociativa y distributiva. También muestra ejemplos de cómo aplicar las reglas del álgebra de Boole para simplificar expresiones.

1. ALGEBRA DE BOOLE CAMILA ANDREA CARDOZO. CODIGO: 20910188

6. EJEMPLOS A +AB = A A+AB = A(1+B) = A x 1 = A Ley distributiva Regla 2: (1+B)=1 Regla 4: (Ax1)=A

7. A +AB = A+B A+AB = (A+AB)+ AB = A + (A+ A) B = A + 1 x B = A + B Regla10: A=A+AB Factor Común Regla 6: A+A=1 Regla 4: Ax1=A

8. (A +B)(A+C) = A+BC (A+B)(A+C)=AA+AC+AB+BC = A +AC+AB+BC = A +AC+BC = A + BC Ley distributiva Regla7:AA=A Regla10: A+AB=A Regla10: A+AC=A

9. COMO SIMPLIFICAR CON LAS REGLAS DE BOOLE? 1) ab + a(b+c) + b (b+c) = ab + ab + ac + b + bc = ab + ac + b (1+ c) = ab + ac + b  1 = ab + ac + b = b (a +1) + ac = b  1 + ac = b +ac 2) [ab  (c+bd) +ab]c = [abc+ 0 + ab]c = abc + abc = (a + a) bc = 1  bc = bc Regla 2 Regla 4

10. GRACIAS