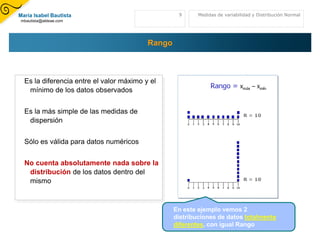
El documento aborda las medidas de variabilidad y la distribución normal, enfatizando la importancia de la validez y confiabilidad en los procedimientos de medición para obtener datos precisos. Se definen conceptos clave como la dispersión, varianza y desviación estándar, destacando su papel en la interpretación de la variabilidad de los datos. Además, se menciona la relevancia de la distribución normal en la estadística, sirviendo como un modelo para diversos fenómenos naturales y sociales.

1. Medidas de variabilidad y Distribución NormalComprender el significado de las Medidas de variabilidad

2. Comprender el significado de la Distribución NormalValidez y confiabilidadUn procedimiento de medición será confiable en la medida en que proporciona datos con poca variación.

3. Si el proceso es válido mide lo que se desea medir, por tanto disponer de un procedimiento de medición válido y confiable será muy deseable.

4. Por ejemplo, una prueba con elevada confiabilidad y validez medirá el conocimiento que se pretende evaluar de manera repetible cuando se aplique una y otra vez.Un procedimiento de medición que sea confiable proporciona datos con poca variación2Medidas de variabilidad y Distribución Normal

5. Dispersión¿Cuánto se alejan los datos de la Media que es igual a 6?Calificaciones obtenidas en el examen de Inglés, escala del 0 al 10

6. DispersiónSi la media µx = 6La dispersión es la media de la diferencia entre cada valor y la mediaLa suma de las desviaciones respecto a la media siempre es igual a cero

7. DispersiónLas medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central denominado Media

8. Distinguimos entre medidas de dispersión absolutas, que no son comparables entre diferentes muestras y las relativas que nos permitirán comparar varias muestras.Media5Medidas de variabilidad y Distribución Normal

9. VariaciónSi se mide cierta propiedad de dos objetos o sucesos, los resultados pueden ser diferentes. Tal variación ocurre de modo natural y por eso se denominan “variables”

10. La problemática de la variación se complica al reconocer que ella también ocurre en quienes miden y en los instrumentos: encuestas, exámenes, etc. que se usan para medir.

11. En esta sesión estudiaremos las medidas de variación que indican cuan alejados pueden estar los valores de la media. Esto nos ayuda a:Calibrar el análisis de mas medidas de tendencia centralCuestionar el valor de la muestraJuzgar la confiabilidad de las medidas de tendencia central. Si los datos están muy dispersos las medidas de TC no son representativas de los datos de la muestra como un todoMedia6Medidas de variabilidad y Distribución Normal

12. VariaciónEn el caso estudiado de sesiones anteriores, Nota final promedio obtenida en Física 9º de una muestra de 25 instituciones privadas del Distrito Capital

13. ¿Qué factores pueden afectar la media obtenida?Calidad y experiencia de los docentes de cada centro.El número de horas de estudioEl número de estudiantes por aula de clase.Recursos Tecnológicos del centro de estudioEstrategias de enseñanza7Medidas de variabilidad y Distribución Normal

14. Una vez localizado el centro de la distribución de frecuencias (Me) de un conjunto de datos, el siguiente paso es buscar una medida de la variabilidad o dispersión de los datos, ya que es importante conocer si los valores en general están cerca o alejados de los valores centrales.Las medidas de variación o dispersión son:Rango

15. Varianza

16. Desviación estándar

17. Coeficiente de VariaciónMedidas de variación o dispersiónµ8Medidas de variabilidad y Distribución Normal

18. RangoEs la diferencia entre el valor máximo y el mínimo de los datos observadosEs la más simple de las medidas de dispersiónSólo es válida para datos numéricosNo cuenta absolutamente nada sobre la distribución de los datos dentro del mismoEn este ejemplo vemos 2 distribuciones de datos totalmente diferentes, con igual Rango9Medidas de variabilidad y Distribución Normal

19. La Varianza S2 Interpretación:La varianza mide la mayor o menor dispersión de los valoresde la variable respecto a la media aritmética.

20. Cuanto mayor sea la varianza mayor dispersiónexistirá y por tanto menor representatividad tendrá la media aritmética.

21. La varianza se expresa en las mismas unidades que la variable analizada, pero elevadas al cuadrado.

22. La varianza siempre es mayor o igual que ceroy menor que infinito La Varianza (S2) de los datos es la medida de dispersión más utilizada. ¿Cómo calcularla?Es la media de los cuadrados de las diferencias entre cada valor de la variable (xi) y la media aritmética (X) de la distribución.S210Medidas de variabilidad y Distribución NormalNomenclatura: S2 o