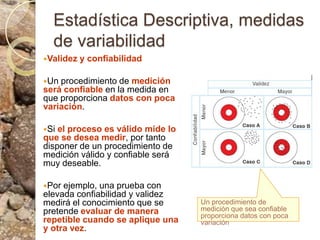
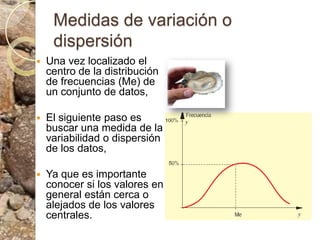
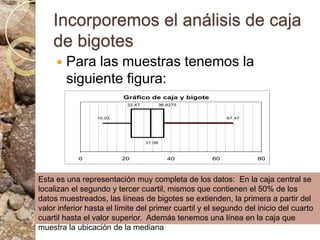
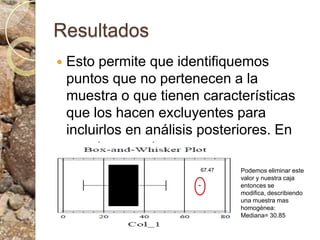
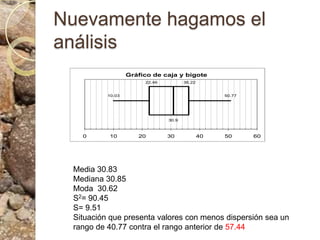
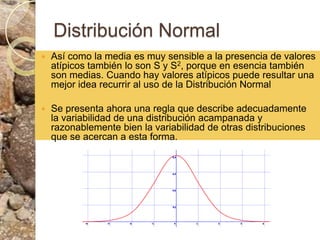
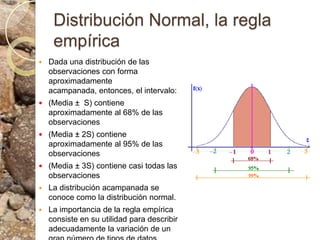
Este documento discute conceptos estadísticos como variabilidad, varianza, desviación estándar y distribución normal. Explica que la varianza y desviación estándar miden qué tan dispersos están los valores respecto al promedio. Calcula estas medidas para datos de longitud de ostras, encontrando una desviación estándar de 10.09. También analiza los datos usando una caja de bigotes e identifica un valor atípico. Finalmente, presenta la regla empírica de la distribución normal.

1. DispersiónEstadística CIMACODr. Carlos Cáceres Martínez, presentación preparada a partir del trabajo de la Dra. María Isabel Bautista mbaitista@aldeae.com

2. Estadística Descriptiva, medidas de variabilidadValidez y confiabilidadUn procedimiento de medición será confiable en la medida en que proporciona datos con poca variación. Si el proceso es válido mide lo que se desea medir, por tanto disponer de un procedimiento de medición válido y confiable será muy deseable.Por ejemplo, una prueba con elevada confiabilidad y validez medirá el conocimiento que se pretende evaluar de manera repetible cuando se aplique una y otra vez.Un procedimiento de medición que sea confiable proporciona datos con poca variación

3. VariaciónSi se mide cierta propiedad de dos objetos o sucesos, los resultados pueden ser diferentes. Tal variación ocurre de modo natural y por eso se denominan “variables”La problemática de la variación se complica al reconocer que ella también ocurre en quienes miden y en los instrumentos: encuestas, exámenes, etc. que se usan para medir.En esta sesión estudiaremos las medidas de variación que indican cuan alejados pueden estar los valores de la media. Esto nos ayuda a:Calibrar el análisis de mas medidas de tendencia centralCuestionar el valor de la muestraJuzgar la confiabilidad de las medidas de tendencia central. Si los datos están muy dispersos las medidas de TC no son representativas de los datos de la muestra como un todoLas medidas de dispersión cuantifican la separación, la dispersión, la variabilidad de los valores de la distribución respecto al valor central. Distinguimos entre medidas de dispersión absolutas, que no son comparables entre diferentes muestras y las relativas que nos permitirán comparar varias muestras.

4. VariaciónTamaño de la muestra.La experiencia de los estudiantes que realizaron el muestreo para desprender ostiones.El tiempo que dedicaron los estudiantes a tomar la muestra.Los cuchillos y espátulas con que se recolectaron los ostiones.La estrategia de muestreo; su planeaciónEn el caso estudiado la muestra de la población de ostiones Sacrosstreapalmuladel malecón de La Paz, BCS, México de 144 individuos medidos en su longitud (distancia antero posterior 0.01 mm)¿Qué factores pueden afectar la media obtenida?

5. Medidas de variación o dispersiónUna vez localizado el centro de la distribución de frecuencias (Me) de un conjunto de datos, El siguiente paso es buscar una medida de la variabilidad o dispersión de los datos, Ya que es importante conocer si los valores en general están cerca o alejados de los valores centrales.

6. Medidas de variabilidad, la Varianza S2Interpretación:La varianza mide la mayor o menor dispersión de los valores de la variable respecto a la media aritmética. Cuanto mayor sea la varianza mayor dispersión existirá y por tanto menor representatividad tendrá la media aritmética.La varianza se expresa en las mismas unidades que la variable analizada, pero elevadas al cuadrado. La varianza siempre es mayor o igual que cero y menor que infinito Existen distintas formas de cuantificar la variabilidad, pero la Varianza (S2) de los datos es la más utilizada. Es la media de los cuadrados de las diferencias entre cada valor de la variable (xi) y la media aritmética (X) de la distribución.S2 =

7. Medidas de variabilidad, Desviación estándar SEs la medida de variabilidad utilizada con más frecuencia en la investigación por ser la más estable de todas y se basa en los desvíos de los datos originales con respecto a la media x. Se define como la raíz cuadrada con signo positivo de la varianza.Corrige la posible distorsión del valor obtenido en la Varianza (S2), producto de la sumatoria de las diferencias al cuadrado del valor de las observaciones menos la media aritmética, es decir:

8. Calculemos la S2 y la S de los datos de ostión:Para ello hagamos uso de las herramientas de excel, en análisis de datos o bien de las funciones estadísticas obteniendo: Media 30.54 Mediana 31.08 Moda 30.62 y ahora Varianza de la muestra 101.82 Desviación estándar 10.09

9. Y ¿que significa esto?Media 30.54Desvío máximo 67.47-30.54Desvío mínimo 30.54- 10.03Longitud en mm del ostión medidas individualesEl valor de la desviación estándar es: S=10.09 unidades de la media.Interpretación: Cuando los valores de un conjunto de observaciones están muy próximos a su Media (30.54), la dispersión es menor que cuando están distribuidos sobre un amplio recorrido. Una Varianza pequeña nos indica que la variable no se desvía "demasiado" de su media , que es "poco" probable que haya valores alejados de la media, o dicho de otra manera que es "muy" probable que los valores se encuentren alrededor de la media.

10. Incorporemos el análisis de caja de bigotesPara las muestras tenemos la siguiente figura:Esta es una representación muy completa de los datos: En la caja central se localizan el segundo y tercer cuartil, mismos que contienen el 50% de los datos muestreados, las líneas de bigotes se extienden, la primera a partir del valor inferior hasta el límite del primer cuartil y el segundo del inicio del cuarto cuartil hasta el valor superior. Además tenemos una línea en la caja que muestra la ubicación de la mediana

11. Podemos ir mas allá:Resulta que si alguno de los puntos sean los mínimos o los máximos se encuentran a una distancia superior a 1.5 veces el intervalo del intercuartil por encima o debajo de la caja (recordemos que contiene el 50% de los datos) entonces podemos señalarlos en esté gráfico con una marca (un cuadrado), y en caso de que los puntos se encuentren a una distancia de 3.0 veces el intervalo del cuartil podemos marcarlos con un signo adicional.

12. ResultadosEsto permite que identifiquemos puntos que no pertenecen a la muestra o que tienen características que los hacen excluyentes para incluirlos en análisis posteriores. En nuestro caso tenemos:67.47Podemos eliminar este valor y nuestra caja entonces se modifica, describiendo una muestra mas homogénea:Mediana= 30.85

13. Nuevamente hagamos el análisisMedia 30.83Mediana 30.85Moda 30.62S2= 90.45S= 9.51Situación que presenta valores con menos dispersión sea un rango de 40.77 contra el rango anterior de 57.44

14. Distribución NormalAsí como la media es muy sensible a la presencia de valores atípicos también lo son S y S2, porque en esencia también son medias. Cuando hay valores atípicos puede resultar una mejor idea recurrir al uso de la Distribución NormalSe presenta ahora una regla que describe adecuadamente la variabilidad de una distribución acampanada y razonablemente bien la variabilidad de otras distribuciones que se acercan a esta forma.

15. Distribución Normal, su importanciaInsistiremos en la distribución normal, cuya relevancia en estadística se debe a que muchos fenómenos físicos, biológicos, psicológicos y sociológicos, pueden ser adecuadamente representados mediante ella. La distribución normal es también una buena aproximación de otras distribuciones, como la Binomial, Poisson y T de Student, para ciertos valores de sus parámetros.Una buena cantidad de mediciones de características de seres vivos y otras variables que se observan en la naturaleza siguen una distribución en forma de campana u otra forma similar a ésta.

16. Distribución Normal, la regla empíricaDada una distribución de las observaciones con forma aproximadamente acampanada, entonces, el intervalo:(Media ± S) contiene aproximadamente al 68% de las observaciones(Media ± 2S) contiene aproximadamente al 95% de las observaciones(Media ± 3S) contiene casi todas las observacionesLa distribución acampanada se conoce como la distribución normal. La importancia de la regla empírica consiste en su utilidad para describir adecuadamente la variación de un gran número de tipos de datos.

17. Distribución Normal, la regla empíricaPara describir los datos se calculan los intervalos para cada grupo de valores(X±S ) = (X±2S ) =(X±3S ) =De acuerdo con la regla empírica se espera que los valores sean para cada grupo: aproximadamente el 68% de las observaciones estarán en el intervalo de _____________

18. 95% de las observaciones estarán en el intervalo de ___________