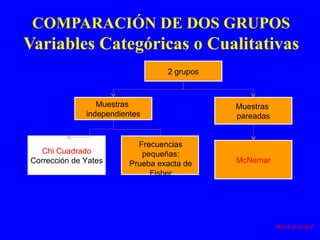
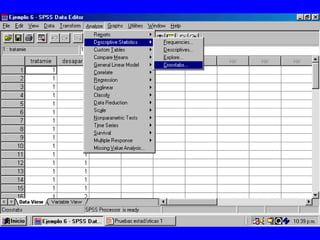
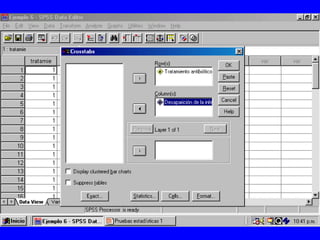
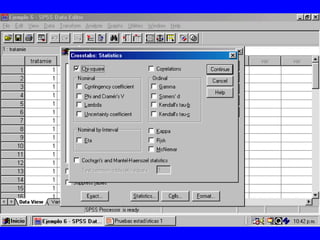
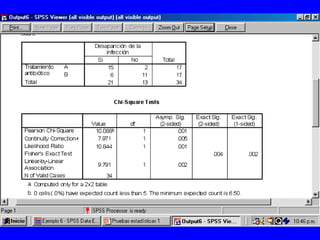
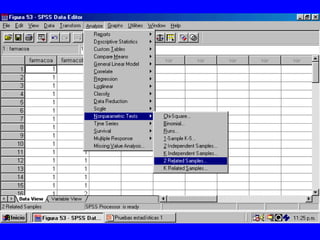
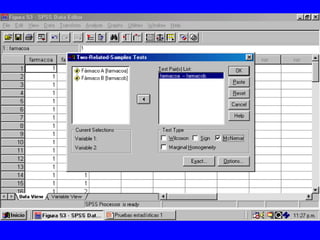
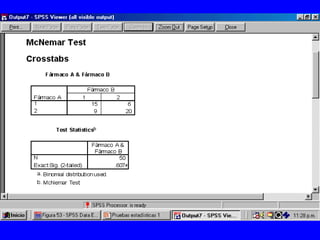
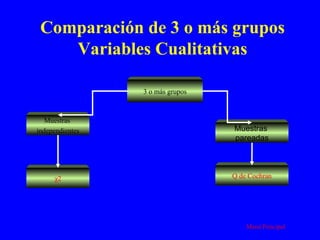
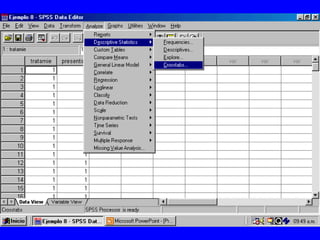
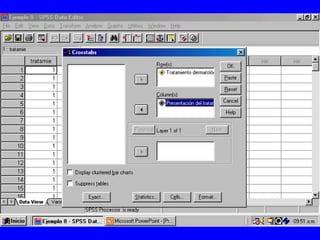
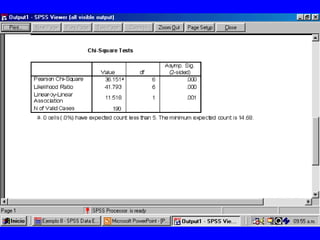
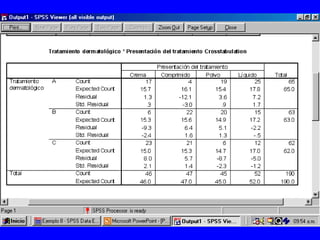
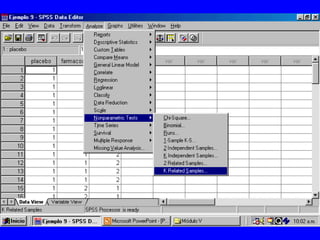
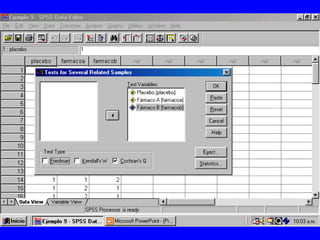
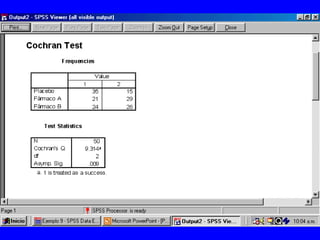
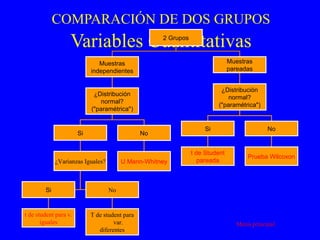
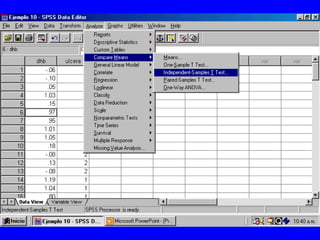
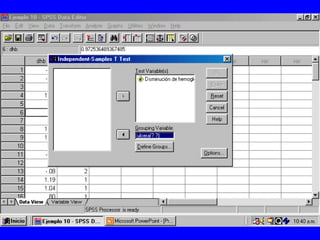
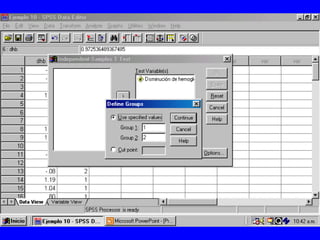
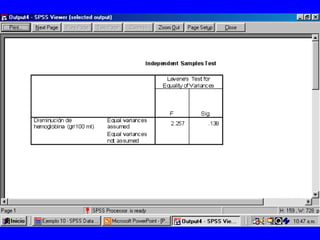
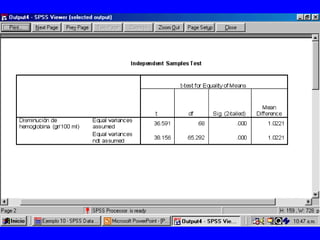
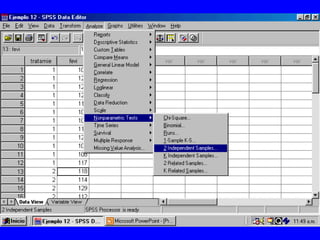
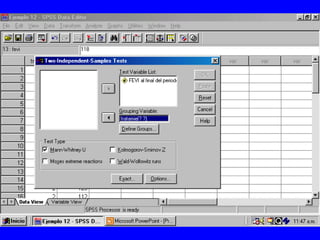
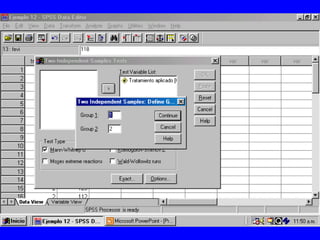
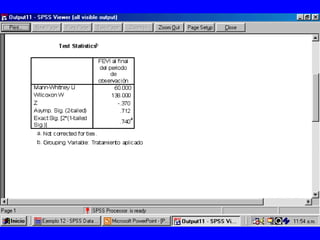
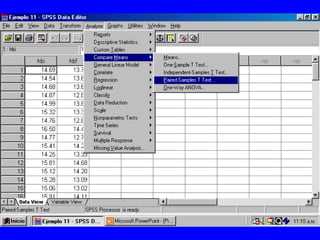
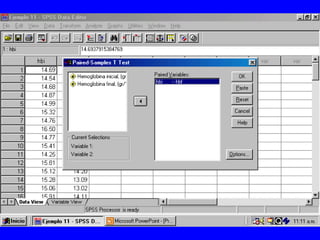
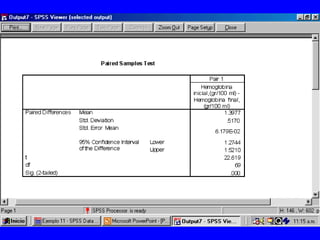
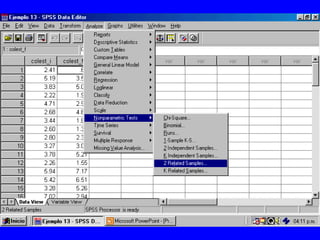
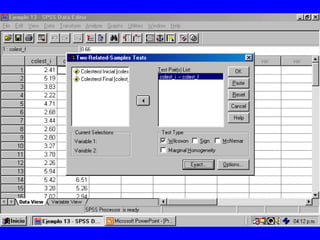
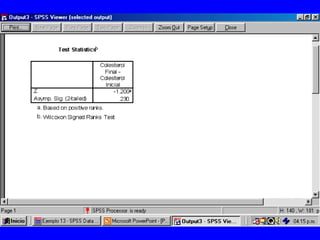
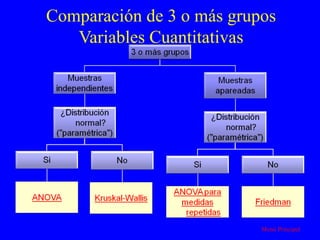
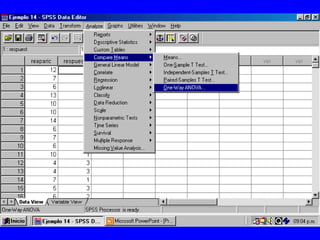
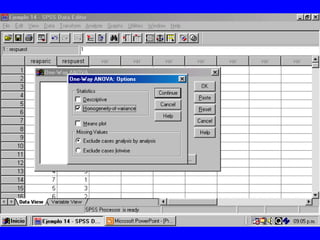
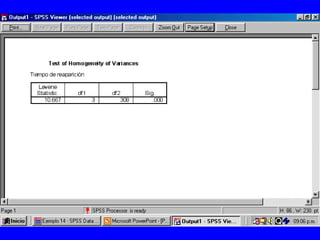
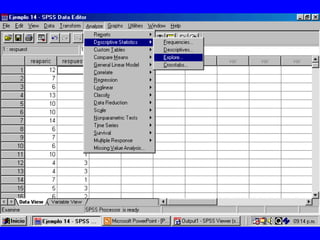
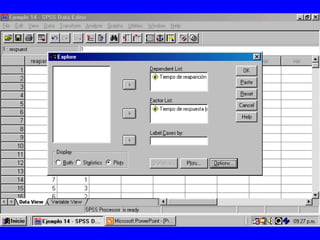
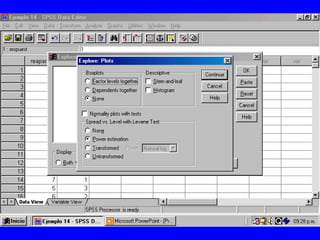
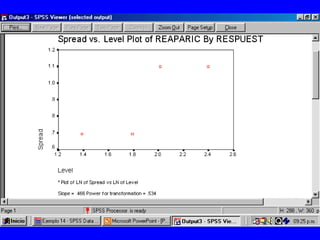
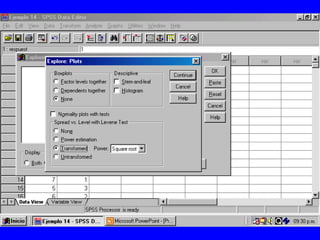
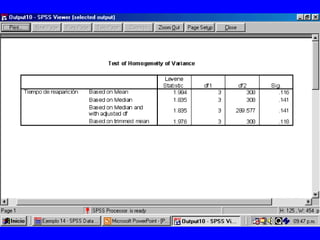
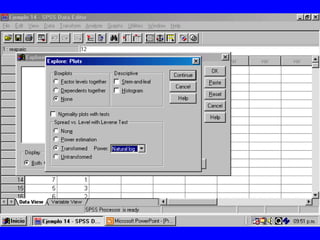
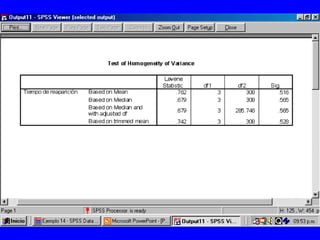
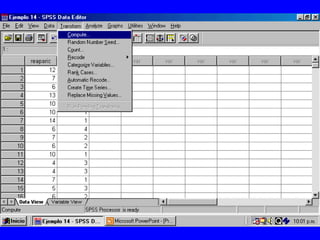
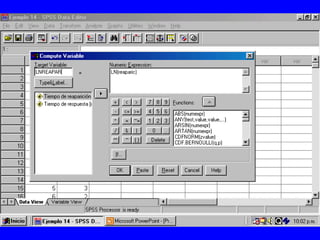
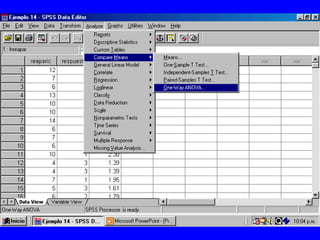
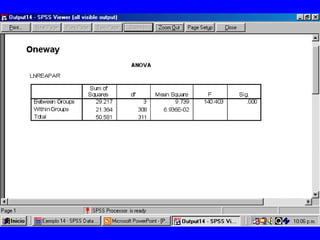
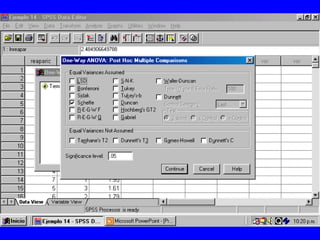
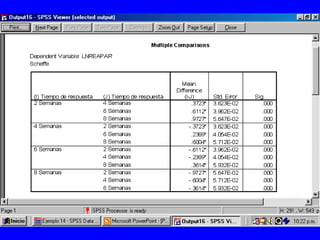
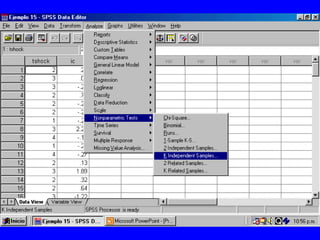
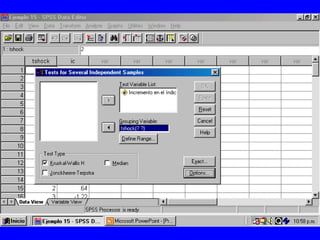
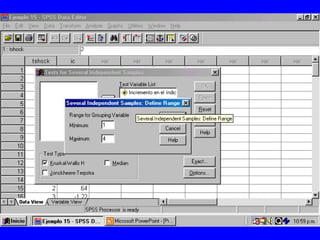
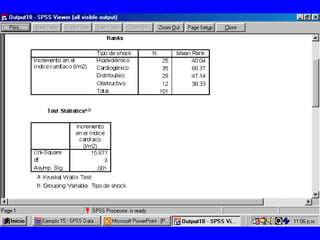
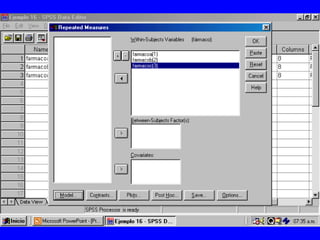
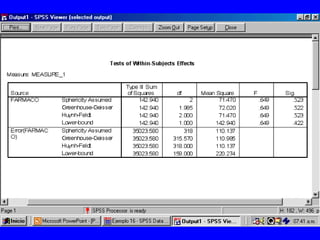
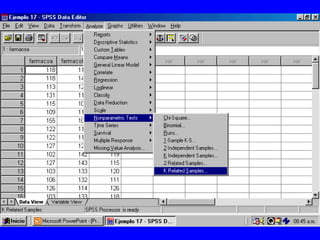
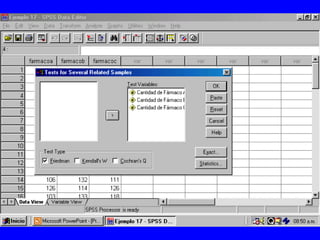
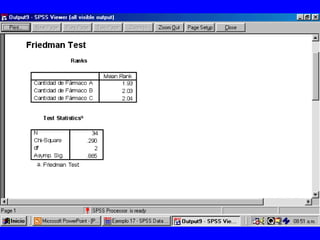
El documento trata sobre conceptos básicos de bioestadística para la realización y análisis de pruebas de hipótesis. Explica el significado del valor de p y cómo interpretarlo, la diferencia entre muestras independientes y pareadas, la importancia de probar la normalidad de los datos antes de seleccionar pruebas paramétricas o no paramétricas, y ejemplos de cómo utilizar pruebas estadísticas como la t de Student, U de Mann-Whitney y Chi cuadrado en SPSS para comparar grupos con variables cual

1. BIOESTADÍSTICA

2. Prueba de Hipótesis Consideraciones preliminares El valor de “p” Muestras independientes o pareadas Varianzas iguales o diferentes Prueba de la normalidad Datos fuera de rango Pruebas paramétricas o no paramétricas

3. EL VALOR DE “p” … sea cual sea el valor de “p” y demasiadas veces de “ No hay diferencias significativas” deducimos que “no hay diferencias”. Austin Bradford Hill

4. … el valor de “p” El valor de “p” nos permitirá interpretar los resultados de un análisis de datos realizado por un software, toda vez que en este caso ya no existe la necesidad de usar tablas para comparar un valor calculado con el tabulado .

5. … el valor de “p” Interpretación: Si el valor de “p” es mayor que el valor de significación ( α ) entonces no existen diferencias estadísticamente significativas . Si el valor de “p” es menor que el valor de significación ( α ) entonces existen diferencias estadísticamente significativas.

6. Muestras Independientes o Pareadas Muestras Independientes Se dice que dos o más muestras son independientes cuando sus datos provienen de grupos diferentes, que no guardan ninguna relación entre sí. Ejm. Proporción de muertes neonatales de los hospitales de Essalud y Minsa. IMC de madres adolescentes de Lima Cuadrada y Chosica. Edad gestacional de Adolescentes y Añosas.

7. … muestras Independientes o Pareadas Muestras Pareadas o Repetidas Se dice que las muestras son pareadas cuando Dos o más grupos de datos provienen de una misma muestra, también se denomina muestra repetida. Ejm. Cuando se quieren determinar diferencias entre los niveles de Hb en una intervención quirúrgica en tres momentos :Hb basal, a los 10 minutos y a los 20 minutos.

8. Cuando se forman dos muestras en donde las personas son pareadas o emparejadas con otras personas que tienen las mismas características que se desean controlar. Ejm. Se quiere determinar si el hecho de comer pescado es un factor para contraer el cólera. Para lo cual se identifica a un grupo de personas que tuvieron la enfermedad y se emparejan cada una de ellas con otra persona que no tiene la enfermedad. Se empareja tomando en cuenta ciertos tipos de variables, edad, sexo, barrio,etc. … muestras Independientes o Pareadas

9. Prueba de la Normalidad Es importante realizar esta prueba cuando no se tiene la certeza de que los datos provienen o no de una curva normal. Conocer si los datos provienen de una curva normal permitirá decidir que pruebas se han de utilizar. Se utilizarán pruebas Paramétricas si los datos provienen de una curva normal. Se utilizarán pruebas No paramétricas si los datos no provienen de una curva normal.

10. … prueba de la Normalidad La condición para decidir si un determinado grupo de datos tiende a una curva normal es que al menos existan más de 30 datos de la variable en estudio (tamaño de muestra mínimo) en cada grupo de estudio.

11. De particular interés están los coeficientes de asimetría y curtosis estandarizados que pueden utilizarse para determinar si la muestra procede de una distribución normal. Los valores de estos estadísticos fuera del rango de -2 a +2 indican alejamiento significante de normalidad que tendería a invalidar cualquier test estadístico con respecto a la desviación normal. … prueba de la Normalidad

12. También se puede utilizar el valor de Asimetría para la prueba de la normalidad. Si el valor de Asimetría es mayor que 1(uno) en valor absoluto entonces se dice que no pertenece a una distribución normal. … prueba de la Normalidad

13. En algunos casos a pesar de que existe una gran cantidad de datos (más de 30), sin embargo los valores de curtosis o asimetría indican que los datos no provienen de una curva normal. Esto se puede deber a la presencia de datos FUERA DE RANGO O INTERVALO. Datos Fuera de Rango o Intervalo

14. El dato se observa, registra e introduce en la computadora incorrectamente. El dato proviene de una población distinta. El dato es correcto pero representa un suceso poco común (fortuito). Datos Fuera de Rango o Intervalo Los datos fuera de intervalo aparecen generalmente por las siguientes razones:

15. Como detectar un dato fuera de rango Calculando el Valor Z Si el valor de Z es mayor de 3 quiere decir que ese dato está fuera de intervalo, ya que se asume que el 100% de una población está comprendida dentro del rango de -3z y +3z (-3s y +3s).

16. 2. Con el gráfico de Caja y Bigotes ( Box and Plot ). Al elaborar este gráfico haciendo uso de los rangos intercuartílicos y la mediana, así como los valores de -3s y +3s. Se puede determinar fácilmente los datos que se encuentran fuera de rango.

17. Transformación a curva normal Los datos que no cumplen el criterio de ser una curva normal de acuerdo con los anteriores estadísticos, se pueden convertir a una curva normal utilizando la raíz cuadrada o el logaritmo natural de los datos.

18. Pruebas Paramétricas o No Paramétricas Pruebas Paramétricas Se dice que una prueba es paramétrica cuando: Se trata de variables cuantitativas cuyo número es mayor de 30 datos o provienen de una curva normal. Pueden ser menos de 30 datos si es que se tiene la seguridad que provienen de una curva normal Si son seis o menos datos, usar pruebas no paramétricas. Algunos indican 11 o menor de 20.

19. … Pruebas Paramétricas o No Paramétricas Pruebas no Paramétricas Son pruebas no paramétricas cuando: Se trata de variables cualitativas. Se trata de variables cuantitativas, con menos de 30 datos y no provienen de una curva normal. Cuando son seis o menos datos. Algunos indican 11 o 20 datos.

20. SPSS

21. PRUEBAS ESTADÍSTICAS Pruebas para Comparar grupos Variables cualitativas Variables cuantitativas 2 grupos 3 grupos 2 grupos Tres o más grupos

22. Pruebas para comparar grupos VARIABLES CUALITATIVAS

23. COMPARACIÓN DE DOS GRUPOS Variables Categóricas o Cualitativas Menú principal 2 grupos Muestras independientes Chi Cuadrado Corrección de Yates Frecuencias pequeñas: Prueba exacta de Fisher Muestras pareadas McNemar

24. Comparación de dos proporciones Independientes Prueba de Chi Cuadrado Ejemplo 6 Se desea analizar el tratamiento de la infección urinaria con dos antibióticos A y B. Dividiéndose 34 pacientes en dos grupos de 17, evaluándose después de un tiempo de observación si la infección desapareció o no.

25. Solución Codificar la variable 1 como: Etiqueta: Tratamiento de Antibiótico 1= A 2= B Codificar la variable 2 como Etiqueta: Desaparición de la Infección 1= Si 2= No

30. Interpretación Como el valor de p = 0,001 es menor que 0,05 entonces hay diferencias significativas entre los grupos, por lo tanto podemos concluir que el tratamiento con el antibiótico A es más eficaz que el antibiótico B. volver

31. Comparación de dos proporciones pareadas Prueba de Chi Cuadrado de McNemar Ejemplo 7 Se desea saber si el efecto de dos fármacos es el mismo para desaparecer los síntomas de una úlcera. Para lo cual se seleccionan 50 pacientes a los que se les administra el fármaco A. Luego se busca a otro paciente de características similares (Par o “gemelo”) al que se les suministra el fármaco B. Después de un periodo de observación se comprueba en cada caso si los síntomas han desaparecido.

32. Solución Codificar la variable 1 como: Etiqueta: Fármaco A 1= Úlcera ha cicatrizado 2= Úlcera no ha cicatrizado Codificar la variable 2 como Etiqueta: Fármaco B 1= Úlcera ha cicatrizado 2= Úlcera no ha cicatrizado

36. Interpretación Como el valor de p = 0,607 es mayor que 0,05 entonces no hay diferencias significativas entre los grupos, por lo tanto podemos concluir que el Fármaco A y el Fármaco B tienen la misma eficacia para la cicatrización de úlceras. Volver

37. Comparación de 3 o más grupos Variables Cualitativas Menú Principal Muestras independientes Muestras pareadas 3 o más grupos χ 2 Q de Cochran

38. Comparación de 3 o más proporciones Independientes Prueba de Chi Cuadrado Ejemplo 8 Se desea analizar si el efecto de tres tratamientos dermatológicos para el acné A,B y C, depende del tipo de presentación, crema, comprimido, polvo y líquido. Para lo cual se distribuyen 300 pacientes en 12 grupos de 25 cada uno. Luego de un periodo de observación se analiza la proporción de pacientes sin acné en cada grupo. Se desea determinar si la eficacia del tratamiento está relacionado con el tipo de presentación.

39. Solución Codificar la variable 1 como: Etiqueta: Tratamiento dermatológico 1= A 2= B 3= C Codificar la variable 2 como Etiqueta: Presentación del tratamiento 1= Crema 2= Comprimido 3= Polvo 4= Líquido

46. Interpretación Como el valor de p = 0,00 asociado al estadístico Chi cuadrado es menor que 0,05 entonces hay diferencias significativas entre los grupos, por lo tanto podemos concluir que el uso del tratamiento dependerá del tipo de presentación. Volver

47. Comparación de 3 o más proporciones pareadas Prueba Q de Cochran Ejemplo 9 Se desea analizar el efecto de dos fármacos sobre los síntomas de la úlcera, para lo cual se distribuyen 150 pacientes en tres grupos de 50 cada uno. Aleatoriamente se suministra a 50 pacientes un placebo, luego se busca dos pares o “gemelos” a quienes se les suministra los fármacos A y B respectivamente. Después de un periodo se observa si los síntomas han desaparecido o no. Se desea determinar si la eficacia de los fármacos con respecto al placebo es la misma .

48. Solución Codificar la variable 1 como: Etiqueta: Placebo 1= Úlcera ha cicatrizado 2= Úlcera no ha cicatrizado Codificar la variable 2 como Etiqueta: Fármaco A 1= Úlcera ha cicatrizado 2= Úlcera no ha cicatrizado Codificar la variable 3 como: Etiqueta: Fármaco B 1= Úlcera ha cicatrizado 2= Úlcera no ha cicatrizado

52. Interpretación Como el valor de p = 0,09 asociado al estadístico Q de Cochran es menor que 0,05 entonces hay diferencias significativas entre los grupos, por lo tanto podemos concluir que los fármacos tienen menor efectividad que el placebo. Volver

53. Pruebas para comparar grupos VARIABLES CUANTITATIVAS

54. COMPARACIÓN DE DOS GRUPOS Variables Cuantitativas Menú principal 2 Grupos Muestras independientes ¿Distribución normal? ("paramétrica") Si ¿Varianzas Iguales? Si t de student para v. iguales No T de student para var. diferentes No U Mann-Whitney Muestras pareadas ¿Distribución normal? ("paramétrica") Si t de Student pareada No Prueba Wilcoxon

55. Comparación de dos grupos independientes con distribución normal Prueba de t de Student Ejemplo 10 Se desea conocer si la disminución de hemoglobina es independiente de la presencia o no de úlcera en los pacientes cuando se aplica un nuevo tratamiento. Para lo cual se mide la disminución de hemoglobina en 70 pacientes, de los cuales 28 tenían úlcera y 42 no.

56. Solución Codificar la variable 1 como: Etiqueta: Disminución de Hemoglobina Codificar la variable 2 como Etiqueta: Con úlcera 1= Si 2= No

61. El valor de p= 0,138 nos indica que no hay diferencias significativas entre las varianzas por lo que se asume la igualdad de varianzas.

63. Interpretación Como el valor de p= 0,00 asociado al estadístico “t”, cuando se asumen varianzas iguales es menor que 0,05 entonces existen diferencias significativas entre los promedios. Por lo tanto se puede concluir que la disminución de hemoglobina es diferente entre los pacientes con úlcera y sin úlcera. Para el ejemplo existe mayor disminución de hemoglobina en los pacientes con úlcera. Volver

64. Comparación de dos grupos independientes sin distribución normal (no paramétrica) Prueba de U de Mann- Witney Ejemplo 12 Se desea conocer si al aplicar un nuevo Fármaco más el tratamiento habitual permite incrementar la FEVI (fracción de eyección del ventrílocuo izquierdo) deprimida en grado severo. Se seleccionan 12 pacientes a los que se les aplica el tratamiento habitual y 11 pacientes a quienes se les aplica el tratamiento habitual más el nuevo Fármaco. Luego de seis meses se mide la FEVI en ambos grupos.

65. Solución Codificar la variable 1 como: Etiqueta: FEVI Codificar la variable 2 como Etiqueta: Tratamiento 1= Habitual 2= Habitual más fármaco.

70. Interpretación Como el valor de p= 0,740 asociado al estadístico “U” de Mann-Whitney, es mayor que 0,05 entonces no existen diferencias significativas entre las muestras. Por lo tanto se puede concluir que el uso del Farmaco A más el tratamiento habitual no aumenta significativamente el FEVI. Volver

71. Comparación de dos grupos pareados con distribución normal Prueba de t de Student para muestras pareadas Ejemplo 11 Se desea conocer si un tratamiento contra la artrosis puede causar disminución de hemoglobina. Para lo cual se mide la hemoglobina en 70 pacientes antes y después del tratamiento.

72. Solución Codificar la variable 1 como: Etiqueta: Hemoglobina inicial Codificar la variable 2 como Etiqueta: Hemoglobina final

76. Interpretación Como el valor de p= 0,00 asociado al estadístico “t”, es menor que 0,05 entonces existen diferencias significativas entre los promedios inicial y final. Por lo tanto se puede concluir que el tratamiento contra la artrosis produce disminución de hemoglobina. Volver

77. Comparación de dos grupos pareados sin distribución normal Prueba de Wilcoxon Ejemplo 13 Se desea conocer si el nivel de colesterol se incrementa debido a un producto (A) presente en la dieta de los pacientes de un hospital. Para lo cual se cambia el Producto A por un producto B menos rico en colesterol y se hace la medición del colesterol a 42 pacientes antes y después de la sustitución del producto.

78. Solución Codificar la variable 1 como: Etiqueta: Colesterol inicial Codificar la variable 2 como Etiqueta: Colesterol final

82. Interpretación Como el valor de p= 0,230 asociado al estadístico Wilcoxon, es mayor que 0,05 entonces existen diferencias significativas entre los rangos positivos y negativos. Por lo tanto se puede concluir que el colesterol en los pacientes no se ve incrementado por el consumo del producto A. volver

83. Comparación de 3 o más grupos Variables Cuantitativas Menú Principal

84. Comparación de 3 o más grupos independientes con distribución normal ANÁLISIS DE LA VARIANZA (ANOVA) Ejemplo 14 Se desea saber si el tiempo de reaparición de los síntomas en pacientes con úlcera péptica es independiente del tiempo de respuesta a un tratamiento aplicado. Para lo cual se determina el tiempo de reaparición de los síntomas y se agrupa de acuerdo al tiempo de respuesta en cuatro grupos (2, 4, 6 y 8 semanas).

85. Solución Codificar la variable 1 como: Etiqueta: Tiempo de respuesta al tratamiento 1 = 2 semanas 2 = 4 semanas 3 = 6 semanas 4 = 8 semanas Codificar la variable 2 como Etiqueta: Tiempo de reaparición de los síntomas

89. Como el valor de p = 0,00 asociado al estadístico de Levene es menor que 0,05 entonces las varianzas son diferentes, por lo que se tendrá que homogenizar las varianzas con la función potencia, raíz cuadrada y logaritmo natural.

102. Interpretación Como el valor de p = 0,00 asociado al estadístico de F de Snedecor es menor que 0,05 entonces existen diferencias significativas entre los promedios. Por lo tanto se tiene que realizar la prueba de comparaciones múltiples para determinar entre que grupos existen las diferencias. Tukey (grupos del mismo tamaño) Scheffé (grupos de diferente tamaño)

105. Conclusión El análisis de comparaciones múltiples nos indica que todos los grupos son diferentes, por lo tanto se debe considerar que el tiempo de reaparición de los síntomas va a ser diferente para cada tiempo de respuesta al tratamiento. volver

106. Comparación de 3 o más grupos independientes sin distribución normal ANÁLISIS DE LA VARIANZA DE KRUSKAL-WALLIS Ejemplo 15 Se desea saber si un Fármaco aumenta el índice cardiaco en pacientes con Shock, pero se sospecha que el aumento puede ser diferente según el tipo de shock. Para lo cual se suministra el fármaco a 99 pacientes y después de un determinado tiempo se mide el índice cardiaco y se divide en cuatro grupos de acuerdo con el tipo de shock (Hipovolémico, Cardiogénico, Distributivo y Obstructivo).

111. Interpretación Como el valor de p = 0,001 es menor que 0,05 entonces los promedios de rangos en los cuatro tratamientos son diferentes. Por lo tanto se puede concluir indicando que el fármaco incrementa el índice cardiaco independientemente del tipo de shock. Siendo mayor el efecto en el grupo cardiogénico. Volver

112. Comparación de 3 o más grupos pareados con distribución normal ANOVA PARA MEDIDAS REPETIDAS Ejemplo 16 Se desea conocer el efecto de tres fármacos para reducir la presión arterial sistólica. Para lo cual se buscó a 160 pacientes, a los que se les administró el fármaco A, luego se buscó a dos “pares” o “gemelos” de la misma edad, al primero se le administró el Fármaco B y al segundo el Fármaco C.

113. Solución Codificar la variable 1 como: Etiqueta: Fármaco A Codificar la variable 2 como Etiqueta: Fármaco B Codificar la variable 3 como Etiqueta: Fármaco C

119. Interpretación Como el valor de p = 0,523 asociado al estadístico de contraste es mayor que 0,05 entonces no existen diferencias significativas entre los grupos. Por lo tanto se puede concluir que el efecto de los fármacos sobre la presión arterial sistólica es el mismo. Volver

120. Comparación de 3 o más grupos pareados sin distribución normal PRUEBA DE FRIEDMAN Ejemplo 17 Se desea conocer si el consumo de un fármaco (A) antihipertensivo es igual que el de otros dos fármacos (B y C) de la competencia. Para lo cual se seleccionan aleatoriamente 34 farmacias y se obtiene el número de fármacos (A, B y C) vendidos en el mes en cada farmacia.

121. Solución Codificar la variable 1 como: Etiqueta: Cantidad de Fármaco A Codificar la variable 2 como: Etiqueta: Cantidad de Fármaco B Codificar la variable 3 como: Etiqueta: Cantidad de Fármaco C

125. Interpretación Como el valor de p = 0,865 asociado al estadístico de Friedman es mayor que 0,05 entonces no existen diferencias significativas entre los grupos. Por lo tanto se puede concluir que la venta de los tres fármacos es la misma. volver

126. Asociación entre dos variables cuantitativas Correlación de Pearson Ejemplo 21 Se realiza un estudio para establecer una ecuación mediante la cual se pueda utilizar la concentración de estrona en saliva ( X ) para predecir la concentración del esteroide en plasma libre ( Y ). Para lo cual se midieron la concentración de ambos indicadores en 14 varones sanos.

127. Solución Codificar la variable 1 como: Etiqueta: Estrona en Saliva Codificar la variable 2 como: Esteroide en plasma libre

132. Interpretación Como el valor de p = 0,00 asociado al estadístico t es menor que 0,05 entonces podemos concluir que conociendo el nivel de estrona en la saliva se puede predecir concentración de esteroide en el plasma libre. VOLVER

133. Volver Figura 4. Ejemplo de gráfico de Caja y Bigotes. Edad de encuestados.