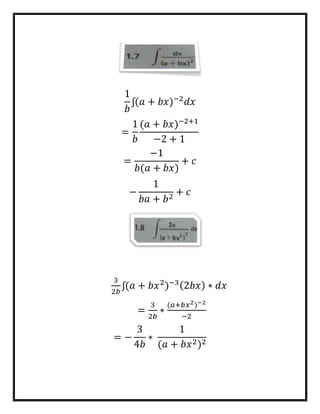
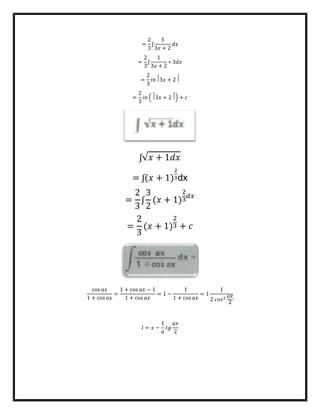
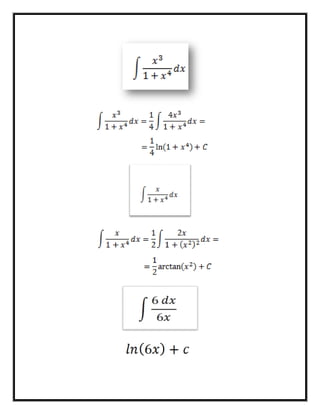
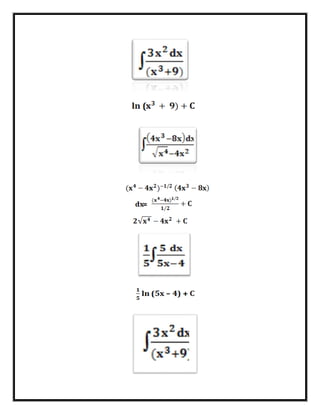
El documento presenta varias fórmulas para el cálculo integral. Explica que la integral de una función representa el área bajo la curva definida por la función entre dos límites y que es la operación inversa de la derivada. Luego enumera seis fórmulas comunes para calcular integrales definidas e indefinidas de funciones como polinomios, exponenciales, logaritmos y trigonométricas.

1. Calculo integral
Utilización de la formulas
(1,2,3,4,5,6)
Marco Abraham Saldaña Originales
30/09/2018

2. Introducción:
La integral de una función F consiste en el área bajo la
curva delimitada por los extremos de esta y sus
proyecciones sobre uno de los ejes. La integración es
un concepto fundamental del análisis matemático y las
ecuaciones diferenciales, Básicamente, una integral es
una suma de infinitos sumandos, infinitamente
pequeños. La integral de una función arroja datos
relevantes de áreas determinadas por curvas y formas
aun no concluidas. También para determinar solidos
generados a partir de la revolución de ellos. Este
proceso es considerado la anti-derivada de la función,
ya que revoca cualquier efecto producido por la
diferenciación de la función provocando así que una
función derivada regrese a su estado y forma original.

4. FÓRMULA 1
ʃ𝑑𝑥 = 𝑥 + 𝑐
= x+c
= f(x)+c
= 𝑘 ʃ 𝑓( 𝑥) 𝑑𝑥
=f(x)+c

5. = 5𝑥4
+ 𝑐
= 𝑒 𝑥
+ 𝑐
FÓRMULA 2
ʃ𝑥 𝑛
𝑑𝑥 =
𝑥 𝑛+1
𝑛 + 1
+ 𝑐

6. 1
𝑏
ʃ(𝑎 + 𝑏𝑥)−2
𝑑𝑥
=
1
𝑏
(𝑎 + 𝑏𝑥)−2+1
−2 + 1
=
−1
𝑏(𝑎 + 𝑏𝑥)
+ 𝑐
−
1
𝑏𝑎 + 𝑏2
+ 𝑐
3
2𝑏
ʃ(𝑎 + 𝑏𝑥2
)−3(2𝑏𝑥) ∗ 𝑑𝑥
=
3
2𝑏
∗
(𝑎+𝑏𝑥2)−2
−2
= −
3
4𝑏
∗
1
(𝑎 + 𝑏𝑥2)2

7. −
3
4𝑥 ∗ (𝑎 + 𝑏𝑥2)2
+ 𝑐
5
12
ʃ(4𝑥3
+ 3)
−1
7 ∗ (12𝑥2) 𝑑𝑥
=
5
12
(4𝑥3
+ 3)
−1
7
+1
−
1
7
+ 1
=
35
72
(4+3)
6
7+c
2ʃ(1 + √ 𝑥
1
2
1
2√ 𝑥
𝑑𝑥
= 𝟐
(𝟏 + √ 𝒙
𝟏
𝟐
+ 𝟏
𝟏
𝟐 + 𝟏
=
𝟒
𝟑
(𝟏 + √ 𝒙
𝟐
𝟑 + 𝒄

8. 1
6
ʃ53𝑥2+1(6𝑥) 𝑑𝑥
53𝑥2+1
6𝑖𝑛(5)
+ 𝑐
FÓRMULA 3
ʃ (
𝑎 𝑥+1
𝑎 𝑥 𝑏 𝑥
+
𝑏 𝑥−1
𝑎 𝑥 𝑏 𝑥
) 𝑑𝑥
ʃ (
a
bx
+
1
axb
) dx
= ʃ(𝑎𝑏−𝑥
+
1
𝑏
𝑎−𝑥)
𝑑𝑥 = −𝑎ʃ𝑏−𝑥(−1)𝑑𝑥 −
1
𝑏
ʃ𝑎−𝑥(−1)𝑑𝑥 = −𝑎
𝑏−𝑥
log 𝑏
−
1
𝑏
∗
𝑥−1
log 𝑎

9. =
b−x
log b
−
1
b
∗
x−1
log a
+c
ʃ
𝑎2𝑥+𝑏2+2𝑎 𝑥 𝑏 𝑥
𝑎 𝑥 𝑏 𝑥 dx
ʃ (
𝑎 𝑥
𝑏 𝑥
+
𝑏 𝑥
𝑎 𝑥
+ 2) 𝑑𝑥 = ʃ (
𝑎 𝑥
𝑏 𝑥
+
𝑏 𝑥
𝑎 𝑥
+ 2) 𝑑𝑥
= ʃ((
𝑎
𝑏
) + (
𝑏
𝑎
) 𝑥
+ 2) 𝑑𝑥
= 2𝑥
(
𝑎
𝑏
) 𝑥
𝑙𝑜𝑔
𝑎
𝑏
+
(
𝑏
𝑎
) 𝑥
𝑙𝑜𝑔
𝑏
𝑎
+ 𝑐
ʃ𝑒2𝑥∗𝑙𝑜𝑔3
∗ 𝑒−4𝑥∗𝑙𝑜𝑔5
𝑑𝑥
= ʃ𝑒 𝑥(2𝑙𝑜𝑔3 𝑙𝑜𝑔5)
𝑑𝑥 =
1
2𝑙𝑜𝑔3 − 4
ʃ𝑒 𝑥(2𝑙𝑜𝑔3−4𝑙𝑜𝑔5)
(2𝑙𝑜𝑔3 − 4𝑙𝑜𝑔5)𝑑𝑥
1
2𝑙𝑜𝑔3 − 4𝑙𝑜𝑔5
𝑒 𝑥(2𝑙𝑜𝑔3−4𝑙𝑜𝑔5)
=
1
log(32 ∗ 5−4)
32𝑥∗5−4𝑥
+ 𝑐

10. ʃ𝑒2𝑥
∗ 39
∗ 52
𝑑𝑥
ʃ32𝑥
∗ 5−4
𝑑𝑥 = ʃ39
∗ 52
1
log(32 ∗ 5−4)
32𝑥
∗ 5−4𝑥
+ 𝑐
ʃ
𝑒 𝑥
+ 𝑒2𝑥
1 + 𝑒2𝑥
𝑑𝑥 = ʃ
𝑒 𝑥
1 + (𝑒 𝑥)2
𝑑𝑥 + ʃ
62𝑥
1 + 𝑒2𝑥
𝑑𝑥 = 𝑎𝑟𝑐 𝑡𝑔 𝑒 𝑥
+
1
2
log(1 + 𝑒2𝑥
)
= 𝑎𝑟𝑐 𝑡𝑔 𝑒 𝑥
+
1
2
log(1 + 𝑒2𝑥
)+c
FÓRMULA 4
ʃ𝑎𝑎𝑣 = 𝑎ʃ𝑎𝑣

11. ʃ (
1
𝑥2
+
1
𝑥√ 𝑥
+ 5) 𝑑𝑥 = ʃ
1
𝑥2
𝑑𝑥 + ʃ
1
𝑥√ 𝑥
𝑑𝑥 + ʃ5𝑑𝑥
ʃ
1
𝑥2
ʃ𝑥−2
𝑑𝑥 =
1
𝑥2
𝑑𝑥ʃ𝑥−2
𝑑𝑥
=
1
(−2 + 1) 𝑑𝑥
=
ʃ(−2 + 1)𝑥−2
𝑑𝑥
−
1
𝑥
−
2
√ 𝑥
+ 5 + 𝑐
ʃ
2
3𝑥 + 2
𝑑𝑥 = 2ʃ
1
3𝑥 + 2
𝑑𝑥

12. =
2
3
ʃ
3
3𝑥 + 2
𝑑𝑥
=
2
3
ʃ
1
3𝑥 + 2
∗ 3𝑑𝑥
=
2
3
𝑖𝑛⃒3𝑥 + 2⃒
=
2
3
𝑖𝑛 (⃒3𝑥 + 2⃒) + 𝑐
ʃ√𝑥 + 1𝑑𝑥
= ʃ(𝑥 + 1)
2
3dx
=
2
3
ʃ
3
2
(𝑥 + 1)
2
3
𝑑𝑥
=
2
3
(𝑥 + 1)
2
3 + 𝑐
cos 𝑎𝑥
1 + cos 𝑎𝑥
=
1 + cos 𝑎𝑥 − 1
1 + cos 𝑎𝑥
= 1 −
1
1 + cos 𝑎𝑥
= 1
1
2 𝑐𝑜𝑠2 𝑎𝑥
2
𝑙 = 𝑥 −
1
𝑎
𝑡𝑔
𝑎𝑥
2

13. FÓRMULA 5
ʃ𝑣 𝑛
𝑑𝑣 =
𝑣 𝑛+1
𝑛 + 1
+ 𝑐

16. FÓRMULA 6

18. 1
3
𝑖𝑛( 𝑥3
+ 9) + 𝑐