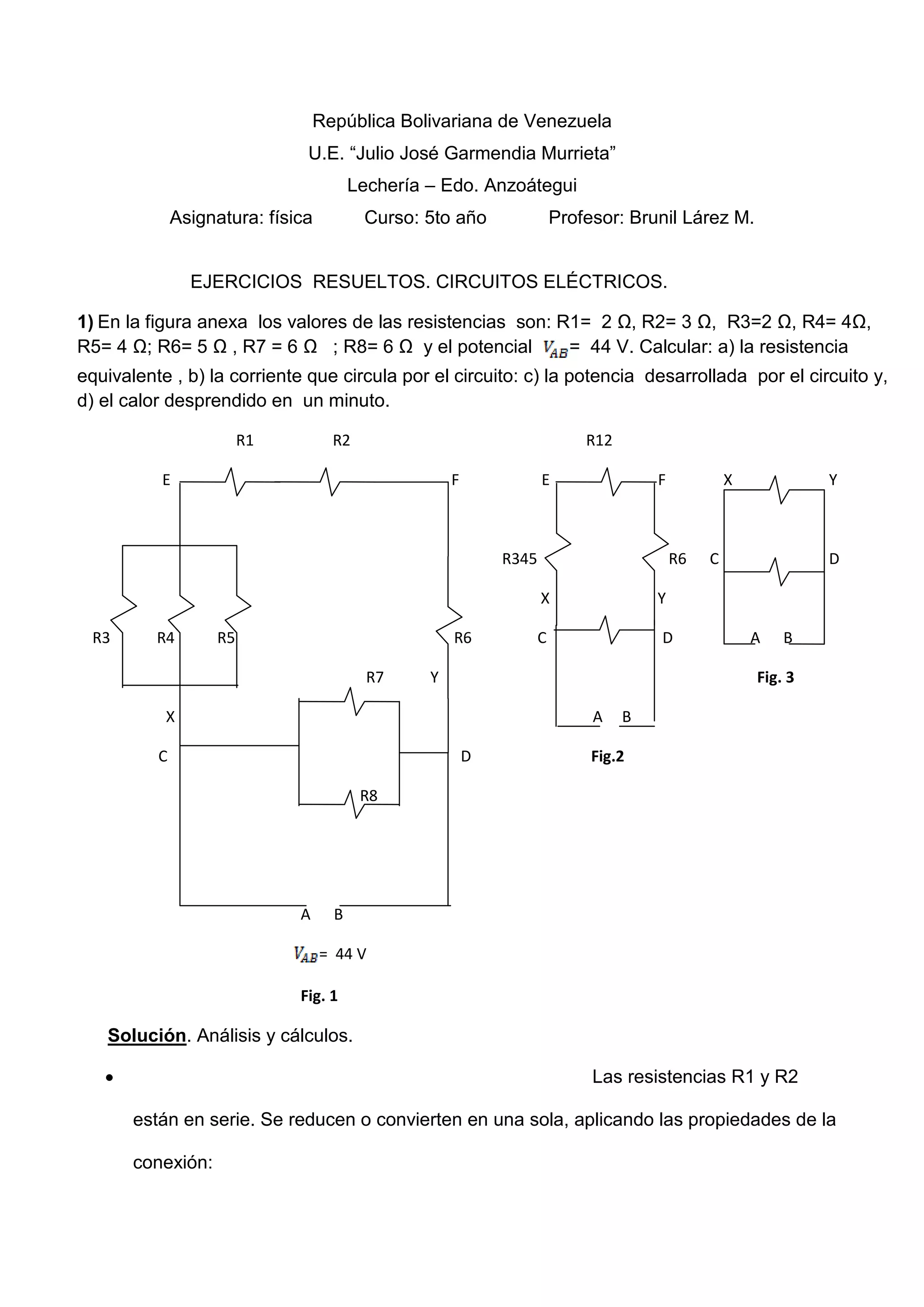
Este documento presenta la resolución de dos ejercicios de circuitos eléctricos. En el primer ejercicio, se calcula la resistencia equivalente de un circuito, la corriente que circula, la potencia desarrollada y el calor desprendido. En el segundo ejercicio, se calcula la resistencia externa y la corriente que circula por el circuito luego de reducir las resistencias en serie y paralelo mediante transformaciones progresivas del circuito representado en figuras.

1. República Bolivariana de Venezuela
U.E. “Julio José Garmendia Murrieta”
Lechería – Edo. Anzoátegui
Asignatura: física Curso: 5to año Profesor: Brunil Lárez M.
EJERCICIOS RESUELTOS. CIRCUITOS ELÉCTRICOS.
1) En la figura anexa los valores de las resistencias son: R1= 2 Ω, R2= 3 Ω, R3=2 Ω, R4= 4Ω,
R5= 4 Ω; R6= 5 Ω , R7 = 6 Ω ; R8= 6 Ω y el potencial = 44 V. Calcular: a) la resistencia
equivalente , b) la corriente que circula por el circuito: c) la potencia desarrollada por el circuito y,
d) el calor desprendido en un minuto.
R1 R2 R12
E F E F X Y
R345 R6 C D
X Y
R3 R4 R5 R6 C D A B
R7 Y Fig. 3
X A B
C D Fig.2
R8
A B
= 44 V
Fig. 1
Solución. Análisis y cálculos.
• Las resistencias R1 y R2
están en serie. Se reducen o convierten en una sola, aplicando las propiedades de la
conexión:

2. R12= R1+R2=2 Ω +3 Ω =5 Ω = Ω
• Las resistencias R7 y R8
están en paralelo. Deben convertirse en una sola, aplicando las propiedades de la
conexión:
Invertimos las fracciones y obtenemos: = = 3 Ω
• Las resistencias R3, R4 y R5
están en paralelo. Se convierten en una sola:
= 1 Ω
Obsérvese la Fig.2. Ahora las resistencias , R12 y R6 están en serie; se reducen a
una sola, llamada . = +R6= 1 Ω + 5 Ω + 5 Ω=11 Ω
Obsérvese la Fig.3. Ahora las resistencias y están en paralelo; se reducen
a una sola, llamada. Rt.
= Rt= Ω
Respuestas: a) Rt= Ω
b) I= aplicando la ley de Ohm; I= =26 A
c) P=V.I= 44V. 26 A=1144 W
d) Q=0,24. cal
Q=0.24.
Q= 16473,6 Cal

3. El alumno plantearse y calcular la corriente que pasa por una resistencia en
particular, por ejemplo R3 ó R7; y calcular la potencia o la cantidad de calor en
alguna de las resistencias en particular.
R1 R2
2) E B C
ε=66 V R3 R4 R5
Ri R6
F R8 A X R7 D
Fig. 1
En la figura anterior la resistencia interna de la fuente es Ri= 1Ω, la fuente es de ε= 66 V
R1= 3 Ω, R2= 3 Ω, R3= 10 Ω, R4= 6 Ω, R5=6 Ω , R6=2 Ω ; R7=4 Ω ; R8= 4 Calcular la
resistencia externa y la corriente que circula por el circuito.
SOLUCIÓN. ANÁLISIS Y CÁLCULOS.
Las resistencias R6 y R7 están en serie. Por lo tanto se reducen a una sola resistencia:
R67= R6+R7=2 Ω +4 Ω = 6 Ω. El circuito equivalente es mostrado en la Fig. 2
E R1 B R2 C
R3 R4 R5 R67
Ri
F R8 A X
Fig. 2

4. Luego, de la Fig. 2, R5 y R67 quedan en paralelo y se reducen a una sola:
NOTA: es recomendable generar varias figuras que indiquen la secuencia de los
cambios o transformaciones realizadas en el circuito.
E R1 B R2 C
R567
Ri R3 R4
X
R8 A
Fig. 3
Obsérvese en la Fig. 3 que R2 y R567 quedan en serie, y se reducen a una sola
resistencia que llamaremos R2567:
R2567=R2+R567= 3 Ω + 3 Ω = 6 Ω
R1 B
R3 R4 R2567
Ri
R8 A
Fig. 4
De la Fig. 4 se observa que R4 y R2567 están en paralelo, y se reducen a una sola
resistencia.

5. R42567= 3 Ω
Luego se puede observar en la Fig. 5 que las resistencias R1, R42567 y R8 están en
serie, se reducen a una sola resistencia.
R1
R3 R42567 R3 R1425678
Ri Ri
R8
FIg. 5 Fig. 6
R1425678=R1+R42567+R8; R1425678= 3 +3 4 =10
Luego, de la Fig. 6, se observa que las Resistencias R3 y R1425678, quedan en paralelo.
Aplicamos la propiedad de la conexión para calcular la resistencia externa del circuito:
= = , Re= 5 es la resistencia externa del circuito.
Respuesta
Una vez calculada la Re, se procede a calcular la intensidad de la corriente que circula por
el circuito. Para esto se aplica la ley de Ohm para un circuito completo:
Sustituyendo valores:
I= 66V/(5 +1 )

6. I= 11 A Intensidad de la corriente que recorre el circuito. Respuesta
OBSERVACIÓN GENERAL: para los efectos de enseñanza - aprendizaje el ejercicio se
realizó con múltiples figuras para señalar los cambios y cálculos intermedios realizados. En
los ejercicios el estudiante puede realizar varios cambios y cálculos simultáneos, siempre y
cuando esté claro de lo que desea calcular. Los ejercicios resueltos del libro también son de
utilidad.