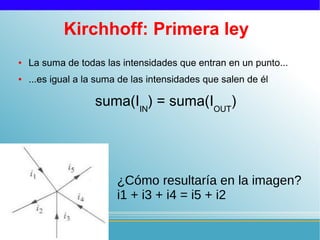
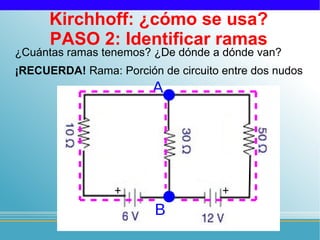
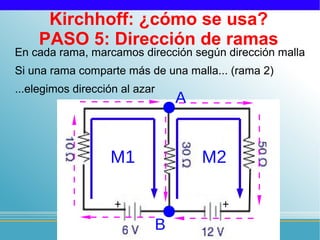
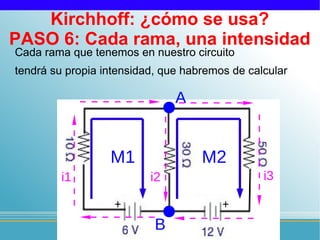
Las leyes de Kirchhoff establecen que: 1) la suma de intensidades que entran a un nudo es igual a la suma de las que salen, y 2) la suma de tensiones en un circuito cerrado es igual a la suma de caídas de tensión. El documento explica los 11 pasos para aplicar estas leyes y resolver circuitos eléctricos, incluyendo identificar nudos, ramas, mallas, direcciones, ecuaciones, y verificar la solución.

1. CFGM Instalaciones eléctricas y automáticas
Electrotecnia
Análisis de circuitos: Kirchoff

2. Kirchhoff: conceptos
● Nudo: Punto de conexión de tres o más conductores
– En la imagen, A, B, C y D son nudos
● Rama: Porción de circuito entre dos nudos
● Malla: Circuito cerrado formado por varias ramas

3. Kirchhoff: Primera ley
● La suma de todas las intensidades que entran en un punto...
● ...es igual a la suma de las intensidades que salen de él
suma(IIN) = suma(IOUT)
¿Cómo resultaría en la imagen?
i1 + i3 + i4 = i5 + i2

4. Kirchhoff: Segunda ley
● Se usa sobre circuitos cerrados
● Es decir, sobre mallas
suma(V) = suma(R·I)
● La suma de todas las tensiones...
● ...es igual a la suma de caídas de tensión

5. Kirchhoff: ¿cómo se usa?
Vamos a usar este circuito para ver cómo se usa:

6. Kirchhoff: ¿cómo se usa?
PASO 1: Identificar nudos
Marcamos los nudos que existen en el circuito
¡RECUERDA! Nudo: Conexión de tres o más conductores
A
B

7. Kirchhoff: ¿cómo se usa?
PASO 2: Identificar ramas
¿Cuántas ramas tenemos? ¿De dónde a dónde van?
¡RECUERDA! Rama: Porción de circuito entre dos nudos
A
B

8. Kirchhoff: ¿cómo se usa?
PASO 3: Identificar las mallas
¿Cuántas mallas hay? ¿Cuáles son?
¡RECUERDA! Malla: Circuito cerrado formado por varias ramas
A
M1 M2
B

9. Kirchhoff: ¿cómo se usa?
PASO 4: Dirección de mallas
En cada malla, marcamos dirección como agujas reloj
A
M1 M2
B

10. Kirchhoff: ¿cómo se usa?
PASO 5: Dirección de ramas
En cada rama, marcamos dirección según dirección malla
Si una rama comparte más de una malla... (rama 2)
...elegimos dirección al azar
A
M1 M2
B

11. Kirchhoff: ¿cómo se usa?
PASO 6: Cada rama, una intensidad
Cada rama que tenemos en nuestro circuito
tendrá su propia intensidad, que habremos de calcular
A
M1 M2
i1 i2 i3
B

12. Kirchhoff: ¿cómo se usa?
PASO 7: Ley 1 a los nodos
Aplicamos Ley 1 a los nodos del circuito
Pero no a todos:
- Si tenemos 4 mallas, a 3 nudos
- Si tenemos 3 mallas, a 2 nudos
- Si tenemos 2 mallas, a 1 nudo
- Si tenemos X mallas...
A
…a X – 1 nudos
En nuestro caso, 1 nudo M1 M2
RECUERDA i1 i2 i3
suma(IIN) = suma(IOUT)
B

13. Kirchhoff: ¿cómo se usa?
PASO 7: Ley 1 a los nodos
RECUERDA
suma(IIN) = suma(IOUT)
Elegimos nodo A
Daría igual si hubiéramos elegido el B
Entran:
i1 A
Salen:
i2, i3
Entonces tenemos:
M1 M2
i1 i2 i3
Ecuación 1
i1 = i2 + i3 B

14. Kirchhoff: ¿cómo se usa?
PASO 8: Ley 2 a las mallas
RECUERDA:
suma(V) = suma(R·I)
Empecemos por malla 1:
Solo tenemos un voltaje: de 6V
Tenemos dos intensidades: i1, i2
A
Tenemos dos resistencias:
de 10 y 30 ohmios
Entonces tenemos: M1
i1 i2
Ecuación 2
6 = 10·i1 + 30·i2
B

15. Kirchhoff: ¿cómo se usa?
PASO 8: Ley 2 a las mallas
RECUERDA: suma(V) = suma(R·I)
malla 2:
Solo tenemos un voltaje: de 12V
Voltaje va en dirección contraria a dirección de malla, será negativo
Tenemos dos intensidades: i2, i3
i2 también en dirección contraria A
Tenemos dos resistencias:
de 30 y 50 ohmios
Entonces tenemos:
M2
i2 i3
Ecuación 3
-12 = 50·i3 - 30·i2 B

16. Kirchhoff: ¿cómo se usa?
PASO 9: resolvemos ecuaciones
• Si tenemos 2 mallas, debemos tener 3 ecuaciones
• Si tenemos 3 mallas, 4 ecuaciones
• Si tenemos 4 mallas, 5 ecuaciones
• …
• Si tenemos X mallas, X + 1 ecuaciones

17. Kirchhoff: ¿cómo se usa?
PASO 9: resolvemos ecuaciones
• En nuestro caso, 2 mallas, luego 3 ecuaciones
Ecuación 1
i1 = i2 + i3
Ecuación 2
6 = 10·i1 + 30·i2
Ecuación 3
-12 = 50·i3 - 30·i2

18. Kirchhoff: ¿cómo se usa?
PASO 9: resolvemos ecuaciones
• Usamos ecuación 1 sobre ecuación 2
Ecuación 1
i1 = i2 + i3
Ecuación 2
6 = 10·i1 + 30·i2
En la ecuación 2, donde pone i1, ponemos i2 + i3:
6 = 10·(i2 + i3) + 30·i2 → 6 = 10·i2 + 10·i3 + 30·i2 →
6 = 40·i2 + 10·i3 → 6 – 10 i3 = 40 i2 →i2 = (6 – 10i3) / 40

19. Kirchhoff: ¿cómo se usa?
PASO 9: resolvemos ecuaciones
• Usamos ecuación 1-2 sobre ecuación 3
Ecuación 3
-12 = 50·i3 - 30·i2
En la ecuación 3, donde pone i2, ponemos la 1-2:

20. Kirchhoff: ¿cómo se usa?
PASO 9: resolvemos ecuaciones
• Ahora ya sabemos que i3=-0,1304A
• Usamos este valor sobre la ecuación 1-2
Hemos obtenido que i2 = 0,1826A

21. Kirchhoff: ¿cómo se usa?
PASO 9: resolvemos ecuaciones
• Ahora ya sabemos que:
• i3=-0,1304A
• i2 = 0,1826A
• Podemos usar estos valores en la ecuación 1
Ecuación 1
i1 = i2 + i3
i1 = 0,1826 - 0,1304 → i1 = 0,0522A
i1 = 52,2mA

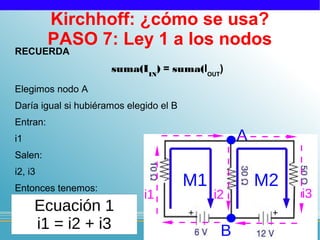
22. Kirchhoff: ¿cómo se usa?
PASO 10: Solución final
[EC1] i1 = i2 + i3
[EC2] 6 = 10·i1 + 30·i2
[EC3] -12 = 50·i3 - 30·i2
i1 = 0,0522A
i2 = 0,1826A
i3 = - 0,1304A

23. Kirchhoff: ¿cómo se usa?
PASO 11: Comprobar resultados
i1 = 0,0522A
i2 = 0,1826A
i3 = - 0,1304A
[EC1] i1 = i2 + i3
¿0,0522= 0,1826 – 0,1304?
0,0522= 0,0522 OK

24. Kirchhoff: ¿cómo se usa?
PASO 11: Comprobar resultados
i1 = 0,0522A
i2 = 0,1826A
i3 = - 0,1304A
[EC2] 6 = 10·i1 + 30·i2
¿6 = 10 · 0,0522 + 30 · 0,1826?
¿6 = 0,522 + 5,478?
6 = 6 OK

25. Kirchhoff: ¿cómo se usa?
PASO 11: Comprobar resultados
i1 = 0,0522A
i2 = 0,1826A
i3 = - 0,1304A
[EC3] -12 = 50·i3 - 30·i2
¿-12 = 50 · (-0,1304) - 30 · 0,1826?
¿-12 = -6,52 - 5,478?
-12 = -12 OK