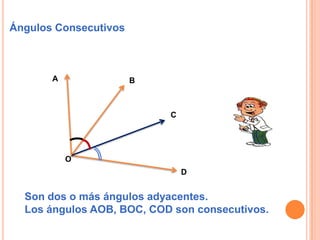
1) Un ángulo es la porción de plano comprendida entre dos semirrectas con un origen común. Se describen diferentes tipos de ángulos como adyacentes, consecutivos y complementarios/suplementarios. 2) Se explican conceptos como el complemento y suplemento de un ángulo. 3) Se presentan varios problemas relacionados al cálculo de medidas de ángulos utilizando las propiedades descritas.

2. Un ángulo es la porción de plano comprendida entre dos
semirrectas que tienen el origen común.
º
A
O
B

3. La bisectriz de un ángulo es la recta que pasando por el vértice
del ángulo lo divide en dos partes iguales.
A
B
O
m∢AOM = m∢MOB = º
M α
α

4. 0º < º < 90º º=90º 0º < º < 180º
º = 180º
º = 360º º =0º
°
°
°
°

5. Ángulos Adyacentes
B
A
C
O
Son dos ángulos que tienen el vértice y un lado común, el
lado común es intermedio.
Los ángulos AOB y BOC son adyacentes

6. Ángulos Consecutivos
BA
C
O
D
Son dos o más ángulos adyacentes.
Los ángulos AOB, BOC, COD son consecutivos.

7. Ángulos Opuesto por el vértice
A
C
B
D
O
Son dos ángulos en los cuales los lados de uno de
ellos, son las prolongaciones de los lados del otro, estos
dos ángulos son congruentes.
m∢AOB = m∢COD

8. Ángulos Complementarios
º
º
º + º = 90º
Son dos ángulos cuya suma es igual a 90

9. Ángulos Suplementarios
º + º = 180º
Son dos ángulos cuya suma es igual a 180
ºº

10. Complemento de un ángulo
C(º)=90 -  º
• Complemento de 38
El complemento de un ángulo es lo que le falta al ángulo
para ser igual a 90 .
• C(38 ) = 90 - 38 = 52
• C(42 ) = 90 - 42 = 48
• C(60 ) = 90 - 60 = 30

11. Suplemento de un ángulo
S(º)=180 -  º
• Suplemento de 38
El suplemento de un ángulo es lo que le falta al ángulo
para ser igual a 180 .
• S(70 ) = 180 -70 = 110
• S(50 ) = 180 - 50 = 130
• S(135 ) = 180 - 135 = 145

12. Observaciones
1. Cuando nos dicen “el complemento del complemento del
complemento del complemento del ........................... de un
ángulo que mide θ ”, tendremos:
N° par de veces N° impar de veces
135 veces
1486 veces

13. Observaciones
1. Cuando nos dicen “el complemento del complemento del
complemento del complemento del ........................... de un
ángulo que mide θ ”, tendremos:
N° par de veces N° impar de veces
85 veces
186 veces

14. Dado un ángulo agudo cuyo complemento es la cuarta parte de su
suplemento. Calcule la diferencia entre el suplemento de su doble
y su complemento.
PROBLEMA N° 1
SOLUCIÓN
Nos piden
• S(2x60°) - C(60°)
• (180° -120°) - (90° -60°)
• 60° - 30° = 30

15. El suplemento del complemento del suplemento de la medida de
un ángulo es igual a ocho veces la medida del ángulo. Encontrar el
suplemento del triple de la medida del ángulo.
PROBLEMA N° 2
SOLUCIÓN
SCS(θ)=8 θ Nos piden
180° - (90° -(180°- θ)))= 8θ
180° - (90° -180°+ θ)= 8θ
180° - 90° +180°- θ= 8θ
270° = 9θ
30° = θ
S(3θ) = S(90°)
180° - 90° = 90°

16. Dados dos ángulos agudos cuyas medidas son a y b tal que:
C(a) + C(b) = 140º y S(4a) – C(2a) = C(2b)
Calcular: S(5a)
PROBLEMA N° 3
SOLUCIÓN
• C(a) + C(b) = 140º
Nos piden
40° = a + a
a=20°
• 90° - a + 90° - b = 140º
• 180° - 140° = a + b
• 40° = a + b ……………(1)
• S(4a) – C(2a) = C(2b)
• (180° -4a) – (90° - 2a) = 90º -2b
• 180° -4a – 90° + 2a = 90º -2b
• 2b =2a
• a=b ………………(2)
(2) En (1)
S(5a) = 180° – 5a
180° – 5(20°)
180° – 100° = 80°

17. Se tiene un ángulo agudo cuya medida es a.
Calcule A/B si se sabe que:
3S(2a) – 2C(a) = AC(a)
3S(2a) + 2C(a) = BC(a).
PROBLEMA N° 4
SOLUCIÓN
3S(2a) – 2C(a) = AC(a)
3(180° -2a) – 2(90°-a)=A(90°-a)
540° -6a- 180° +2a = A(90°-a)
360° - 4a= A(90°-a)
4(90° - a)= A(90°-a)
A= 4
3S(2a) + 2C(a) = BC(a)
3(180° -2a) + 2(90°-a)=B(90°-a)
540° -6a+ 180° -2a = B(90°-a)
720° - 8a= B(90°-a)
8(90° - a)= B(90°-a)
B= 8

18. Se tienen los ángulos consecutivos AOB, BOC y COD tal que:
m ∡AOD = 6 m ∡ BOC y m ∡ AOB + m ∡ COD = 75 . Calcular m ∡ BOC
PROBLEMA N° 5
SOLUCIÓN
BA
C
O
D
a
b
c
• m ∡AOD = 6 m ∡ BOC
• a + b + c = 6b
• a + c = 5b ………(1)
• m ∡ AOB + m ∡ COD = 75
• a + c = 75 ……(2)
• 5b = 75
• b = 15

19. Se tienen los ángulos AOB, BOC y COD, consecutivos, tal que :
m∢AOD = 90º y m∢AOC + m∢BOD = 140º . Calcular : m∢BOC
PROBLEMA N° 6
SOLUCIÓN
BA
C
O
D
a
x
b
• m∢AOC + m∢BOD = 140º
• a + x + x + b = 140
• m∢AOD = 90º
• x + 90 = 140
• a + x + b = 90
• x = 50

20. Se tiene los ángulos consecutivos AOB, BOC, COD , se cumple quela m∡AOC
= m ∡ BOD=90°.Hallar la medida del ángulo formado por las bisectrices de los ángulos
AOB y COD
PROBLEMA N° 7
SOLUCIÓN
B
A
C
O
D
a
b
c
• m∡AOC = m ∡ BOD=90°.
• 2a + b = 90
• 2a + 2b+2c = 180
• a + b+ c = 90
• x= a+b+c
a
c
• b + 2c = 90
• Nos piden

21. Se tiene los ángulos consecutivos AOB, BOC, COD , de tal forma que
las bisectrices de los ángulos AOB y COD forman un ángulo de 90° y
m ∡ BOD=80°. Hallar m ∡ AOC.
PROBLEMA N° 8
SOLUCIÓN
BA
C
O
D
a
b
c
• m∡MON°= 90°
• a +b + c = 90
• m ∡ BOD=80°
• b + 2c = 80
m ∡ AOC = 2a +b
a
c
• Nos piden
M
N
• -2a -2b -2 c = -180
+
• -2a -b = -100
• 2a + b = 100

22. En los ángulos consecutivos AOB y BOC, tenemos que AOB es
menor que BOC, si m ∡AOB +2m ∡BOC = 148°. Luego , se traza OE bisectriz
del ángulo AOB y OP bisectriz del ángulo EOC. Hallar la medida del ángulo EOP
PROBLEMA N° 11
SOLUCIÓN
BA
C
O
a
b
• m ∡AOB +2m ∡BOC = 148°
• 2a +2(b-a+b) = 148
a
b
• Nos piden
E
P
• ∡ EOP=b =37
• 4b=148°
• 2a +2b-2a+2b= 148
• b=37°

23. Se tiene los ángulos consecutivos AOB, BOC, COD , de modo que
m ∡ BOC=20° y m ∡ AOD =130°, Traza las bisectrices OM de l ∡ AOB y ON del
∡ COD. Luego , halla la medida del ángulo MON
PROBLEMA N° 12
SOLUCIÓN
BA
C
O
D
a
20°
c
• m ∡ AOD =130°,
• 2a +20 + 2c = 130
• 2a+2c = 110°
• a + c = 55
a
c
• Nos piden
M
N • ∡ MON=a + 20 +c

24. Se tienen los ángulos consecutivos AOB y BOC tenemos que m ∡AOB = m ∡
BOC + 34°. Luego, se traza OM, bisectriz del ángulo AOC. Calcular m ∡ MOB
PROBLEMA N° 13
SOLUCIÓN
MA
B
O C
a+34°
b
a
• OM, bisectriz del ángulo AOC
• a + 34 = a +b
• 34 = b

25. En los ángulos AOF; FOB; BOR y ROC , tenemos que OF y OR bisecan a los
ángulos AOB y BOC, además m ∡AOB +2m ∡BOC=132°.Hallar m ∡FOR
PROBLEMA N° 14
SOLUCIÓN
FA
B
O
C
a
a
b
• m ∡AOB +2m ∡BOC=132°.
• 2a + 2b = 132
• a + b = 66°
b
• Nos piden
R • ∡ FOR=a + b

26. En los ángulos consecutivos AOB, BOC, COD, DOE se cumple que m ∡
AOC = 60°, m ∡ BOE = 2m∡AOB, m ∡ DOE = 2m∡COD. Calcular la medida del
ángulo BOD.
PROBLEMA N° 15
SOLUCIÓN
BA
C
O
E
60°
a
• Del grafico
• 3b= 60 + 3a
2a
• Nos piden
D
• b=20 +a
• x= a+ 60° - b
b
2b
• -20° = a - b

27. De la figura calcular “x”
PROBLEMA N° 16
SOLUCIÓN
• 2a + x = 90° …….(1)
De la figura
• 31x + 31a= 13a+13x+1170°
• 18x +18a = 1170°
a
a
x
• x +a = 65° ………………(2)
• (1) –(2) a = 25° en (2)
• X+25 = 65°