Descargar como PDF, PPTX
Subido porElvis Sosa
Columas esbeltas
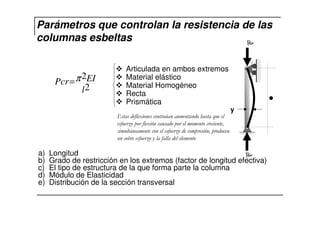
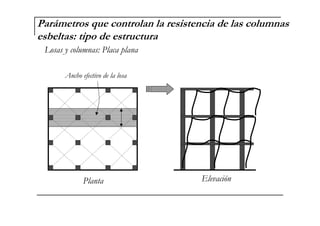
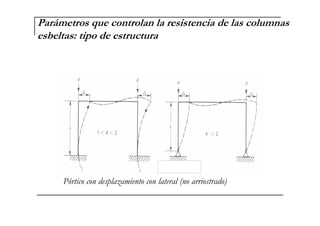
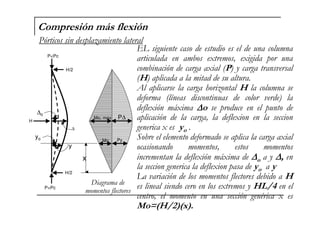
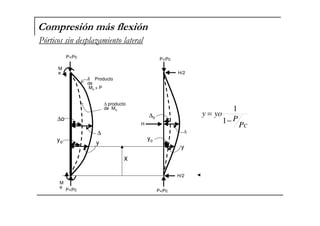
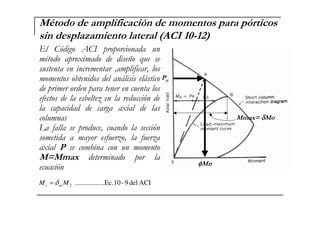
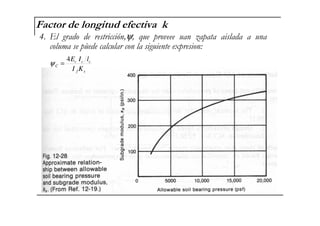
El documento describe las características de las columnas esbeltas y los métodos para calcular su resistencia. Explica que una columna es esbelta cuando sus dimensiones transversales son pequeñas en comparación con su longitud, lo que reduce su capacidad de carga debido a los momentos de segundo orden causados por la flexión. También cubre parámetros como la longitud, restricciones en los extremos, estructura, material y sección que controlan la resistencia, así como métodos en los códigos ACI para calcular la amplificación de momentos en pórticos con y
Más contenido relacionado
Columas esbeltas
- 1. COLUMNAS ESBELTAS Ing. CesarLeonidas Cancino Rodas Docente UPAO
- 2.
- 3. Contenido 1. ¿Columna esbelta? 2.Parámetros que controlan la resistencia de las columnas esbeltas 3. Columnas cargadas concéntrica mente que forman parte de marcos o pórticos sin desplazamiento lateral (arriostrados) 4. Columnas cargadas concéntrica mente que forman parte de marcos o pórticos con desplazamiento lateral (no arriostrados) 5. Compresión más flexión 6. Criterios del Código ACI para no tener en cuenta los efectos de esbeltez 7. Criterios del Código ACI para determinar cuando un pórtico esta arriostrado 8. Método de amplificación de momentos del Código ACI para pórticos arriostrados 9. Método de amplificación de momentos del Código ACI para pórticos no arriostrados
- 4. ¿Columna esbelta? Si lasdimensiones de la sección transversal son pequeñas en comparación con su longitud Son aquellas columnas cuya capacidad de carga axial (resistencia) se reduce debido a los momentos de segundo orden causados por la desviación lateral de la columna (pandeo). El Código ACI considera a una columna esbelta cuando su capacidad de carga axial se reduce en mas del 5% (¿ sección?)
- 5. Parámetros que controlanla resistencia de las columnas esbeltas a) Longitud b) Grado de restricción en los extremos (factor de longitud efectiva) c) El tipo de estructura de la que forma parte la columna d) Módulo de Elasticidad e) Distribución de la sección transversal 2 2 l EIPcr π= Articulada en ambos extremos Material elástico Material Homogéneo Recta Prismática y
- 7.
- 8. KL=0.5LKL=L KL=0.70L o: Centro dela curvatura K: factor de longitud efectiva KL: Longitud efectiva: Distancia entre los puntos de inflexión o o o Pi: Punto de inflexión o Punto de inflexión 2 2 = kl EIPcr π
- 9. Restricción parcial en losextremos L L/2<KL<L pi pi 2 2 = kl EIPcr π
- 10.
- 11. Restricción parcial en losextremos L L<KL< pi pi 2 2 = kl EIPcr π
- 13.
- 14.
- 15.
- 16.
- 17.
- 18. '() * +, ! - , , . /,//0, 1/3a 1/2 f`C
- 19.
- 20. 2 2 = kl EIPcr π ! ("2 , 3 $ & , " E c Ei Et # Ei: módulo tangente inicial (pendiente correspondiente al esfuerzo nulo) Ec: módulo secante (Pendiente de una recta secante a la curva, que une el punto de esfuerzo cero con otro cualquiera de la curva Et: módulo tangente (pendiente en cualquier punto de la curva) Deformación unitaria Esfuerzo F`c 0.50F`c
- 21. 2 2 = kl EIPcr π 12 3bh IX = b hX Y X Y 12 3bh IY= d X Y X Y 64 4d II YX π == X Y X Y ri re 64 44 −π == ie YX rr II A X I X r = A Y I Y r = bhA = 4 2 d A π = ( ) 4 22 ie rr A −π =
- 22. yo ∆o P<Pc P<Pc + = δ Productode Mo + P producto de Mo P<Pc Me Me P<Pc ∆ ∆o yo y Py P∆Me Diagrama de momentos flectores M=(P)(y) P<Pc yy ∆ P<Pc P<Pc Me Me Me Me !
- 23. & . $ 1&, " - ∆∆∆∆ , & " ∆∆∆∆ ∆∆∆∆ , . ! $ & # $ & ! 2 ! # , , . 2 45 !
- 24. H/2 H Mo,m ax P∆ M o Py P<Pc H/2 ∆o ∆ Mo, max Mo $ & $"&, " " $ 1 & ∆∆∆∆ , . ∆∆∆∆ ∆∆∆∆# " " $% - &"$'(&(! 6 x P<Pc yo y !
- 25. Pc P yoy − = 1 1 H/2 H P<Pc H/2 ∆o ∆ x P<Pc yo δ Producto de Mo +P ∆ producto de Mo P<Pc M e M e P<Pc ∆ ∆o yo y y !
- 26. ! ∆ # PcP PMPMMooo − ∆+=∆+= 1 1 max PcP MM o − = 1 1 max PcP−1 1 ) * ! !
- 27. Mo P∆ M Kl/r Mo MnM P Pc Pn " ! ! !
- 28. oM P<Pc P<Pc Me Me Py = + = eMeMM =max ó PyMM o +=max Pc P yoy 4 1 1 − = !
- 29.
- 30.
- 31. ', , " 0, ! &. & . , ), !
- 32. P P H P P , H Mo,max P Mp,max H+P Mmax += P P Mo,max Mp,max +
- 33.
- 34.
- 35.
- 36. . * / ), 0/,/8 cu ou lV P Q ∆ = 6 ΣΣΣΣ 1 , ∆∆∆∆ 9 , 2 - ΣΣΣΣ , 6 , 1 3
- 37. 4 * &+ ,-35-'( ACIdel9-10.......Ec...........2MMnsc δ= " : - ; δδδδ φφφφ
- 38. 4 * &+ ,-35-'( ACIdel10-10....Ec.....................0.1 75.0 1 ≥ − = c u m ns P P C δ () ACIdel11-10Ec..................................2 2 ukl EI Pc π = ( ) ACIdel13-10....Ec..................... 1 4.0 12-10Ec................... 1 20.0 d gc d sesgc IE EI IEIE EI β β + = + + = : - , : afactorizadtotalaxialcarga afactorizadpermanenteaxialcarga =dβ 6 * *
- 39. 4 * &+ ,-35-'( 14-10Ec............................4.60.0 2 1 += M M Cm , , ! ',/ '/<=#0 () 15-10Ec............................0300150min2 h..PM u, += 2 ,
- 40.
- 41. ) 7 ', ? @7 # ,
- 42. ) 7 0, $AB . ! & ( ) 0.105.085.0 0.105.070.0 min =≤+= ≤++= ψ ψψ BA k< & & , , " m m k ψ ψ + − = 1 20 20 ! 2<mψ ! 2≥mψ mk ψ+= 190.0 , C ψ3.00.2 +=k 8
- 43. ) 7 ), $@%, # % &< & & A '0<0 ,
- 44.