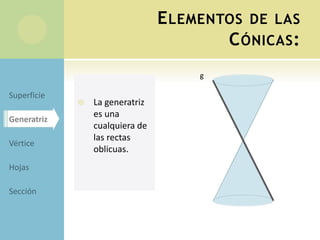
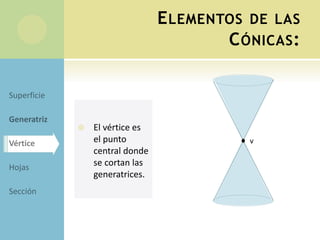
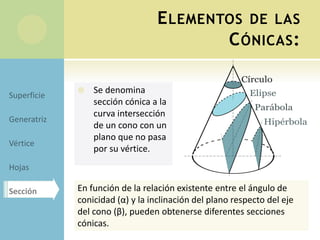
Este documento describe los elementos y ecuaciones de las principales secciones cónicas: la circunferencia, elipse, hipérbola y parábola. Define cada una de estas curvas como el lugar geométrico de puntos que cumplen cierta propiedad relacionada con la distancia a puntos fijos o rectas. Presenta las ecuaciones canónicas y reducidas de cada curva, así como conceptos como excentricidad, focos y vértices.

1. Profesora:
Castro, Gabriela SECCIONES CÓNICAS
Ciudad Guayana, Marzo de 2016
UNIVERSIDAD CATÓLICA ANDRÉS BELLO
FACULTAD DE INGENIERÍA
ESCUELA DE INGENIERÍA INDUSTRIAL
ASIGNATURA: CÁLCULO I

2. ELEMENTOS DE LAS
CÓNICAS:
 Una superficie
cónica de
revolución está
engendrada por la
rotación de una
recta alrededor de
otra recta fija,
llamada eje, a la
que corta de modo
oblicuo.

3. ELEMENTOS DE LAS
CÓNICAS:
 La generatriz
es una
cualquiera de
las rectas
oblicuas.
g

4. ELEMENTOS DE LAS
CÓNICAS:
 El vértice es
el punto
central donde
se cortan las
generatrices.
v

5. ELEMENTOS DE LAS
CÓNICAS:
 Las hojas son las
dos partes en las
que el vértice
divide a la
superficie cónica
de revolución.

6. ELEMENTOS DE LAS
CÓNICAS:
 Se denomina
sección cónica a la
curva intersección
de un cono con un
plano que no pasa
por su vértice.
En función de la relación existente entre el ángulo de
conicidad (α) y la inclinación del plano respecto del eje
del cono (β), pueden obtenerse diferentes secciones
cónicas.

7. SECCIONES CÓNICAS
http://www.rtve.es/aventur
a/mas-por-

8. LA CIRCUNFERENCIA
 Una circunferencia es el lugar geométrico
de los puntos P(x,y) que equidistas de un
punto fijo C llamado centro.
d(P,C)=r
 Sea P(x,y) un punto cualquiera verificando d(P,C)=r, siendo r
el radio y C(x0,Y0) el centro. De la fórmula de distancia de
dos punto se tiene
 Y elevando al cuadrado se obtiene la ecuación de la
circunferencia
 Cuando la circunferencia tiene centro en el origen se tiene
la ecuación reducida
𝑥 − 𝑥0
2 + 𝑦 − 𝑦0
2 = 𝑟
𝑥 − 𝑥0
2 + 𝑦 − 𝑦0
2 = 𝑟2
𝑥2
+ 𝑦2
= 𝑟2

9. RECTA TANGENTE A UNA
CIRCUNFERENCIA
 Si desde un punto P(x,y) trazamos una recta t, será
tangente a una circunferencia cuando la distancia del
centro a la recta coincida con el radio.
 La recta es tangente si
d(C,t)=radio
 La recta se llama exterior si
d=(C,t)>radio
 La recta se llama secante si
d=(C,t)<radio

10. LA ELIPSE
 Una elipse es el lugar geométrico de los P(x,y) cuya suma de distancias
a dos puntos fijos F y F’ (focos) es constante.
𝑃𝐹 + 𝑃𝐹′ = 2𝑎
 La ecuación reducida de una elipse cuando los ejes están situados en
el eje Ox y 𝑃𝐹 + 𝑃𝐹′ = 2𝑎 correspode a:
 a es el semieje mayor
 b es el semieje menor
 Focos F(c,0) y F’(-c,0)
 Vértices A, A’, B y B’
 En el gráfico se tiene :
 BF=a OB=b OC=c
𝑥2
𝑎2 +
𝑦2
𝑏2 = 1

11. LA ELIPSE
Excentricidad
 Llamamos excentricidad e de
una elipse al cociente entre la
distancia focal y el eje real
𝑒 =
𝑐
𝑎
=
𝑎2−𝑏2
𝑎
Cambio de centro
 La ecuación de la tangente
a la elipse en el punto P
es:
Ecuación de la tangente
 La ecuación de la elipse
cuando el centro esta en
el punto O(u,v) es:
𝑥 − 𝑢 2
𝑎2 +
𝑦 − 𝑣 2
𝑏2 = 1
𝑥0 𝑥
𝑎2 +
𝑦0 𝑦
𝑏2 = 1

12. LA HIPÉRBOLA
 Una hipérbola es el lugar geométrico de los P(x,y) cuya diferencia
de distancias a dos puntos fijos F y F’ (focos) es constante.
𝑃𝐹 − 𝑃𝐹′ = ±2𝑎
 La ecuación reducida de una Hipérbola cuando los ejes están
situados en el eje Ox y 𝑃𝐹 − 𝑃𝐹′
= ±2𝑎 correspode a:
 a es el semieje mayor
 b es el semieje menor
 Focos F(c,0) y F’(-c,0)
 Vértices A, A’, B y B’
 B y B’ son los corte de la circunferencia con centro en A y radio
c
𝑥2
𝑎2 −
𝑦2
𝑏2 = 1

13. LA HIPÉRBOLA
Excentricidad
 Llamamos excentricidad e de
una hipérbola al cociente entre
la distancia focal y el eje real
𝑒 =
𝑐
𝑎
> 1
Cambio de centro
 La ecuación de la tangente
a la hipérbola en el punto
P es:
Ecuación de la tangente
 La ecuación de la
hipérbola cuando el
centro esta en el punto
O(u,v) es:
𝑥 − 𝑢 2
𝑎2 −
𝑦 − 𝑣 2
𝑏2 = 1
𝑥0 𝑥
𝑎2 −
𝑦0 𝑦
𝑏2 = 1

14. LA PARÁBOLA
 Una parábola es el lugar geométrico de los P(x,y) que equidistan de una
recta fija 𝛿(directriz) y de un punto fijo F(foco).
𝑃𝐹 = 𝑑(𝑃, 𝛿)
 La ecuación reducida de una Parábola cuando los ejes están situados en el
eje Ox y directriz δ = 𝑥 = −
𝑝
2
correspode a:
 La recta VF es el eje
 Foco F (p/2,0)
 El vertice es V(0,0)
 directriz δ = 𝑥 = −
𝑝
2
 𝑉𝐹 = −
𝑝
2
 Si trasladamos una parábola al vértice V(u,v) su ecuación, es:
𝑦2
= 2𝑝𝑥
𝑦 − 𝑢 2
= 2𝑝 𝑥 − 𝑣

15. REFERENCIAS
 Cónicas (2014), recuperado el 14/03/2016 de:
http://www.vitutor.com/geo/coni/f_1.html
 González, J. Las Cónicas (2004), recuperado el
14/03/2016 de:
http://personales.unican.es/gonzaleof/Ciencias_
1/conicas.pdf