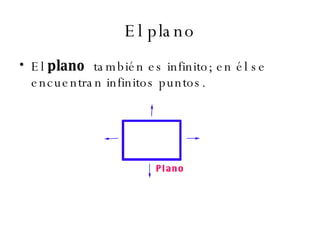
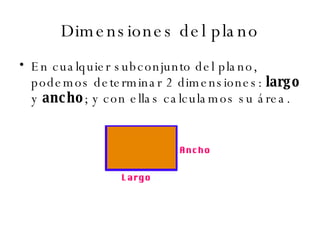
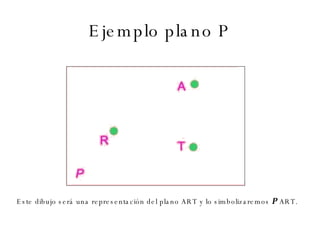
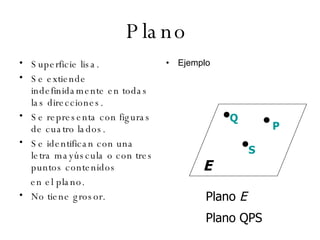
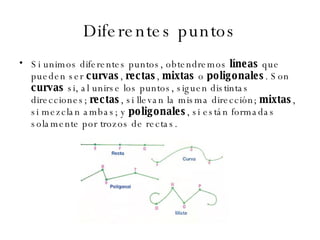
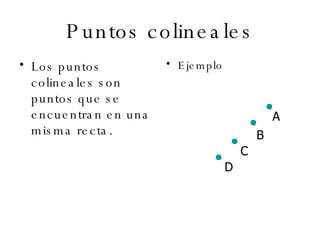
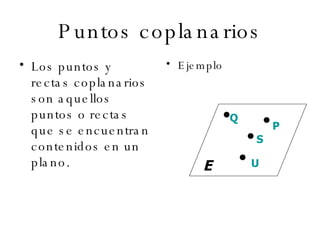
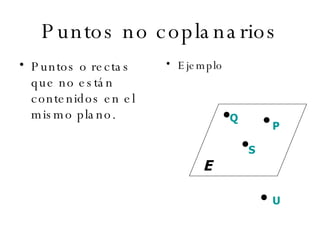
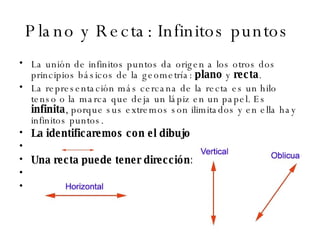
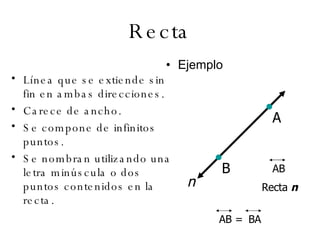
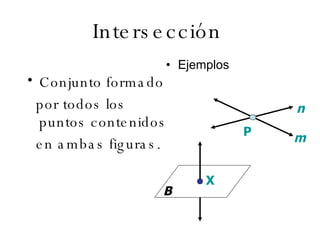
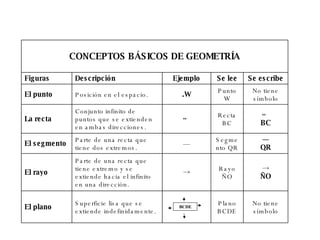
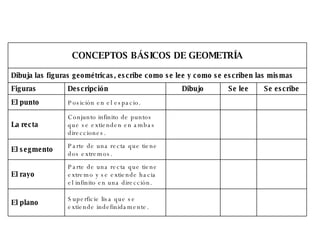
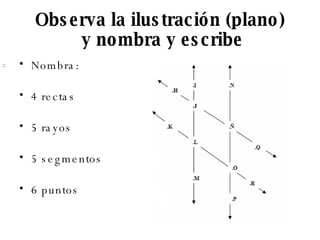
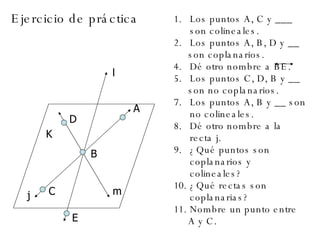
El documento describe los conceptos básicos de la geometría como el punto, la recta, el plano y sus propiedades. Explica que un punto no tiene tamaño y se representa con una letra mayúscula. Una recta está formada por puntos infinitos en una misma dirección. Un plano es una superficie infinita formada por puntos. También define conceptos como segmento, rayo, colineal y coplanario.

1. CONCEPTOS BÁSICOS DE GEOMETRÍA Actividad pedagógica Mathematics and Science Partnership: an experience in action research* http://www.icarito.cl/medio/articulo/0,0,38035857_152308921_191828175,00.html

2. Conceptos básicos de la geometría El punto, la recta y el plano son los conceptos básicos de la geometría. Se conocen como términos primitivos o no definidos.

3. El plano El plano también es infinito; en él se encuentran infinitos puntos.

4. Dimensiones del plano En cualquier subconjunto del plano, podemos determinar 2 dimensiones: largo y ancho ; y con ellas calculamos su área.

5. Plano Lo más parecido a este elemento del espacio es una hoja de papel, pero lo diferencia con ésta, el hecho que es ilimitado y no tiene grosor . El plano es una superficie infinita , formada por infinitos puntos que siguen una misma dirección, es decir, hay rectas que quedan totalmente incluidas en ella . El símbolo de plano es P y para nombrarlo debe estar acompañado de, por lo menos, tres puntos.

6. Ejemplo plano P Este dibujo será una representación del plano ART y lo simbolizaremos P ART.

7. Plano Superficie lisa. Se extiende indefinidamente en todas las direcciones. Se representa con figuras de cuatro lados. Se identifican con una letra mayúscula o con tres puntos contenidos en el plano. No tiene grosor. Ejemplo E Plano E Plano QPS Q S P

8. El plano en nuestro alrededor Las paredes de nuestra casa, el pavimento de las calles, la superficie de una laguna, son representaciones de planos. Es importante saber que en un plano podemos encontrar puntos y rectas , y obtener figuras geométricas . Hay planos horizontales , verticales y oblicuos . Cuando en una superficie no quedan rectas totalmente incluidas en ella, decimos que es curva . Una representación de esto sería una bandera flameando.

9. Espacio y punto Hay conceptos geométricos que no pueden definirse. Son ideas formadas en nuestra mente a través de la observación del entorno y solamente podemos hacer representaciones concretas de ellas. Las llamaremos términos primitivos o conceptos primarios y son: espacio , punto , recta y plano . http://www.eduteka.org/MI/master/interactivate/dictionary/Index.html

10. Punto El punto tiene posición en el espacio. Su representación más cercana es el orificio que deja un alfiler en una hoja de papel o en un granito de arena, pero debemos tener en cuenta que no tiene grosor. En el espacio hay infinitos puntos. Los identificaremos con una letra mayúscula y para reconocerlos usaremos o x. Por ejemplo: A se lee punto A, x M se lee punto M.

11. Punto Todas las figuras geométricas están formadas por puntos. Se representa con letras mayúsculas. No tiene tamaño. Es una localización. Ejemplo P Q R

12. Diferentes puntos Si unimos diferentes puntos, obtendremos líneas que pueden ser curvas , rectas , mixtas o poligonales . Son curvas si, al unirse los puntos, siguen distintas direcciones; rectas , si llevan la misma dirección; mixtas , si mezclan ambas; y poligonales , si están formadas solamente por trozos de rectas.

13. Puntos colineales Los puntos colineales son puntos que se encuentran en una misma recta. Ejemplo A B C D

14. Puntos no colineales No se encuentran contenidos en una recta . Ejemplo A B D

15. Puntos coplanarios Los puntos y rectas coplanarios son aquellos puntos o rectas que se encuentran contenidos en un plano. Ejemplo E Q S P U

16. Puntos no coplanarios Puntos o rectas que no están contenidos en el mismo plano. Ejemplo E Q S P U

17. Plano y Recta: Infinitos puntos La unión de infinitos puntos da origen a los otros dos principios básicos de la geometría: plano y recta . La representación más cercana de la recta es un hilo tenso o la marca que deja un lápiz en un papel. Es infinita , porque sus extremos son ilimitados y en ella hay infinitos puntos. La identificaremos con el dibujo Una recta puede tener dirección:

18. Rectas Cuando es distinta a las dos anteriores. Las rectas se nombran con dos letras mayúsculas y sobre ellas se anota su símbolo. Por ejemplo: , se lee recta AB. También se usa una L ó una R, especialmente en los casos en que deban distinguirse varias rectas. Veamos: L es una recta vertical.

19. Recta La recta ( ) está formada por infinitos puntos que siguen una misma dirección: horizontal, vertical u oblicua. “ Una recta puede prolongarse en ambas direcciones ”. “ Por dos puntos dados puede hacerse pasar una sola recta ”.

20. Segmento Un subconjunto de la recta es el segmento o trazo ( ). Este tiene limitados sus 2 extremos, lo que hace posible medir su longitud.

21. Segmento El segmento o es la parte de la recta que contiene los puntos A y B, así como los puntos de la recta que están entre A y B. A los puntos A y B se les llama extremos del segmento La longitud o medida de es la distancia entre los puntos A y B. El simbolo significa la longitud de A a B.

22. Rayo El rayo es la parte de la recta que está formada por A y todos los puntos que están del mismo lado de B. Al punto A se le llama punto inicial del rayo. Se dice que dos rayos son opuestos si están en la misma recta y tienen un punto común. En la figura 2 , es opuesto a y tiene el punto común X.

23. Recta Línea que se extiende sin fin en ambas direcciones. Carece de ancho. Se compone de infinitos puntos. Se nombran utilizando una letra minúscula o dos puntos contenidos en la recta. Ejemplo n Recta n = A B AB AB BA

24. Intersección Conjunto formado por todos los puntos contenidos en ambas figuras. Ejemplos m n B P X

25. BCDE No tiene símbolo Plano BCDE Superficie lisa que se extiende indefinidamente. El plano -> ÑO Rayo ÑO -> Parte de una recta que tiene extremo y se extiende hacia el infinito en una dirección. El rayo — QR Segmento QR — Parte de una recta que tiene dos extremos. El segmento ↔ BC Recta BC ↔ Conjunto infinito de puntos que se extienden en ambas direcciones. La recta No tiene símbolo Punto W .W Posición en el espacio. El punto Se escribe Se lee Ejemplo Descripción Figuras CONCEPTOS BÁSICOS DE GEOMETRÍA

26. CONCEPTOS BÁSICOS DE GEOMETRÍA Superficie lisa que se extiende indefinidamente. El plano Parte de una recta que tiene extremo y se extiende hacia el infinito en una dirección. El rayo Parte de una recta que tiene dos extremos. El segmento Conjunto infinito de puntos que se extienden en ambas direcciones. La recta Posición en el espacio. El punto Se escribe Se lee Dibujo Descripción Figuras Dibuja las figuras geométricas, escribe como se lee y como se escriben las mismas

27. Observa la ilustración (plano) y nombra y escribe Nombra: 4 rectas 5 rayos 5 segmentos 6 puntos :

28. Ejercicio de práctica l A C B D m j E K Los puntos A, C y ___ son colineales. Los puntos A, B, D y __ son coplanarios. Dé otro nombre a BE. Los puntos C, D, B y __ son no coplanarios. Los puntos A, B y __ son no colineales. Dé otro nombre a la recta j. ¿Qué puntos son coplanarios y colineales? ¿Qué rectas son coplanarias? Nombre un punto entre A y C.

29. Dibuje un diagrama para cada descripción. Rotule el diagrama. 1. El punto P está contenido en dos rectas. 2. Los puntos A, Q y S son coplanarios. 3. El punto M no está contenido en la recta l. 4. La recta t contiene los puntos Q y R, pero no contiene el punto P ni el S. 5. El plano K contiene los puntos A, B y C pero no contiene el punto D. 6. El punto X está entre A y B y A está entre X y Y. 7. La recta m interseca a DE en el punto F de tal manera que E está entre D y F.