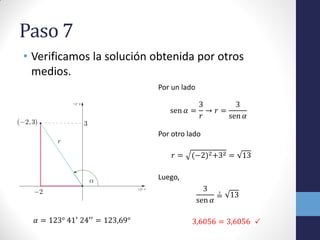
Este documento describe los pasos para hallar el valor de un ángulo en el segundo cuadrante dado las coordenadas de un punto. Primero se identifican los datos y se relacionan con la función tangente. Luego se despeja el ángulo y se obtiene un valor inicial. Sin embargo, este valor corresponde al cuarto cuadrante, por lo que se pasa el ángulo al segundo cuadrante restando del 180°. Finalmente, se verifica la solución obtenida mediante otras fórmulas. El ángulo buscado es de 123° 41'

1. Hallando un ángulo en
el segundo cuadrante
UNPSJB
Ms. Ana María Teresa Lucca

2. Problema
• Hallar el valor del
ángulo en posición
estándar cuyo lado
final contiene al
punto de
coordenadas
(-2, 3).

3. Paso 1
• Identificamos claramente los datos del
problema.

4. Paso 2
• Los datos se relacionan con la función tangente.
tg 𝛼 =
3
−2

5. Paso 3
• Despejamos el ángulo.
tg 𝛼 =
3
−2
𝛼 = arc tg −
3
2

6. Paso 4
• Con la calculadora obtenemos el valor del
ángulo en grados decimales.
𝛼 = −56,309932°
tg 𝛼 =
3
−2
𝛼 = arc tg −
3
2

7. Paso 5
• Pasamos el ángulo obtenido a GMS.
𝛼 = −56° 18′
36′′
𝛼 = −56,309932°
tg 𝛼 =
3
−2
𝛼 = arc tg −
3
2

8. Atención
• El ángulo  que buscamos
pertenece al segundo
cuadrante, es decir que
debe verificar:
90° <  < 180°
• Con la calculadora hemos
encontrado el valor
 = -56° 18’ 36’’ que
corresponde a un ángulo
en el cuarto cuadrante.

9. Paso 6
• Determinar el valor adecuado del ángulo, en el
segundo cuadrante.
𝛼 = 180° − 56° 18′
36′′
𝜶 = 𝟏𝟐𝟑° 𝟒𝟏′ 𝟐𝟒′′

10. Paso 7
• Verificamos la solución obtenida por otros
medios.
𝛼 = 123° 41′
24′′
= 123,69°

11. Paso 7
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
Por un lado
𝛼 = 123° 41′
24′′
= 123,69°

12. Paso 7
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
𝑟 = (−2)2+32 = 13
Por un lado
Por otro lado
𝛼 = 123° 41′
24′′
= 123,69°

13. Paso 7
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
Por un lado
Por otro lado
3
sen 𝛼
≟ 13
Luego,
𝛼 = 123° 41′
24′′
= 123,69°
𝑟 = (−2)2+32 = 13

14. Paso 7
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
Por un lado
Por otro lado
3
sen 𝛼
≟ 13
3,6056 = 3,6056 
Luego,
𝛼 = 123° 41′
24′′
= 123,69°
𝑟 = (−2)2+32 = 13

15. Paso 8
• Respuesta:
El ángulo  = 123° 41’ 24’’
en posición estándar contiene en su lado final
al punto de coordenadas (-2, 3).
Observación: El ángulo obtenido con la calculadora
no pertenecía al segundo cuadrante (90° <  < 180°)
y resultó necesario pasarlo a él.

16. Fin de la presentación