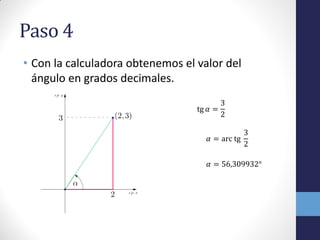
El documento describe los pasos para hallar el valor de un ángulo en el primer cuadrante cuando se conoce el punto (2,3) en sus coordenadas. Primero se identifican los datos del problema y se relacionan con la función tangente. Luego se despeja el ángulo y con una calculadora se obtiene el valor en grados decimales de 56.309932°, el cual se pasa a grados, minutos y segundos. Finalmente, se verifica la solución obtenida.

1. Hallando un ángulo en
el primer cuadrante
UNPSJB
Ms. Ana María Teresa Lucca

2. Problema
• Hallar el valor del
ángulo en posición
estándar cuyo lado
final contiene al
punto de
coordenadas
(2, 3).

3. Paso 1
• Identificamos claramente los datos del
problema.

4. Paso 2
• Los datos se relacionan con la función tangente.
tg 𝛼 =
3
2

5. Paso 3
• Despejamos el ángulo.
tg 𝛼 =
3
2
𝛼 = arc tg
3
2

6. Paso 4
• Con la calculadora obtenemos el valor del
ángulo en grados decimales.
tg 𝛼 =
3
2
𝛼 = arc tg
3
2
𝛼 = 56,309932°

7. Paso 5
• Pasamos el ángulo obtenido a GMS.
tg 𝛼 =
3
2
𝛼 = arc tg
3
2
𝛼 = 56,309932°
𝛼 = 56° 18′
36′′

8. Paso 6
• Verificamos la solución obtenida por otros
medios.
𝛼 = 56° 18′
36′′
= 56,309932°

9. Paso 6
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
𝛼 = 56° 18′
36′′
= 56,309932°
Por un lado

10. Paso 6
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
𝛼 = 56° 18′
36′′
= 56,309932°
𝑟 = 22 + 32 = 13
Por un lado
Por otro lado

11. Paso 6
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
𝛼 = 56° 18′
36′′
= 56,309932°
𝑟 = 22 + 32 = 13
Por un lado
Por otro lado
3
sen 𝛼
≟ 13
Luego,

12. Paso 6
• Verificamos la solución obtenida por otros
medios.
sen 𝛼 =
3
𝑟
→ 𝑟 =
3
sen 𝛼
𝛼 = 56° 18′
36′′
= 56,309932°
𝑟 = 22 + 32 = 13
Por un lado
Por otro lado
3
sen 𝛼
≟ 13
3,6056 = 3,6056 
Luego,

13. Paso 7
• Respuesta:
El ángulo  = 56° 18’ 36’’
en posición estándar contiene en su lado final
al punto de coordenadas (2, 3).
Observación: el ángulo obtenido con la calculadora
pertenece al primer cuadrante (0 <  < 90°)
tal como pedía el problema.

14. Fin de la presentación