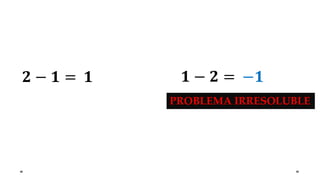
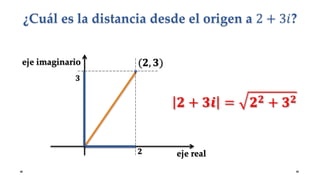
El documento describe la evolución del concepto de número a través de la historia, comenzando con los números racionales positivos en la antigua China, Egipto y Mesopotamia. Luego se detalla cómo los pitagóricos y Platón descubrieron los números irracionales, y cómo matemáticos posteriores como Brahmagupta, Descartes, y Euler extendieron el sistema numérico para incluir números negativos y complejos.

1. NÚMEROS
Ms. Ana María Teresa Lucca
Facultad de Ingeniería
Departamento de Matemática
matematicaconhistoria.jimdo.com

2. Extendiendo la idea de número

3. Número…
un concepto en evolución

4. Números racionales positivos
China Egipto Mesopotamia

5. Los números son fundamentales

6. en el lenguaje de la
GEOMETRÍA
Números…

7. Recta numérica real
𝟎 𝟏
escala
𝟐-1
Números positivosNúmeros negativos

8. 𝟎 𝟏 𝟐-1
Números positivosNúmeros negativos
Sólo miro para allá

9. • Partes de objetos• Objetos
Números

10. Números – objetos
enteros positivos

11. Números – objetos
1/2 kilo
fracciones positivas

12. Números racionales positivos
Para la mayoría sí,
pero…
matemáticamente

13. • Extracción de raíces• Suma
• Resta
• Multiplicación
• División
Operaciones aritméticas básicas

14. Los números racionales
positivos son cerrados bajo la
suma,
la multiplicación y la división.

15. 𝟐 − 𝟏 = 𝟏 𝟏 − 𝟐 = −𝟏
PROBLEMA IRRESOLUBLE

16. 𝟐
• Es positivo
• No es racional

17. −𝟐
Número “sin sentido”
𝟎

18. Sistema numérico
cerrado bajo la
aritmética básica
y la extracción
de raíces.

19. Números
irracionales

20. Un número irracional es un número
que no puede ser escrito como
un cociente de dos números enteros.

21. 4000 años atrás…
𝟐
algoritmo
recursivo
1
Aproximaciones
con números
racionales
Número
irracional
+
×
÷

22. Dados dos números,
siempre podemos
encontrar un
número racional
entre ellos.
Los números racionales son densos en la recta real.

23. Los números racionales son densos en la recta real.
No hay un intervalo que no contenga un número racional.
𝟐
número racional

24. • no buscaban una respuesta exacta
para 𝟐, se detenían cuando su
aproximación era suficientemente
buena para resolver su problema.
Los mesopotámicos…

25. Pitágoras de Samos

26. Pitágoras de Samos
(582 a.C. – 500 a.C.)
Números irracionales
𝟐

27. Los pitagóricos fueron los primeros en tomar
conocimiento de la existencia de
números que no son racionales.
Pitagóricos
Números que no pueden expresarse como
cociente de dos números enteros.

28. Todo es número.

29. Después de 𝟐…
𝟑
𝟕
𝟏𝟏

30. Aparte de descubrir lo que
los números irracionales no son,
los pitagóricos hicieron pocos avances
en el descubrimiento de lo que
los números irracionales son.

31. Platón
(427 a.C. – 347 a.C.)
𝟐 es irracional

32. 𝟐 es irracional
• Si 𝒂 𝟐
es divisible por 2,
entonces 𝒂 𝟐/𝟐 es par.
• Si 𝒃 𝟐 (o 𝒂 𝟐) es divisible por 2,
entonces 𝒃 (o 𝒂) es par.

33. En toda su historia, la mayoría de los matemáticos
se negaron a considerar soluciones irracionales
a problemas cuya solución dependía del cálculo.
Matemática griega

34. Diofanto
(Siglo III a.C.)

35. Números negativos

36. Números negativos
Varillas de conteo

37. • Utilizaba los números negativos como pasos
intermedios durante el curso de sus cálculos.
• No aceptaba a los números negativos como soluciones
definitivas a los problemas.
Matemática china

38. Matemática hindú

39. Brahmagupta
(598 – 655)
Observatorio astronómico de Ujjain

40. Brahmagupta
(598 – 655)
• Brahma Sphuta Siddhanta

41. • Explica cómo incorporar el cero y los números
negativos en la aritmética.
• Se hacen numerosas afirmaciones sin demostración
ni otros argumentos de apoyo.
• Todas las conclusiones están dadas en forma de una
serie de reglas.
Brahma Sphuta Siddhanta

42. Se amplía el conjunto de números
adaptándolo a los problemas a resolver,
en lugar de restringir los problemas a aquellos
con respuestas numéricas aceptadas.
Avance…

43. El menos es como tomar del mayor, positivo de positivo;
negativo de negativo. Cuando el mayor, sin embargo,
se resta del menor, la diferencia se invierte.
Negativo, tomado de cipher, se convierte en positivo; y
afirmativo (tomado de cipher), se convierte en negativo.
Negativo, menos cipher, es negativo; positivo (menos cipher),
es positivo; cipher (menos cipher), nada.
Brahmagupta

44. Brahmagupta

45. Positivo, dividido por positivo, o negativo por negativo,
es afirmativo. Cipher, dividido por cipher, es nada.
Positivo, dividido por negativo es negativo.
Negativo, dividido por afirmativo, es negativo.
Positivo, o negativo, dividido por cipher,
es una fracción con denominador.
Brahmagupta

46. Errores
𝟎
𝟎
= 𝟎
Positivo, o negativo,
dividido por cipher,
es una fracción con
denominador.

47. • Un número positivo dividido
por cero es igual a “infinito”.
• Si dividimos este mismo
número positivo por −𝟏,
debe ser “mayor que infinito”.
John Wallis
(1616 – 1703)

48. Números
algebraicos

49. Números negativos
como
soluciones
a ecuaciones
Albores del Renacimiento en Europa

50. René Descartes
(1596 – 1650)
Soluciones negativas - FALSAS
−𝟕

51. • Tratado de fluxiones - 1742
Los números negativos
representan un problema para
los matemáticos en cuanto a que
dan lugar a ideas que carecen de
cualquier base física.
Colin Maclaurin
(1698 – 1746)
Números negativos – un problema

52. Ecuaciones algebraicas
𝒂 𝒏 𝒙 𝒏
+ 𝒂 𝒏−𝟏 𝒙 𝒏−𝟏
+ ⋯ + 𝒂 𝟐 𝒙 𝟐
+ 𝒂 𝟏 𝒙 + 𝒂 𝟎 = 𝟎
potencias de la variable 𝒙
coeficientes  números racionales
grado de la ecuación

53. Un número que si se sustituye por 𝒙 en
se obtiene una declaración verdadera.
Solución de una ecuación algebraica
𝒂 𝒏 𝒙 𝒏 + 𝒂 𝒏−𝟏 𝒙 𝒏−𝟏 + ⋯ + 𝒂 𝟐 𝒙 𝟐 + 𝒂 𝟏 𝒙 + 𝒂 𝟎 = 𝟎

54. • Ecuación de grado 2
Ecuación cuadrática
𝒂 𝟐 𝒙 𝟐
+ 𝒂 𝟏 𝒙 + 𝒂 𝟎 = 𝟎
Ejemplo
𝒙 𝟐 + 𝒙 − 𝟐 = 𝟎
Una solución es 𝒙 = −𝟐
(−𝟐) 𝟐+ −𝟐 − 𝟐 = 𝟎

55. Un número que si se sustituye por 𝒙 en
se obtiene una declaración verdadera.
Solución de una ecuación algebraica
𝒂 𝒏 𝒙 𝒏 + 𝒂 𝒏−𝟏 𝒙 𝒏−𝟏 + ⋯ + 𝒂 𝟐 𝒙 𝟐 + 𝒂 𝟏 𝒙 + 𝒂 𝟎 = 𝟎
raíz de la ecuación algebraica

56. • Eran conocidas por…
… incluso algunas
de grado mayor.
Ecuaciones cuadráticas

57. Renacimiento - Italia
Ecuaciones
de tercer y
cuarto grado

58. Renacimiento - Italia
Ecuaciones
de tercer y
cuarto grado
nuevos
números
desafiaron su concepción
de número

59. Los números algebraicos
son aquellos que son soluciones
para ecuaciones algebraicas.
Números algebraicos

60. nuevos
números
algebraicos
nuevas
ecuaciones
algebraicas

61. Nuevos números algebraicos
Niccolò Fontana
Tartaglia
(1499 – 1557) Antonio María Fior
Ludovico Ferrari
(1522 – 1565)
Girolamo Cardano
(1501 – 1576)

62. Algoritmos de Tartaglia y Ferrari
Nuevo concepto de número
Para rescatar…

63. Para rescatar…
• Algunos de los números que surgieron como
soluciones a estas ecuaciones…
 no podían ser representados como longitudes de
segmentos de recta
 ni podían ser utilizados para identificar el número
de objetos en un conjunto.

64. Para rescatar…
• Aun no aceptando estos números como “reales”…
 podían ser manipulados de acuerdo con las
reglas de la aritmética.
 podían utilizarse para generar resultados
nuevos y válidos.
ficticios

65. • muestra al lector cómo manipular estos nuevos
números para encontrar nuevas soluciones
a problemas que antes no tenían solución.
• no cree que estos números tengan ninguna
utilidad práctica.
Cardano en su Ars Magna…

66. puede encontrar
dos números
cuya suma es 10 y
cuyo producto es 40.
Cardano demuestra que…

67. puede encontrar
dos números
cuya suma es 10 y
cuyo producto es 40.
Cardano demuestra que…
𝟓 + −𝟏𝟓
𝟓 − −𝟏𝟓
no pueden ser números reales

68. Así progresa la sutil
aritmética final la cual,
como se ha dicho, es tan
refinada como inútil.
Cardano

69. Los números racionales
positivos son cerrados bajo la
suma,
la multiplicación y la división.

70. Los números reales son
cerrados bajo la suma, la resta,
la multiplicación y la división.

71. −𝟐
Número “sin sentido”
𝟎

72. Sistema numérico
cerrado también
bajo la extracción
de raíces.

73. Números “ficticios”Números “reales”
Después de Tartaglia y Ferrari

74. • Invention nouvelle en l'algèbre
1629
Albert Girard
(1595 – 1632)
Concepción más amplia de número

75. • Concibe a los números negativos como distancias
dirigidas a lo largo de una recta.
• En sus soluciones a ecuaciones algebraicas utiliza
números positivos, negativos y complejos.
• Acepta todos estos números como raíces legítimas de
ecuaciones algebraicas.
Aportes de Girard

76. Relación entre una
ecuación algebraica y
sus raíces o soluciones.
Interés de Girard

77. Conclusión de Girard
Una ecuación algebraica
tiene tantas raíces
(soluciones) como
el grado de la ecuación.
Números negativos
Números complejos

78. • La Géométrie – 1637
René Descartes
Una ecuación algebraica no
puede tener más raíces
que el grado de la ecuación.
Números negativos
Números complejos

79. Oliver CromwellJohn Wallis
(1616 – 1703)

80. John Wallis
(1616 – 1703)
• The Keys to Mathematics
de William Oughtred
(1574 – 1660)

81. Representar
geométricamente
las raíces de ecuaciones
algebraicas cuadráticas
o de segundo grado.
Interés de Wallis

82. Wallis imaginó…
Números positivos
Números negativos
𝟎

83. Wallis imaginó a los
números complejos
que surgían como soluciones a
ecuaciones cuadráticas
como las dimensiones de
cuadrados con áreas negativas.

84. 𝟎
𝒂 + 𝒃 −𝟏
𝒂 + 𝒃 −𝟏

85. Gottfried Wilhelm Leibniz
(1646 – 1716)

86. Hemos demostrado el símbolo
−𝑎 como vacío de significado,
o más bien contradictorio y
absurdo. Sin embargo,
por medio de tales símbolos,
se establece que una parte del
álgebra es de gran utilidad.
Augustus De Morgan
(1806 – 1871)
Primera mitad del siglo XIX

87. Jacob Bernoulli
Nicolás II Daniel
Leonhard Paul Euler
(1707 – 1783)

88. • Fue el primero en utilizar la letra 𝑖 para −1.
• Estudió los logaritmos de los números negativos y
complejos.
• Estudió expresiones tales como 𝑎 + 𝑏𝑖 𝑐+𝑑𝑖.
Aportes de Euler a los complejos

89. Estudió el número con el
desarrollo decimal
2,71828…
Aportes de Euler a los complejos

90. Aportes de Euler a los complejos

91. • Aprendió cómo extender la definición de muchas
funciones que una vez se habían definido sólo para
números reales de manera que también se definieran
para números complejos arbitrarios.
Aportes de Euler a los complejos

92. Jean Le Rond d'Alembert
(1717 – 1783)

93. • Las consecuencias matemáticas de las tres leyes del
movimiento de Newton.
• Edición de una influyente enciclopedia.
Intereses de d’Alembert
Escribió la mayor parte
de los artículos de ciencia

94. El conjunto de los números
de la forma 𝑎 + 𝑏𝑖,
donde 𝑎 y 𝑏 representan números reales,
¿es "suficientemente grande"
para incluir todas las soluciones
a todas las ecuaciones algebraicas?
Intereses de d’Alembert

95. ¿Es el conjunto de números de la
forma 𝑎 + 𝑏𝑖 cerrado bajo las
operaciones aritméticas básicas:
suma, resta, multiplicación,
división y la extracción de raíces?

96. Demostración de d’Alembert Euler extiende el resultado
 Funciones logarítmicas
 Funciones trigonométricas
 Función exponencial

97. El sistema de los números complejos es la extensión mínima
del conjunto de los números racionales positivos
que es cerrada bajo cualquier combinación
de las operaciones matemáticas habituales.

98. ¿Cómo pueden ser
representados geométricamente
los números complejos?

99. 𝒂 + 𝒃 𝒊
parte real parte imaginaria
eje real
eje imaginario
(𝒂, 𝒃)

100. • Fue la primera persona que
tuvo la idea de representar
geométricamente los números
complejos.
Caspar Wessel
(1745 – 1818)

101. Jean Robert Argand
(1768 – 1822)
Diagrama de Argand

102. Carl Friedrich Gauss
(1777 – 1855)

103. ¿Cuál es la distancia de 3 y −3 al origen?
𝟎 𝟑−𝟑
𝟑 = −𝟑 = 𝟑
valor absoluto

104. ¿Cuál es la distancia desde el origen a 2 + 3𝑖?
eje real
eje imaginario (𝟐, 𝟑)
𝟐
𝟑
𝟐 + 𝟑𝒊 = 𝟐 𝟐 + 𝟑 𝟐

105. Funciones de una variable real
𝒚 = 𝒇(𝒙)
variables reales

106. Funciones de una variable compleja
𝒘 = 𝒇(𝒛)
variables complejas

107. Números
trascendentes
y la búsqueda de un sentido

108. Hay un número infinito
de números algebraicos.

109. • Cada número racional es un número algebraico.
𝒂 𝟎 racional
𝒙 − 𝒂 𝟎 = 𝟎

110. • Muchos números irracionales también son algebraicos.
𝟐 es irracional
𝒙 𝟐 − 𝟐 = 𝟎

111. La mayoría de los
números no son
algebraicos.

112. Los números que no son algebraicos
se llaman trascendentes o trascendentales.
Un número trascendente no es raíz
de ninguna ecuación algebraica.
Números trascendentes

113. Sospechas de su existencia…
Leonhard Paul Euler
número irracional

114. Johann Heinrich Lambert
(1728 – 1777)
𝝅 es irracional.

115. Adrien-Marie Legendre
(1752 – 1833)
Finales del siglo XVIII
𝝅 es trascendente.

116. Joseph Liouville
(1809 – 1882)
Existen números trascendentes

117. • Descubrimiento de un conjunto con un número
infinito de números trascendentes.
Aporte de Liouville

118. • Se coloca un 1 en la primera posición a la derecha del punto decimal
• Se coloca un 1 en el segundo lugar (2 = 2 × 1)
• Se coloca un 1 en el sexto lugar (6 = 3 × 2 × 1)
• Se coloca un 1 en el vigésimo cuarto lugar (24 = 4 × 3 × 2 × 1) …
0,11000100000000000000000100…
Ejemplo de número trascendente

119. Charles Hermite
(1822 – 1901)
𝒆 es trascendente.

120. Ferdinand von Lindemann
(1852 – 1939)
𝝅 es trascendente.

121. • no son racionales y no son la raíz de cualquier ecuación
algebraica.
• si escribimos el número como un decimal, nos
encontramos con que la secuencia de dígitos nunca
termina y nunca se forma un patrón que se repite.
• no tienen una notación conveniente.
Números trascendentes…

122. • Segunda mitad del siglo XX
fundamentos lógicos
Richard Dedekind
(1831 – 1916)

123. Los matemáticos estaban usando números
sin un conocimiento detallado
de su estructura lógica.
“todavía comprendían números irracionales por lo que no son”
Dedekind vio que…

124. • La definición rigurosa de la recta numérica real.
Aporte de Dedekind

125. Demostrar que el sistema numérico
también es continuo, y es continuo
de la misma manera que la recta es continua.
Objetivo de Dedekind

126. Encontrar una manera lógica de establecer
una correspondencia entre
los puntos de la recta y
el sistema de los números "reales“.
Necesitaba…

127. 𝒂

128. • El sistema numérico varía continuamente.
• No hay huecos.
• El sistema de los números complejos puede ser
imaginado como el conjunto de coordenadas en un
plano, donde ambos ejes real e imaginario son
completados a la manera de Dedekind.
Implicaciones de la idea

129. • Permite dar una respuesta positiva a preguntas tales
como:
¿Qué es 𝟐?
Implicaciones de la idea