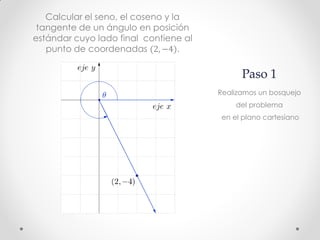
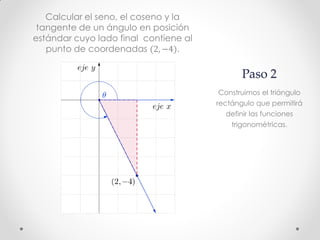
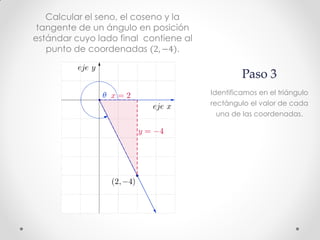
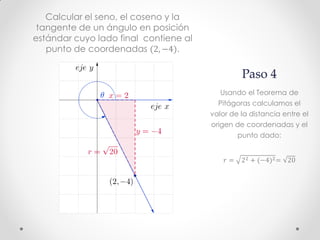
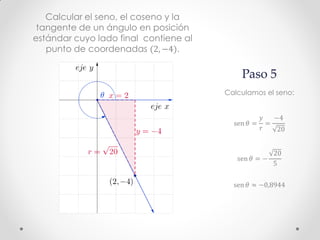
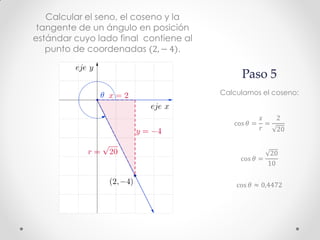
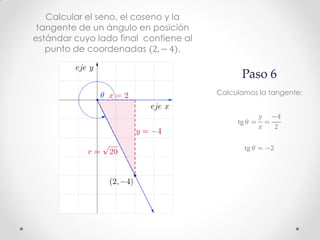
Este documento describe los pasos para calcular el seno, coseno y tangente de un ángulo en el cuarto cuadrante dado un punto. Primero se bosqueja el problema en un plano cartesiano y se construye un triángulo rectángulo. Luego, usando el Teorema de Pitágoras y las definiciones de seno, coseno y tangente, se calculan estas funciones trigonométricas para el punto (2, -4), obteniendo senθ ≈ -0.8944, cosθ ≈ 0.4472 y tgθ = -

1. Cálculo de funciones
trigonométricas de un
ángulo en el cuarto
cuadrante
UNPSJB
Ms. Ana María Teresa Lucca

2. Problema
Calcular el seno, el coseno y la tangente de un
ángulo en posición estándar cuyo lado final
contiene al punto de coordenadas (2, −4).

3. Paso 1
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, −4).
Realizamos un bosquejo
del problema
en el plano cartesiano

4. Paso 2
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, −4).
Construimos el triángulo
rectángulo que permitirá
definir las funciones
trigonométricas.

5. Paso 3
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, −4).
Identificamos en el triángulo
rectángulo el valor de cada
una de las coordenadas.

6. Paso 4
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, −4).
Usando el Teorema de
Pitágoras calculamos el
valor de la distancia entre el
origen de coordenadas y el
punto dado:
𝑟 = 22 + (−4)2= 20

7. Paso 5
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, −4).
Calculamos el seno:
sen 𝜃 =
𝑦
𝑟
=
−4
20
sen 𝜃 = −
20
5
sen 𝜃 ≈ −0,8944

8. Paso 5
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, − 4).
Calculamos el coseno:
cos 𝜃 =
𝑥
𝑟
=
2
20
cos 𝜃 =
20
10
cos 𝜃 ≈ 0,4472

9. Paso 6
Calcular el seno, el coseno y la
tangente de un ángulo en posición
estándar cuyo lado final contiene al
punto de coordenadas (2, − 4).
Calculamos la tangente:
tg 𝜃 =
𝑦
𝑥
=
−4
2
tg 𝜃 = −2

10. Resultados
Para un ángulo 𝜃 en posición estándar cuyo lado final
contiene al punto de coordenadas 2, − 4 tenemos:
sen 𝜃 = −
20
5
≈ −0,8944
cos 𝜃 =
20
10
≈ 0,4472
tg 𝜃 = −2

11. Observación
Para un ángulo en posición estándar
en el cuarto cuadrante:
El seno y la tangente son negativos.
El coseno es positivo.

12. Muchas gracias